初中数学人教版九年级下册28.1 锐角三角函数优秀ppt课件

这是一份初中数学人教版九年级下册28.1 锐角三角函数优秀ppt课件，共30页。PPT课件主要包含了素养目标，余弦的定义，正切的定义，想一想，可以大于1吗，sinA，cosA，tanA，锐角三角函数的定义，解由勾股定理得等内容，欢迎下载使用。
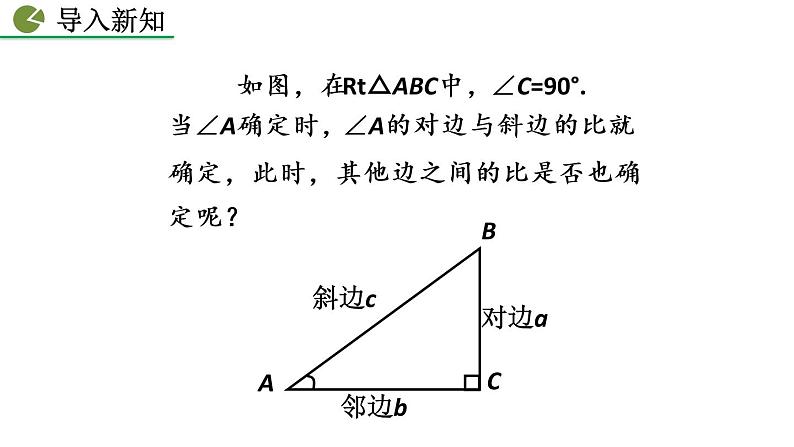
如图，在Rt△ABC中，∠C=90°.
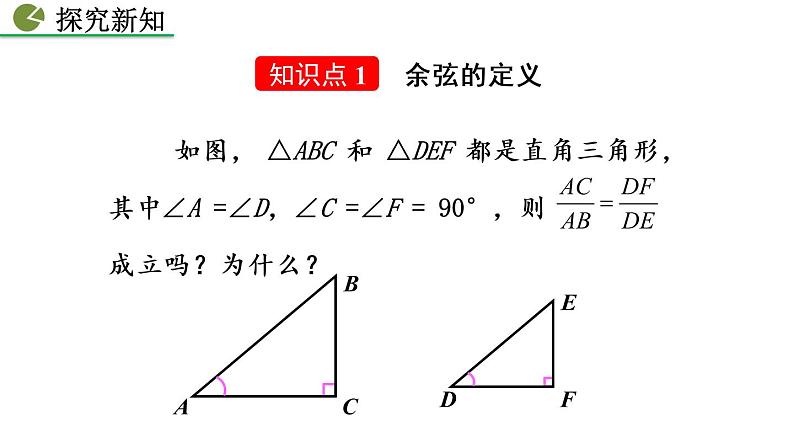
当∠A确定时，∠A的对边与斜边的比就确定，此时，其他边之间的比是否也确定呢？
2. 能灵活运用锐角三角函数进行相关运算.
1. 通过类比正弦函数，理解余弦函数、正切函数的定义，进而得到锐角三角函数的概念 .
3. 通过锐角三角函数的学习，培养学生类比学习的能力.
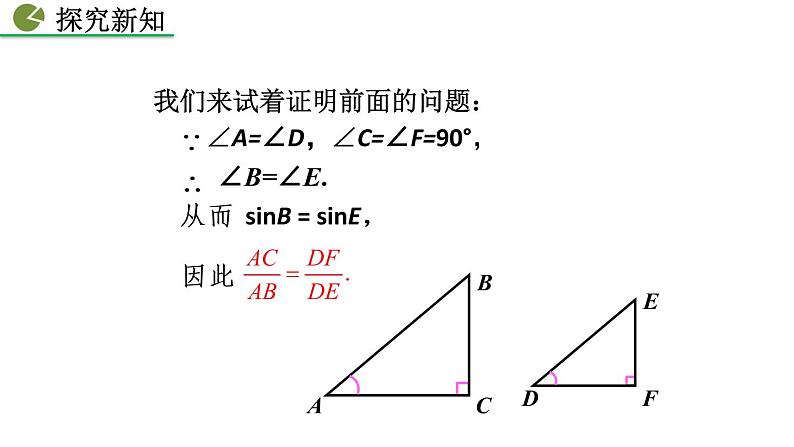
我们来试着证明前面的问题：
从而 sinB = sinE，
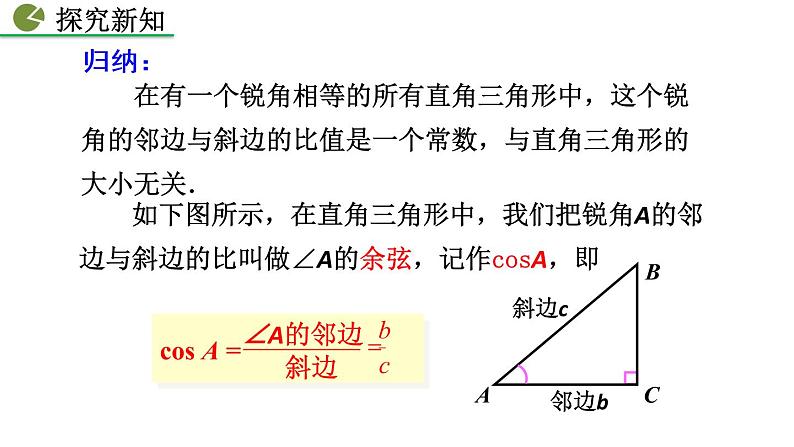
在有一个锐角相等的所有直角三角形中，这个锐角的邻边与斜边的比值是一个常数，与直角三角形的大小无关．
如下图所示，在直角三角形中，我们把锐角A的邻边与斜边的比叫做∠A的余弦，记作csA，即

从上述探究和证明过程，可以得到互余两角的三角函数之间的关系： 对于任意锐角α，有 cs α = sin (90°－ α),或sin α = cs(90°－ α).
1. sinA、csA是在直角三角形中定义的，∠A是锐角(注意数形结合，构造直角三角形). 2. sinA、 csA是一个比值（数值）. 3. sinA、 csA的大小只与∠A的大小有关，而与直角三角形的边长无关.
如图：在Rt △ABC中，∠C＝90°，
Rt△ABC中，∠C=90°，如果AB=2，BC=1，那么csB的值为（ ）
Rt△ABC中，∠C=90°，如果AC=4，BC=3，那么csB的值为_______.
证明：∵∠C=∠F=90°， ∠A=∠D， ∴Rt△ABC ∽ Rt△DEF.
如图：在Rt △ABC中，∠C＝90°，
我们把锐角A的对边与邻边的比叫做∠A的 正切，记作 tanA.
在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的对边与邻边的比是一个固定值.
1.如果两个角互余，那么这两个角的正切值有什么关系？
2.锐角A的正切值可以等于1吗？为什么？
在Rt∆ABC中，∠C＝90°，如果 那么tanB的值为（ ）
在Rt∆ABC中，∠C＝90°，如果 那么tanA的值为_______.
锐角A的正弦、余弦、和正切统称∠A的锐角三角函数.
脑中有“图”，心中有“式”
例1 如图，在 Rt△ABC 中，∠C=90°，AB=10，BC=6，求sinA，csA，tanA的值.
已知直角三角形两边求锐角三角函数的值
已知直角三角形中的两条边求锐角三角函数值的一般思路是：当所涉及的边是已知时，直接利用定义求锐角三角函数值；当所涉及的边是未知时，可考虑运用勾股定理的知识求得边的长度，然后根据定义求锐角三角函数值．
Rt△ABC中，∠C为直角，AC=5，BC=12，那么下列∠A的四个三角函数中正确的是( )
如图：P是∠ α的边OA上一点，且P点的坐标为（3，4），则csα______，tan α= ________.
已知一边及一锐角三角函数值求函数值
1. 如图，旗杆高AB=8m，某一时刻，旗杆影子长BC=16m，则tanC=______．
1. 在Rt△ABC中，∠C = 90°，AC = 12，AB =13. sinA=______，csA=______，tanA=____， sinB=______，csB=______，tanB=____.
2. 如图，△ABC 中一边 BC 与以 AC 为直径的 ⊙O相切与点 C，若 BC=4，AB=5，则 tanA=___.
3. 已知 ∠A，∠B 为锐角， (1) 若∠A =∠B，则 csA csB; (2) 若 tanA = tanB，则∠A ∠B; (3) 若 tanA · tanB = 1，则 ∠A 与 ∠B 的关系为： .
∠A +∠B = 90°
如图，在 Rt△ABC 中，∠ACB = 90°，CD⊥AB，垂足为 D. 若 AD = 6，CD = 8. 求 tanB 的值.
解: ∵ ∠ACB＝∠ADC =90°，
∴∠B+ ∠A=90°, ∠ACD+ ∠A =90°.
∴∠B = ∠ACD.
如图，在△ABC中，AB=AC=4，BC=6. 求csB 及 tanB 的值.
解：过点 A 作 AD⊥BC 于 D.
∵ AB = AC，
∴ BD = CD = 3，
在 Rt△ABD 中,
提示：求锐角的三角函数值问题，当图形中没有直角三角形时，可用恰当的方法构造直角三角形.