人教版九年级下册28.2 解直角三角形及其应用试讲课课件ppt

这是一份人教版九年级下册28.2 解直角三角形及其应用试讲课课件ppt，共26页。PPT课件主要包含了素养目标，解直角三角形的概念，在Rt△ABC中，一角一边，不能求其它元素，能求其它元素，解直角三角形的依据，解直角三角形的原则，知道两边解直角三角形，解根据勾股定理得等内容，欢迎下载使用。
要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所成的角α一般要满足50°≤ α ≤75°.现有一个长6m的梯子，问：（1）使用这个梯子最高可以安全攀上多高的墙（精确到0.1m）？（2）当梯子底端距离墙面2.4m时，梯子与地面所成的角α等于多少（精确到1°）？这时人能够安全使用这个梯子吗？
1. 了解解直角三角形的意义和条件.
2. 理解直角三角形中的五个元素之间的联系.
3. 能根据直角三角形中除直角以外的两个元素（至少有一个是边），解直角三角形.
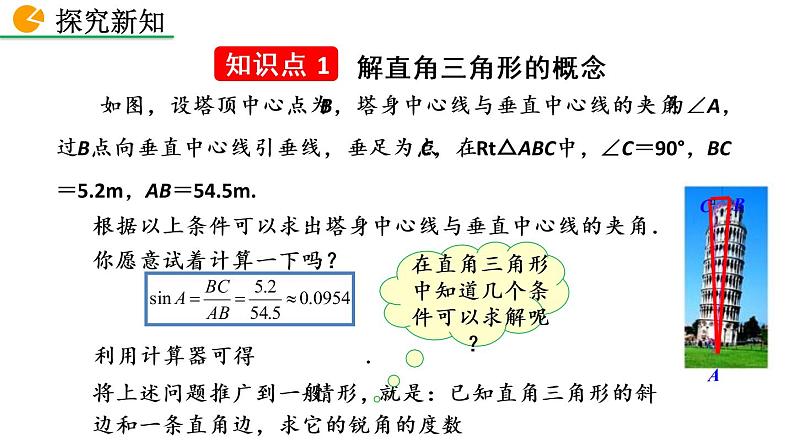
利用计算器可得 .
根据以上条件可以求出塔身中心线与垂直中心线的夹角．你愿意试着计算一下吗？
如图，设塔顶中心点为B，塔身中心线与垂直中心线的夹角为∠A，过B点向垂直中心线引垂线，垂足为点C，在Rt△ABC中，∠C＝90°，BC＝5.2m，AB＝54.5m.
将上述问题推广到一般情形，就是：已知直角三角形的斜边和一条直角边，求它的锐角的度数.
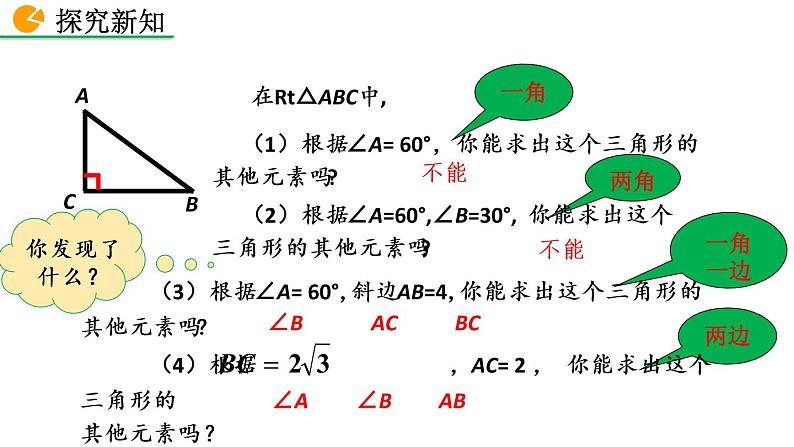
（2）根据∠A=60°,∠B=30°, 你能求出这个三角形的其他元素吗?
（1）根据∠A= 60°，你能求出这个三角形的其他元素吗?
（3）根据∠A= 60°,斜边AB=4,你能求出这个三角形的其他元素吗?
∠B AC BC
∠A ∠B AB
a2＋b2＝c2（勾股定理）；
(1)三边之间的关系:
(2)锐角之间的关系:
∠ A＋ ∠ B＝ 90º；
(3)边角之间的关系:
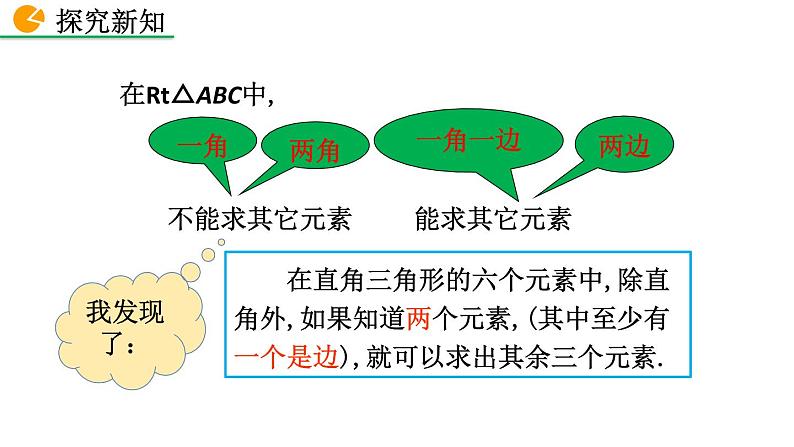
由直角三角形中的已知元素，求出其余未知元素的过程，叫作解直角三角形.

(1)有斜（斜边）用弦（正弦、余弦），无斜（斜边）用切（正切）；
(2)宁乘勿除：选取便于计算的关系式，若能用乘法计算就不用除法计算；
(3)取原避中：若能用原始数据计算，应避免使用中间数据求解.
如图，在Rt△ABC中，根据AC＝2.4，斜边AB＝6，你能求出这个直角三角形的其他元素吗？
在Rt△ABC中，∠C＝90°， a = 30 , b = 20,解这个直角三角形.
如图，在Rt△ABC中，根据∠A＝75°，斜边AB＝6，你能求出这个直角三角形的其他元素吗？
例 如图，在Rt△ABC中，∠C＝90°，∠B＝35°，b=20，解这个直角三角形 (结果保留小数点后一位).
在Rt△ABC,∠C=90°, ∠A=45°, c=4 解这个直角三角形.
∵ ∠A=45°，∴ ∠B=90°—∠A=45.
解：过点A作 AD⊥BC于D.在△ACD中，∠C=45°，AC=2，∴CD=AD= AC · sinC = 2sin45°= .在△ABD中，∠B=30°，
如图，在△ABC中，∠B=30°，∠C=45°，AC=2，求BC.
已知一边和三角函数值解直角三角形
在Rt△ABC中，∠C=90°，sinA = 0.8 ，BC=8，则AC的值为( )A．4 B．6 C．8 D．10
如图，在菱形ABCD中，AE⊥BC于点E，EC=4， ，则菱形的周长是 ( ) A．10 B．20 C．40 D．28
解：如图作CH⊥AB于H． 在Rt△BCH中，∵BC=12，∠B=30°，
1.在下列直角三角形中不能求解的是（ ）A.已知一直角边一锐角B.已知一斜边一锐角C.已知两边D.已知两角
2. 在Rt△ABC中，∠C=90°，∠B=37°，BC=32，则AC =______ (参考数据：sin37°≈0.60，cs37°≈0.80，tan37°≈0.75).
4. 在 Rt△ABC 中，∠C＝90°，∠B＝72°，c = 14. 根据条件解直角三角形.
如图，已知 AC = 4，求 AB 和 BC 的长．
分析：作CD⊥AB于点D，根据三角函数的定义，在Rt△ACD，Rt△CDB中，即可求出 CD，AD，BD 的长，从而求解．
在Rt△CDB中，∵∠DCB=∠ACB－∠ACD=45°，
解：如图，作CD⊥AB于点D，
在Rt△ACD中，∵∠A=30°，∴∠ACD=90°-∠A=60°.
∵ AD平分∠BAC，
∴∠CAD=30°.
∴∠CAB=60°, ∠B=30°,
解法：只要知道五个元素中的两个元素（至少有一个是边），就可以求出余下的三个未知元素.