




人教版九年级下册第二十八章 锐角三角函数28.2 解直角三角形及其应用优秀课件ppt
展开青青草原上,灰太狼每天都想着如何抓羊,而且屡败屡试,永不言弃.如图所示,一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=40 m,若灰太狼以 5 m/s的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果精确到个位)(假设懒洋洋不动)
1. 使学生了解仰角、俯角的概念,并能够根据直角三角形的知识解决实际问题.
2.在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路.
3. 进一步培养学生分析问题、解决问题的能力.
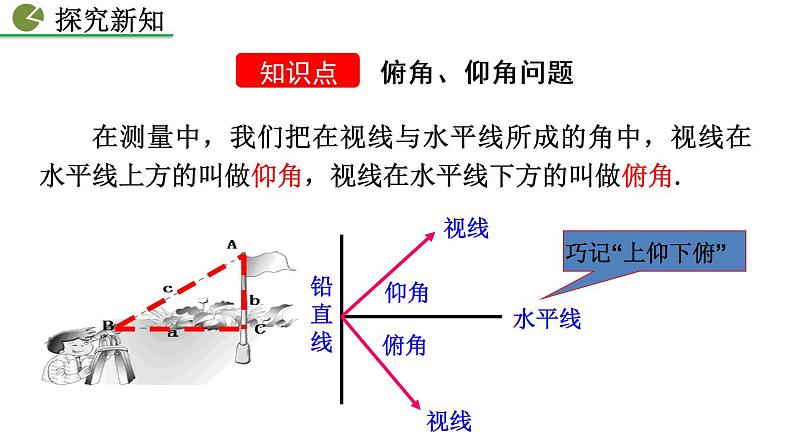
在测量中,我们把在视线与水平线所成的角中,视线在水平线上方的叫做仰角,视线在水平线下方的叫做俯角.
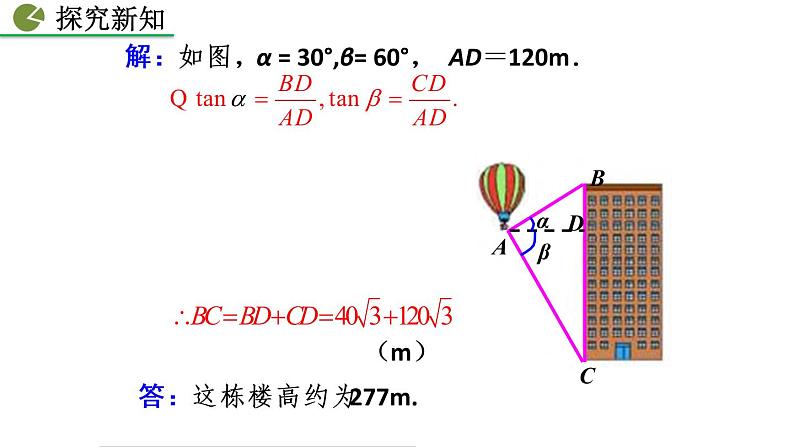
例1 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120m,这栋楼有多高(结果取整数)?
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.
在Rt△ABD中,α =30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
一个观测点构造两个直角三角形解答实际问题
解:如图,α = 30°,β= 60°, AD=120m.
答:这栋楼高约为277m.
解决与仰角、俯角有关的实际问题的方法
根据仰角、俯角的定义画出水平线、视线,找准仰角、俯角,结合题意,从实际问题情境中抽象出含仰角或俯角的直角三角形,然后利用解直角三角形使问题获解.
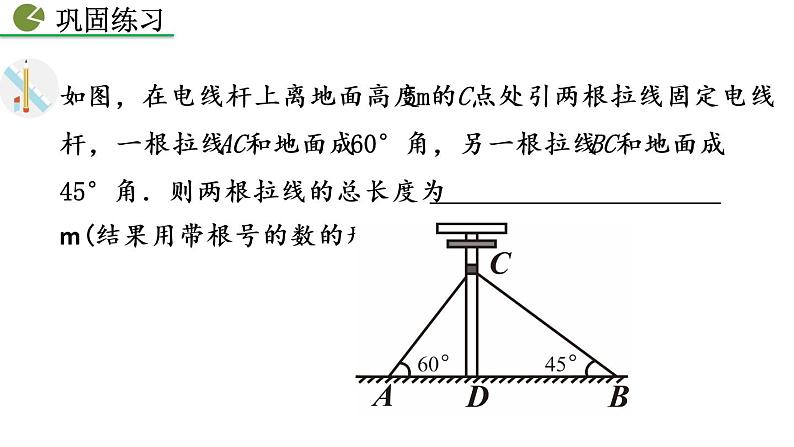
如图,在电线杆上离地面高度5m的C点处引两根拉线固定电线杆,一根拉线AC和地面成60°角,另一根拉线BC和地面成45°角.则两根拉线的总长度为 m(结果用带根号的数的形式表示).
例2 如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.6,cs37 °≈0.8,tan 37°≈0.75)
两个观测点构造两个直角三角形解答实际问题
在Rt△POB中,∠PBO=45°,
在Rt△POA中,∠PAB=37°,
解:作PO⊥AB交AB的延长线于O.
故飞机的高度为1200米.
如图,为了测出某塔CD的高度,在塔前的平地上选择一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.(1) 求点B到AD的距离;
答案:点B到AD的距离为20m.
(2) 求塔高CD(结果用根号表示).
解:在Rt△ABE中,∵∠A=30°,∴∠ABE=60°.∵∠DBC=75°,∴∠EBD=180°-60°-75°=45°.∴DE=EB=20m,则在Rt△ADC中,∠A=30°,答:塔高CD为 m.
如图,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上).为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为( )A. 800sinα米 B. 800tanα米 C. 米 D. 米
1. 如图①,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=____米.2. 如图②,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米.
3. 为测量松树AB的高度,一个人站在距松树15米的E处,测得仰角∠ACD=52°,已知人的高度是1.72米,则树高是 (精确到0.1米).
4. 如图,小明想测量塔AB的高度.他在D处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至C处.测得仰角为60°,小明的身高1.5 m.那么该塔有多高?(结果精确到1 m),你能帮小明算出该塔有多高吗?
解:由题意可知,∠AD′B′=30°,∠AC′B′=60°,D′C′=50m.
∴D′B′=x·tan60°,C′B′=x·tan30°,
∴x·tan60°-x·tan30°=50,
∴ ∠D′AB′=60°,∠C′AB′=30°.
建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
解:在等腰Rt△BCD中,∠ACD=90°,
∴AB=AC-BC=55.2-40=15.2 (m).
∴AC=DC·tan∠ADC
=tan54°×40≈1.38×40=55.2(m).
解:由题意,AC=AB=610(米).
目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(tan39°≈0.81) (1) 求大楼与电视塔之间的距离AC;
解:DE=AC=610(米), 在Rt△BDE中, .
(2) 求大楼的高度CD(精确到1米).
∴ BE=DEtan39°. ∵CD=AE,∴CD=AB-DE·tan39° =610-610×tan39° ≈116(米).
利用仰角和俯角解直角三角形
运用解直角三角形解决仰角、俯角问题
初中数学人教版九年级下册28.2 解直角三角形及其应用图文课件ppt: 这是一份初中数学人教版九年级下册28.2 解直角三角形及其应用图文课件ppt,共19页。PPT课件主要包含了温故知新,引入新课,教学活动,课堂小结,课堂小结与作业布置,作业布置等内容,欢迎下载使用。
数学九年级下册第二十八章 锐角三角函数综合与测试课前预习ppt课件: 这是一份数学九年级下册第二十八章 锐角三角函数综合与测试课前预习ppt课件,共18页。PPT课件主要包含了解答下面的问题,=80×cos25°,≈72505海里,跟踪训练,在Rt△ABF中,解得x6,i213,i1115等内容,欢迎下载使用。
初中数学人教版九年级下册28.2 解直角三角形及其应用图文ppt课件: 这是一份初中数学人教版九年级下册28.2 解直角三角形及其应用图文ppt课件,共27页。PPT课件主要包含了学习目标,新课导入,知识点1,知识讲解,即学即练,知识点2,随堂练习,拓展练习等内容,欢迎下载使用。













