初中数学17.1 勾股定理优秀课件ppt

这是一份初中数学17.1 勾股定理优秀课件ppt，共29页。PPT课件主要包含了素养目标，勾股定理的认识与证明，SA+SBSC，结论仍然成立，拼图证明，赵爽拼图证明法，拼过程展示，“赵爽弦图”，∵S大正方形＝c2，勾股定理等内容，欢迎下载使用。

数学家曾建议用这个图作为与“外星人”联系的信号.
1. 了解勾股定理的发现过程，掌握勾股定理的内容，会用面积法证明勾股定理.
2. 能用勾股定理解决一些简单问题.
3. 通过用多种方法证明勾股定理，培养学生发散思维能力.
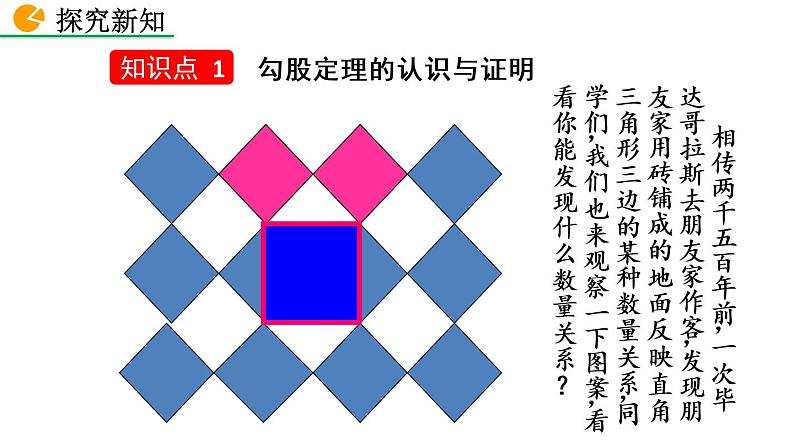
相传两千五百年前，一次毕达哥拉斯去朋友家作客，发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系，同学们，我们也来观察一下图案，看看你能发现什么数量关系？
2.由这三个正方形A，B，C的边长构成的等腰直角三角形三条边长度之间有怎样的特殊关系？
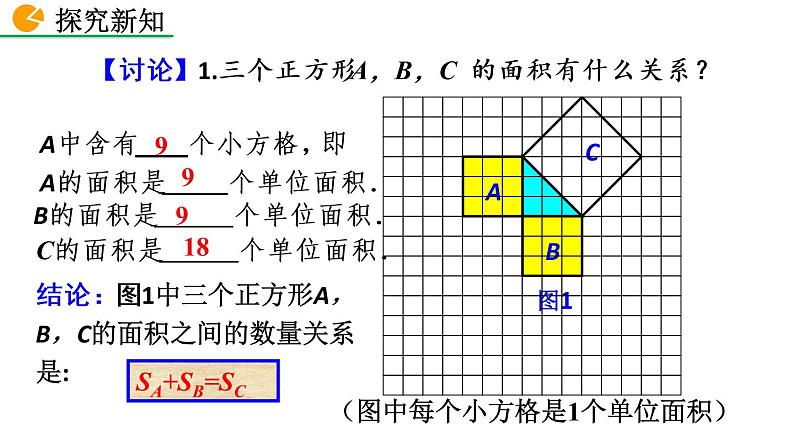
　　 【思考】1.三个正方形A，B，C 的面积有什么关系？　　
（图中每个小方格是1个单位面积）
A中含有____个小方格，即A的面积是 个单位面积．
B的面积是 个单位面积．
C的面积是 个单位面积．
结论：图1中三个正方形A，B，C的面积之间的数量关系是:
　　【讨论】1.三个正方形A，B，C 的面积有什么关系？　　
【讨论】2. SA+SB=SC在图2中还成立吗？
A的面积是 个单位面积．
B的面积是 个单位面积．
C的面积是 个单位面积．
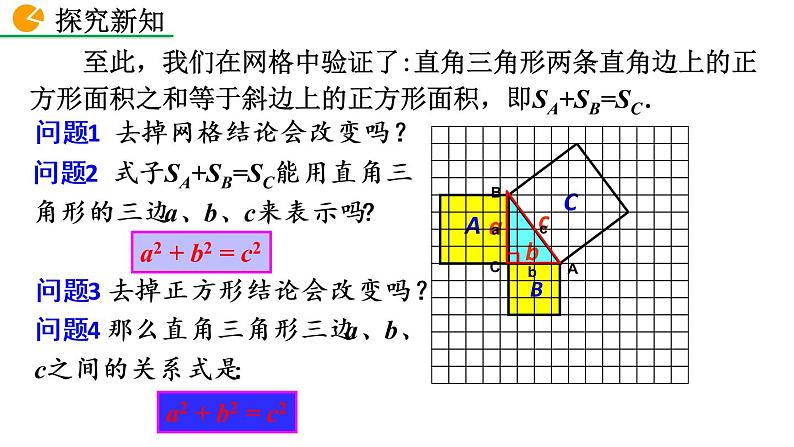
问题2 式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗?
问题4 那么直角三角形三边a、b、c之间的关系式是:
至此，我们在网格中验证了:直角三角形两条直角边上的正方形面积之和等于斜边上的正方形面积，即SA+SB=SC .
a2 + b2 = c2
问题1 去掉网格结论会改变吗？
问题3 去掉正方形结论会改变吗？
命题1：如果直角三角形的两直角边长分别为a，b,斜边长为c，那么a2+b2=c2.
是不是所有的直角三角形都具有这样的结论呢？光靠实验和猜想还不能把问题彻底搞清楚. 这就需要我们对一般的直角三角形进行证明．下面我们就一起来探究，看一看我国古代数学家赵爽是怎样证明这个命题的．
以直角三角形的两条直角边a、b为边作两个正方形，把两个正方形如图1连在一起，通过剪、拼把它拼成图2的样子.你能做到吗？试试看.
小组活动：仿照课本中赵爽的思路，只剪两刀，将两个连体正方形，拼成一个新的正方形.
S小正方形＝(b-a)2,
∴S大正方形＝4·S三角形＋S小正方形，
毕达哥拉斯证法：请先用手中的四个全等的直角三角形按图示进行拼图，然后分析其面积关系后证明吧.
∴a2+b2+2ab=c2+2ab，
∴a2 +b2 =c2.
证明：∵S大正方形=(a+b)2=a2+b2+2ab,
∴a2 + b2 = c2.
美国第二十任总统伽菲尔德的“总统证法”.
如图，图中的三个三角形都是直角三角形，求证：a2 + b2 = c2.
如果直角三角形两直角边分别为a、b,斜边为c，那么
即直角三角形两直角边的平方和等于斜边的平方.
表示为：Rt△ABC中，∠C=90°,
　　勾股定理给出了直角三角形三边之间的关系，即两直角边的平方和等于斜边的平方.
a2 + b2 =c2
求下列图中字母所表示的正方形的面积.
例1 如图，在Rt△ABC中， ∠C=90°.
（1）若a=b=5,求c;
（2）若a=1,c=2,求b.
利用勾股定理求直角三角形的边长
设直角三角形的两条直角边长分别为a和b，斜边长为c.（1）已知a=6，c=10，求b；（2）已知a=5，b=12，求c； （3）已知c=25，b=15，求a.
解：由勾股定理得52+122=c2 , c=13;
解：由勾股定理得62+b2=102, b=8;
解：由勾股定理得a2+152=252 , a=20.
（1）若a：b=1：2 ，c=5,求a;
（2）若b=15，∠A=30°,求a,c.
例2 在Rt△ABC中， ∠C=90°.
x2+(2x)2=52，
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152，
提示：已知直角三角形两边关系和第三边的长求未知两边时，要运用方程思想设未知数，根据勾股定理列方程求解.
勾股定理和方程相结合求直角三角形的边长
求出下列直角三角形中未知边的长度：
解：（1）由勾股定理得：
∵ x2+52=132
∴ x2=132-52
1.在直角三角形中，若勾为3，股为4，则弦为（　　）A．5 B．6 C．7 D．8
1. 若一个直角三角形的两直角边长分别为9和12，则斜边的长为（ ） A.13 B.17 C. 15 D.18
2.若一个直角三角形的斜边长为17，一条直角边长为15，则另一直角边长为（ ） A.8 B.40 C.50 D.36
3.在Rt△ABC中，∠C=90°，若a︰b=3︰4，c=100，则a= _____，b = ______.
4．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm,则正方形A，B，C，D的面积之和为___________cm2 ．
在Rt△ABC中，AB＝4，AC＝3，求BC的长.
解：本题斜边不确定，需分类讨论：当AB为斜边时，如图，当BC为斜边时，如图，
提示：当直角三角形中所给的两条边没有指明是斜边或直角边时，其中一较长边可能是直角边，也可能是斜边，这种情况下一定要进行分类讨论，否则容易丢解.
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解：由勾股定理可得 AB2=AC2+BC2=25，即 AB=5. 根据三角形面积公式， ∴ AC×BC= AB×CD. ∴ CD= .
提示：由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积，它常与勾股定理联合使用．
在Rt△ABC中， ∠C=90°,a,b为直角边，c为斜边，则有a2+b2=c2.
已知两边没有指明是直角边还是斜边时一定要分类讨论