
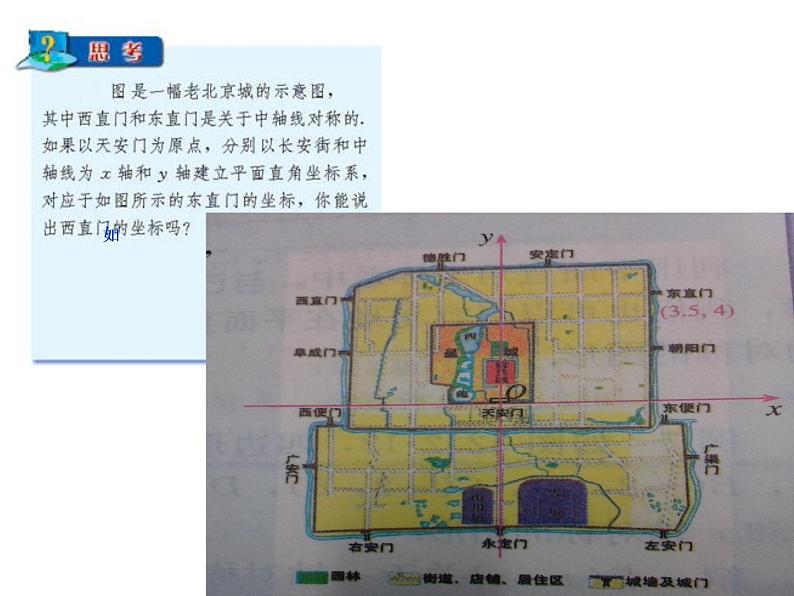


人教版八年级上册13.2 画轴对称图形综合与测试教案配套ppt课件
展开1.探索利用坐标来表示轴对称.2.掌握关于x轴、y轴对称的点的坐标特点.
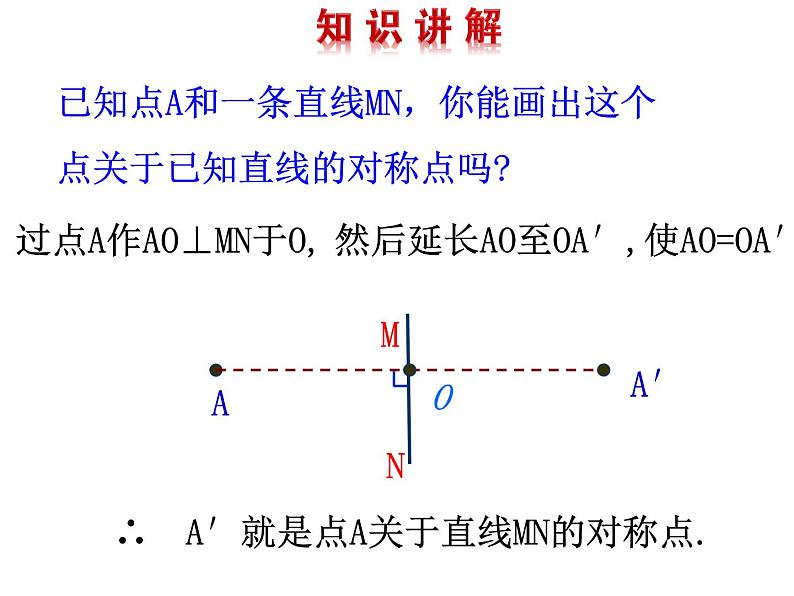
已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗?
∴ A′就是点A关于直线MN的对称点.
然后延长AO至OA′,使AO=OA′.
过点A作AO⊥MN于O,
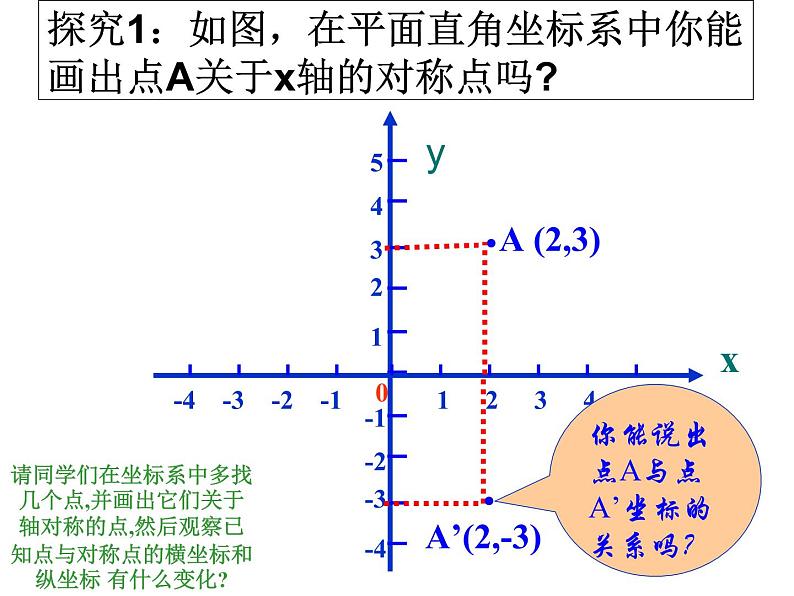
探究1:如图,在平面直角坐标系中你能画出点A关于x轴的对称点吗?
你能说出点A与点A’坐标的关系吗?
请同学们在坐标系中多找几个点,并画出它们关于轴对称的点,然后观察已知点与对称点的横坐标和纵坐标 有什么变化?
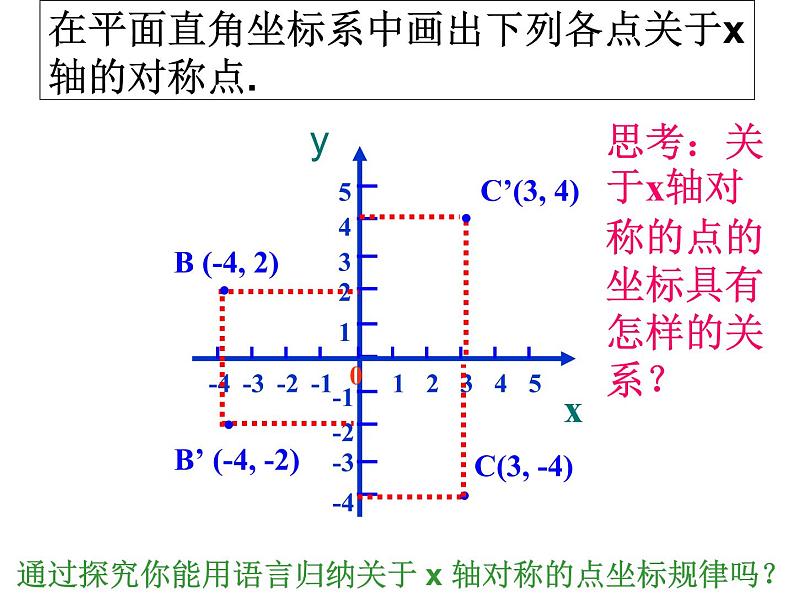
在平面直角坐标系中画出下列各点关于x轴的对称点.
B’ (-4, -2)
思考:关于x轴对称的点的坐标具有怎样的关系?
通过探究你能用语言归纳关于 x 轴对称的点坐标规律吗?
归纳:关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
练习:1、点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为________.2、点M (a, -5)与点N(-2, b)关于x轴对称,则a=___, b =____.
(- 5 , -6 )
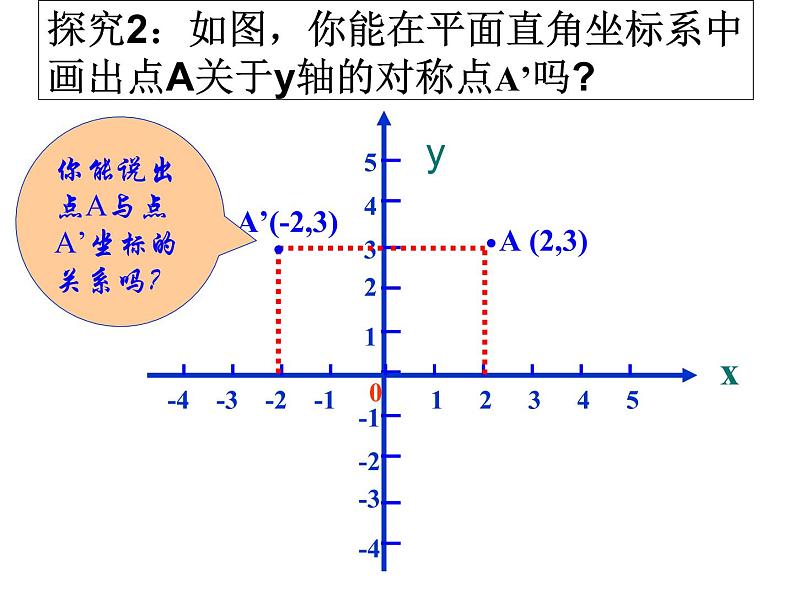
探究2:如图,你能在平面直角坐标系中画出点A关于y轴的对称点A’吗?
在平面直角坐标系中画出下列各点关于y轴的对称点.
思考:关于y轴对称的点的坐标具有怎样的关系?
归纳:关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
练习:1、点P(-5, 6)与点Q关于y轴对称,则点Q的坐标为________.2、点M (a, -5)与点N(-2, b)关于y轴对称,则a=___, b =____.
小结:在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
点(x, y)关于x轴对称的点的坐标为 ______.点(x, y)关于y轴对称的点的坐标为 ______.
已知点关于x轴或y轴对称的点的坐标变化规律: ( P44)
在平面直角坐标系中,画出下列已知点及其关于x 轴对称的点,把它们的坐标填入表格中.
探究并归纳已知点关于坐标轴对称的点的坐标变化规律 (教材P69)
探究并归纳已知点关于坐标轴对称的点的坐标变化规律
关于x 轴对称的每对对称点的横坐标相等,纵坐标互为相反数.
观察下图中关于x 轴对称的每对对称点的坐标有怎 样的变化规律?
在平面直角坐标系中,画出下列已知点及其关于y 轴对称的点,把它们的坐标填入表格中.
观察关于y 轴对称的每对对称点的坐标有怎样的变化规律?
关于y 轴对称的每对对称点的横坐标互为相反数,纵坐标相等.
点(x,y)关于x 轴对称的点的坐标为(___,____); 点(x,y)关于y 轴对称的点的坐标为(___,____).
x -y
- x y
横轴横相等,纵轴纵相等。
【解析】点A(-3,5),B(-4,1),C(-1,3),关于y轴对称点的坐标分别为A′(3,5),B′(4,1),C′(1,3).依次连接A′B′,B′C′,C′A′,就得到△ABC关于y轴对称的图形,即△A′B′C′.
已知△ABC的三个顶点的坐标分别为A(-3,5),B(-4,1) , C(-1,3),作出△ABC关于y轴对称的图形.
先求出已知图形中一些特殊点(多边形的顶点)的对称点的坐标,描出并连接这些点,就可以得到这个图 形的轴对称图形. 步骤简述为:(1)求特殊点的坐标;(2)描点;(3)连线.
归纳画一个图形关于x 轴或y 轴对称的图形的方法和步骤.
例 如图,四边形ABCD 的四个顶点的坐标分别为 A(-5,1),B(-2,1),C(-2,5),D(-5,4), 分别画出与四边形ABCD 关于x 轴和y 轴对称的图形.
解:点(x,y)关于y 轴对称的点的坐标为(-x,y),因此四边形ABCD 的顶点A,B,C,D 关于y 轴对称的点分别为: A′( , ), B′( , ), C′( , ), D′( , ),
2 5
5 1
2 1
5 4
解:依次连接 , , , ,就可得到与四边形ABCD 关于y轴对称的四边形 .
请在图上画出四边形ABCD 关于x 轴对称的图形.
A’’(-5,-1)B’’(-2,-1)C’’(-2,-5)D’’(-5,-4)
练习:P71的 T2,3
练习1 分别写出下列各点关于x 轴和y 轴对称的点的坐标:(-2,6),(1,-2), (-1,3) ,(-4,-2),(1,0)
解:关于x 轴对称的点的坐标:(-2,-6),(1,2),(-1,-3),(-4,2),(1,0) 关于y 轴对称的点的坐标:(2,6),(-1,-2), (1,3),(4,-2),(-1,0) .
练习:P70的 T1
(拓展提高) 思考:如图,分别作出点P,M,N关于直线x=1的对称点, 你能发现它们坐标之间分别有什么关系吗?
类似: 若两点(x1,y1)、(x2,y2)关于 直线y=n对称,则 ,n=
归纳: 若两点(x1,y1)、(x2,y2)关于直线x=m对称,则m= , .
练习2 若点P(2a+b,-3a)与点 P′(8,b+2)关于x 轴对称,则a = ,b= ;若关于y 轴对称,则a = ,b=______.
【P71,T2】分别写出下列各点关于x 轴和y 轴对称的点的坐标. (3,6)、(-7,9)、(6,-1)、(0,10)
解:关于y轴对称的点的坐标: (-3,6),(7, 9),(-6,-1),(0,10) 关于x 轴对称的点的坐标: (3,-6),(-7,-9),(6,1),(0,-10)
以正方形ABCD 的中心为原点建立平面直角坐标系.点A 的坐标为(1,1)、写出点B,C,D 的坐标.
成功:A=x+y+z.A代表成功,x代表艰苦的劳动,y代表正确的方法,Z代表少说空话. ——爱因斯坦
课本71页 第2题、课本72页 第5题.
初中数学人教版八年级上册第十三章 轴对称13.2 画轴对称图形13.2.1 作轴对称图形教学ppt课件: 这是一份初中数学人教版八年级上册第十三章 轴对称13.2 画轴对称图形13.2.1 作轴对称图形教学ppt课件,共30页。PPT课件主要包含了学习目标,新课导入,复习引入,新知探究,成轴对称,跟踪训练,动手试一试吧,课堂小结,画轴对称图形,注意事项等内容,欢迎下载使用。
2020-2021学年13.2 画轴对称图形综合与测试图文课件ppt: 这是一份2020-2021学年13.2 画轴对称图形综合与测试图文课件ppt,共33页。PPT课件主要包含了简称横轴横相等,课堂小结等内容,欢迎下载使用。
数学人教版13.2 画轴对称图形综合与测试教学课件ppt: 这是一份数学人教版13.2 画轴对称图形综合与测试教学课件ppt,共33页。PPT课件主要包含了复习回顾,动手操作,甲同学,乙同学,丙同学,规范作图,归纳新知,BED,若可以该怎么剪,课堂小结等内容,欢迎下载使用。













