初中数学12.3 角的平分线的性质课文内容课件ppt

这是一份初中数学12.3 角的平分线的性质课文内容课件ppt，共16页。PPT课件主要包含了角平分线的性质，∴PD＝PE，用符号语言表述，温故知新，想一想，用符号语言表示为，说一说，学习例题，走进生活，用数学语言表示为等内容，欢迎下载使用。

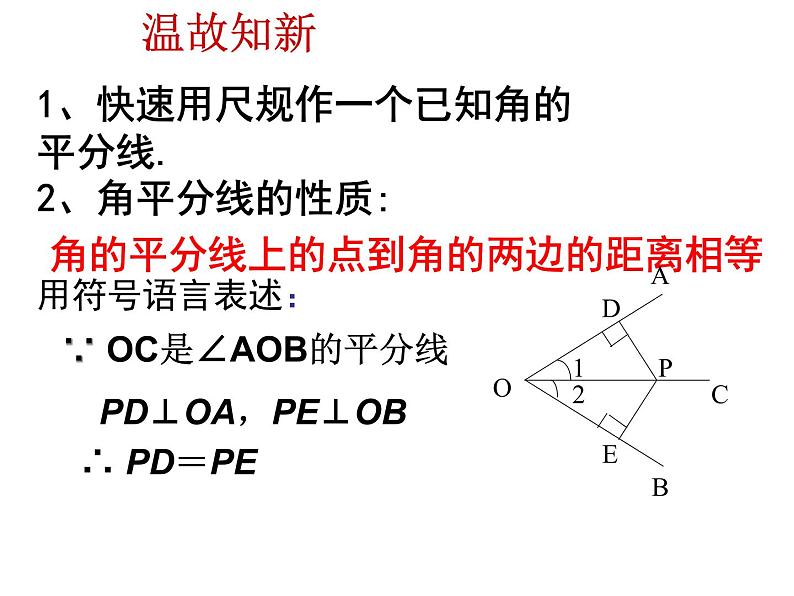
1、快速用尺规作一个已知角的平分线.
角的平分线上的点到角的两边的距离相等
PD⊥OA，PE⊥OB
∵ OC是∠AOB的平分线
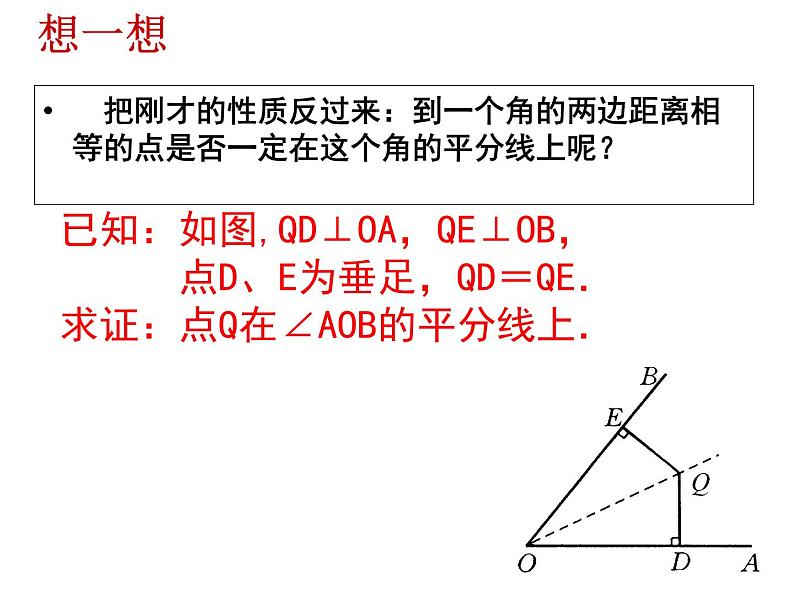
把刚才的性质反过来：到一个角的两边距离相等的点是否一定在这个角的平分线上呢？
已知：如图,QD⊥OA，QE⊥OB， 点D、E为垂足，QD＝QE．求证：点Q在∠AOB的平分线上．
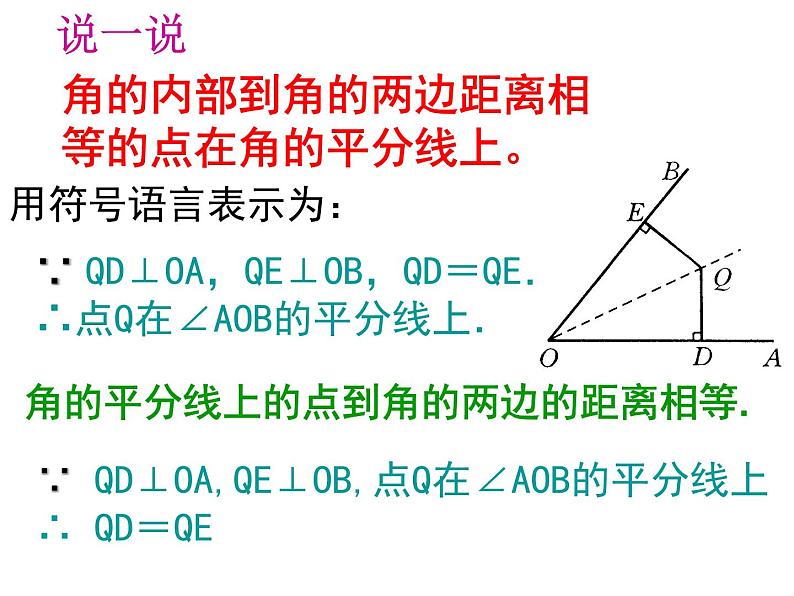
角的内部到角的两边距离相等的点在角的平分线上。
∵ QD⊥OA，QE⊥OB，QD＝QE．∴点Q在∠AOB的平分线上．
角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上∴ QD＝QE
所以： 角平分线可以看做到角的两边距离相等的所有点的集合
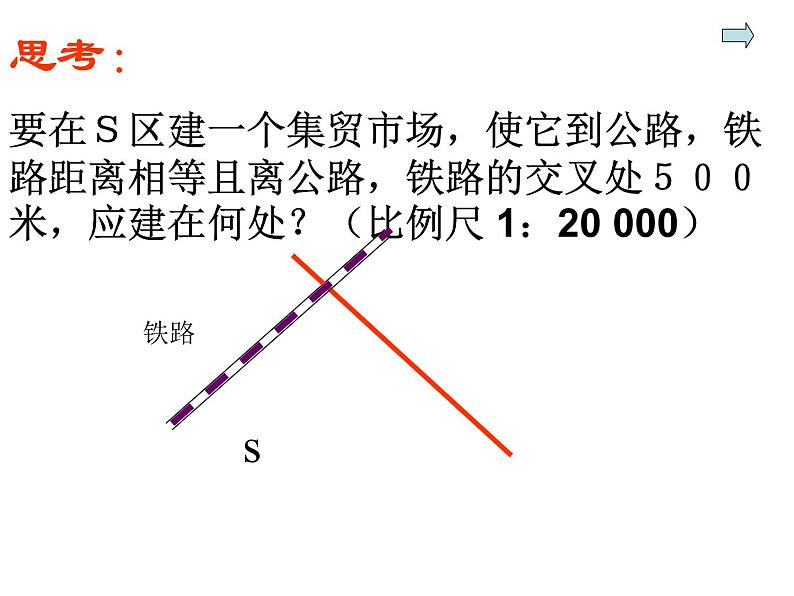
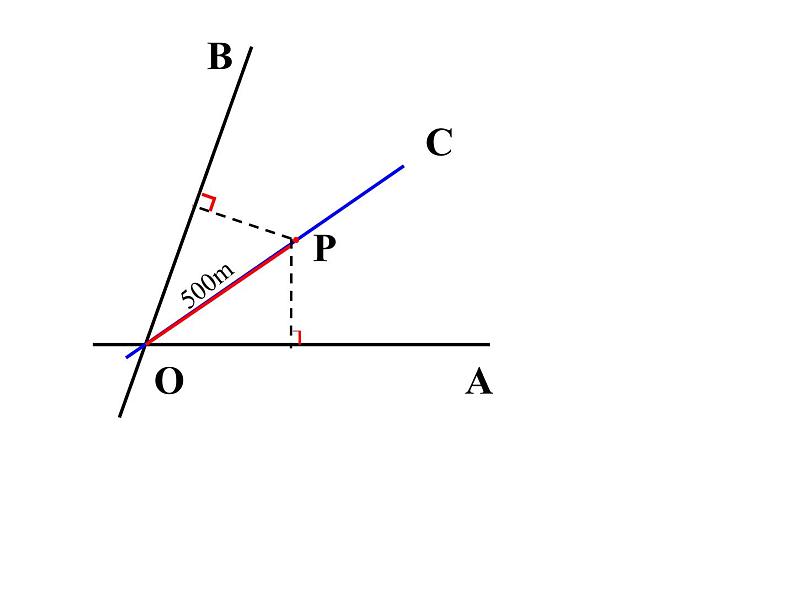
思考：要在Ｓ区建一个集贸市场，使它到公路，铁路距离相等且离公路，铁路的交叉处５００米，应建在何处？（比例尺 1：20 000）
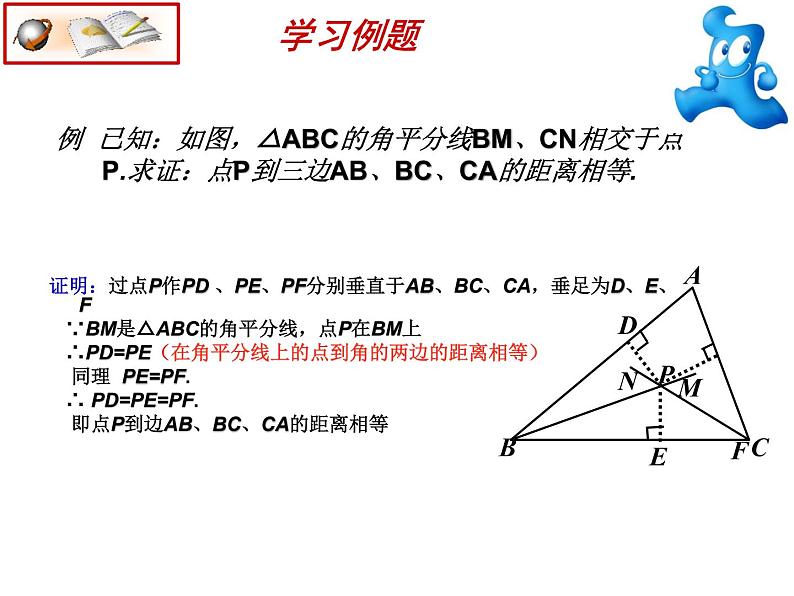
例 已知：如图，△ABC的角平分线BM、CN相交于点P.求证：点P到三边AB、BC、CA的距离相等.
证明：过点P作PD 、PE、PF分别垂直于AB、BC、CA，垂足为D、E、F ∵BM是△ABC的角平分线，点P在BM上 ∴PD=PE（在角平分线上的点到角的两边的距离相等） 同理 PE=PF. ∴ PD=PE=PF. 即点P到边AB、BC、CA的距离相等
1、如图，为了促进当地旅游发展，某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
在确定度假村的位置时,一定要画出三个角的平分线吗?你是怎样思考的?你是如何证明的?
2、直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:( ) A.一处 B. 两处 C.三处 D.四处
分析:由于没有限制在何处选址,故要求的地址共有四处。
将你今天的收获与大家共同分享吧！
到角的两边的距离相等的点在角的平分线上。
角平分线可以看做到角的两边距离相等的 所有点的集合
2、如图，已知△ABC的外角∠CBD和∠BCE的平分线相交于点F，求证：点F在∠DAE的平分线上．
3、如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F，且BE＝CF。 求证：AD是△ABC的角平分线。