数学24.1.2 垂直于弦的直径说课课件ppt

这是一份数学24.1.2 垂直于弦的直径说课课件ppt，共28页。PPT课件主要包含了知识回顾，随堂训练1填空，挖掘潜力等内容，欢迎下载使用。

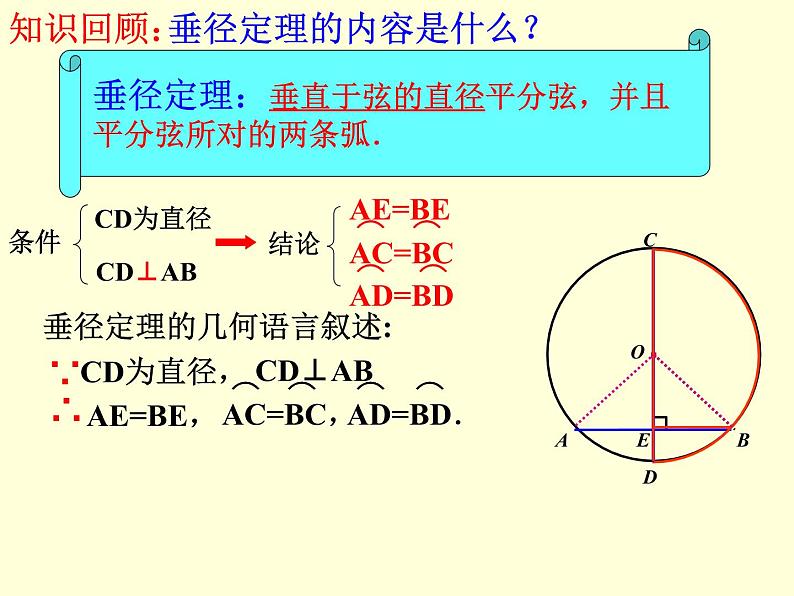
垂径定理的几何语言叙述:
垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧．
垂径定理的内容是什么？
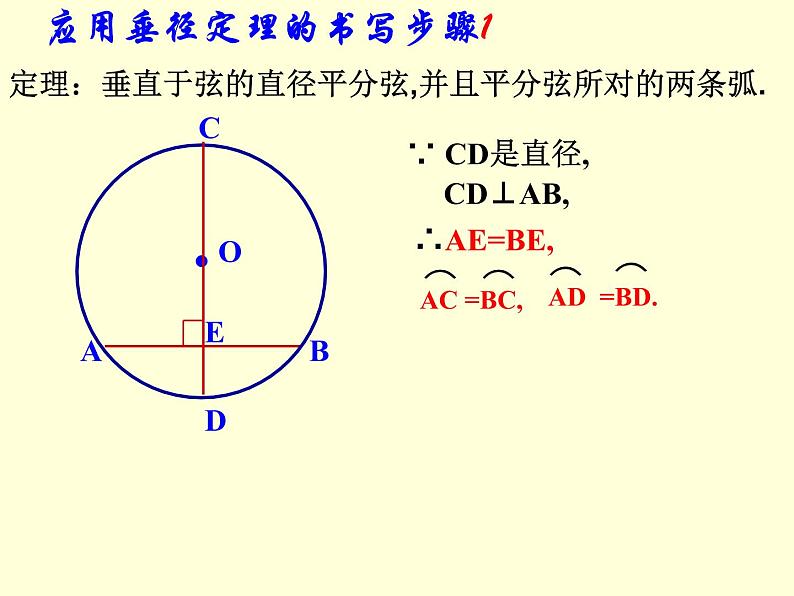
应用垂径定理的书写步骤1
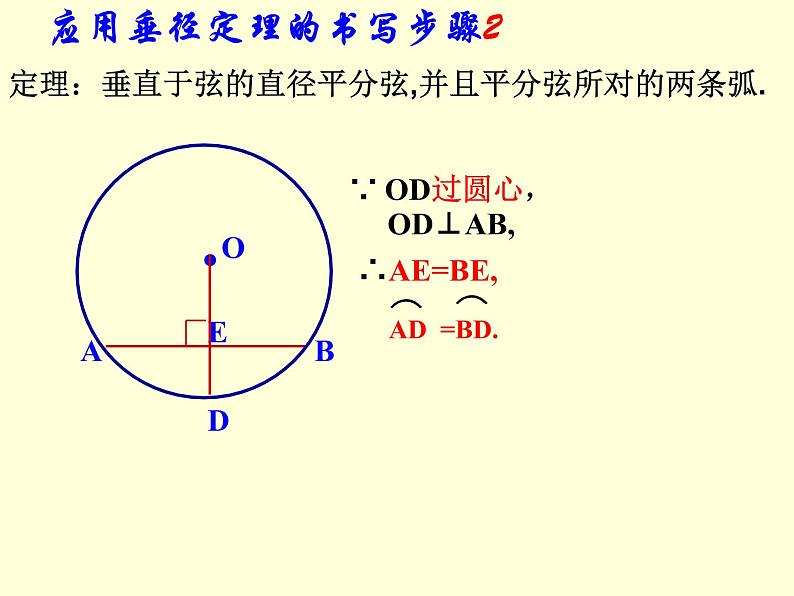
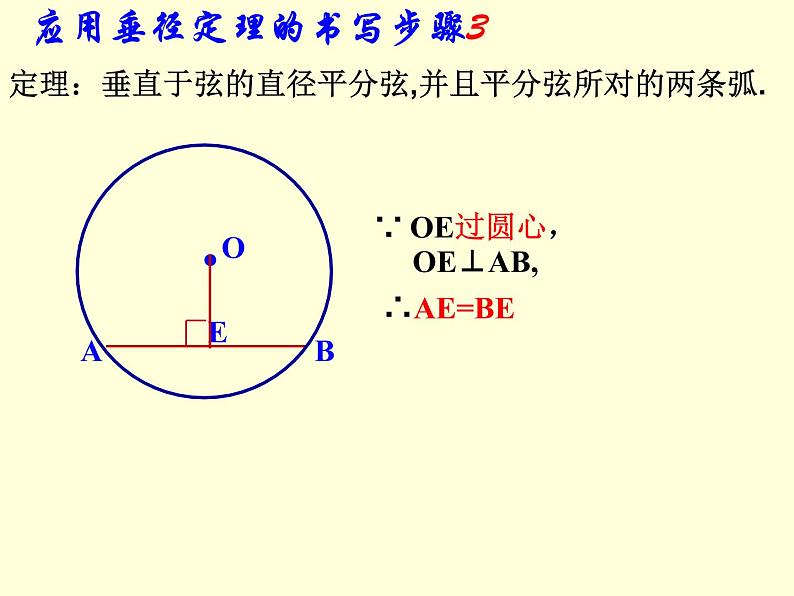
定理：垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵ CD是直径,
应用垂径定理的书写步骤2
应用垂径定理的书写步骤3
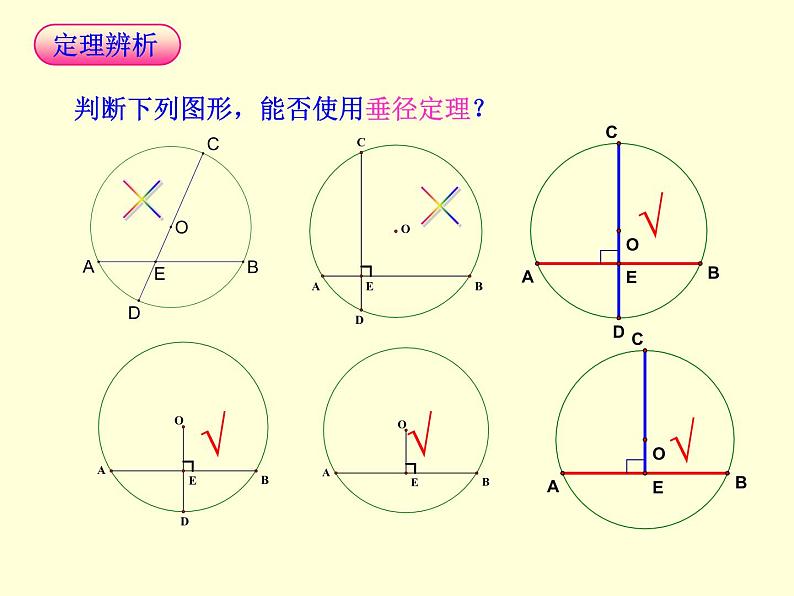
判断下列图形，能否使用垂径定理？
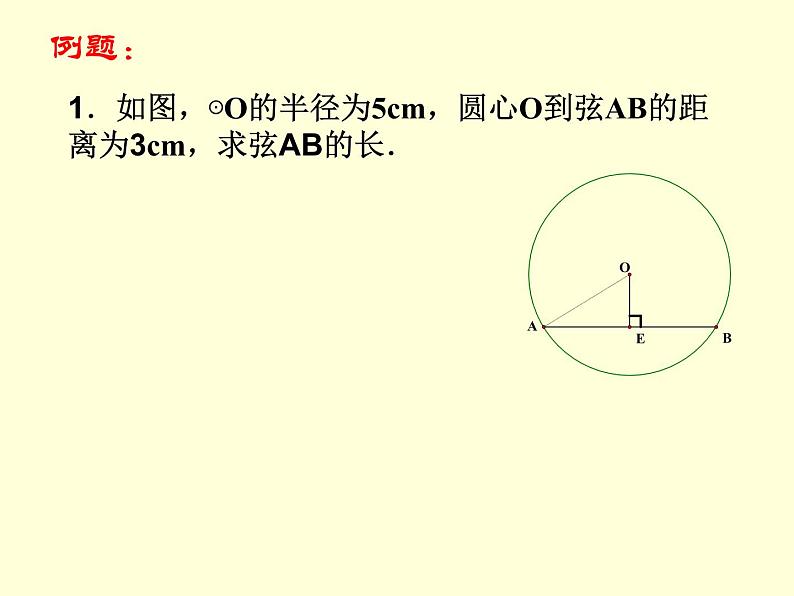
1．如图，⊙O的半径为5cm，圆心O到弦AB的距离为3cm，求弦AB的长．
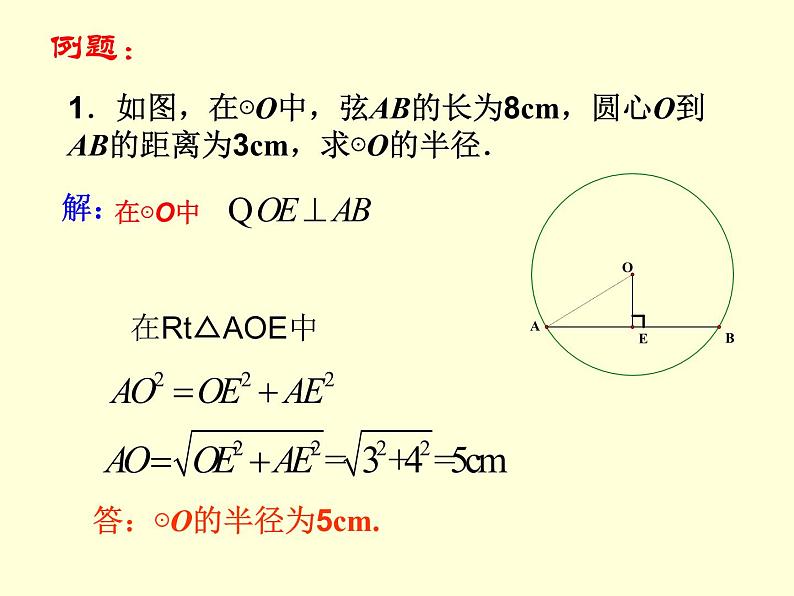
1．如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径．
答：⊙O的半径为5cm.
1.如图，⊙O 中，弦AB 的长为8 cm ，弓形ADB的高为2 cm ，求⊙O 半径.
答：⊙O 的半径为5 cm.
2、如图4，在⊙O中，AB为⊙O的弦，C、D是直线AB上两点，且0C＝OD.求证：AC=BD
3、如图4，在⊙O中，AB为⊙O的弦，C、D是直线AB上两点，且AC＝BD求证：△OCD为等腰三角形。
4、如图，两个圆都以点O为圆心，小圆的弦CD与大圆的弦AB在同一条直线上。你认为AC与BD的大小有什么关系？为什么？
5. 已知⊙O 的半径为5，⊙O 的两条平行弦AB＝6，CD＝8，那么AB 与CD 间的距离等于多少？
解: （1）若AB、CD 在圆心的同侧，过O 作 OF ⊥ AB 交CD 于E ∵AB∥CD
∴CD⊥OE ，连结OA、OC∴AF=BF=3 CE=EB=4
∴OE= ∴EF=4-3=1
（2）若AB、CD 在圆心O 的两侧
同上，可求得OF＝4、OE＝3
∴AB与CD 间的距离EF＝4+3＝7
6.如图，P为⊙O的弦BA延长线上一点，PA＝AB＝2，PO＝5，求⊙O的半径。
关于弦的问题，常常需要过圆心作弦的垂线段，这是一条非常重要的辅助线。圆心到弦的距离、半径、弦长构成直角三角形，便将问题转化为直角三角形的问题。
7．如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ADOE是正方形．
∴四边形ADOE为矩形，
∴ 四边形ADOE为正方形.
8.已知：在⊙O中，弦AB⊥CD于P，⊙O的半径为5，AB=8，CD=6，OE⊥AB，OF⊥CD。求四边形OEPF的周长
(1)已知AB、CD是⊙O中互相垂直的弦，并且AB把CD分成3cm和7cm的两部分，则弦和圆心的距离为——cm.(2)已知⊙O的半径为10cm，弦MN∥EF,且MN=12cm,EF=16cm,则弦MN和EF之间的距离为——.(3)已知⊙O中，弦AB=8cm，圆心到AB的距离为3cm，则此圆的半径为——(4)在半径为25cm的⊙O中，弦AB=40cm，则此弦和弦所对的弧的中点的距离是——(5) ⊙O的直径AB=20cm, ∠BAC=30°则弦AC=——(6)P为⊙O内一点，OP=3cm，⊙O半径为5cm，则经过P点的最短弦长为________；最长弦长为_______．
2、已知：如图，⊙O 中， AB为 弦，C 为 弧AB 的中点，OC交AB 于D ，AB = 6cm ，CD = 1cm. 求⊙O 的半径OA.
3、如图为一圆弧形拱桥，半径OA = 10m，　　拱高为4m，求拱桥跨度AB的长。
4．如图，AB为⊙O直径，E是弧BC中点，OE交BC于点D，BD=3，AB=10，则AC=_____
某地有一座圆弧形拱桥圆心为Ｏ，桥下水面宽度为７、2 m ，过O 作OC ⊥ AB 于D， 交圆弧于C，CD=2、4m， 现有一艘宽3m，船舱顶部为方形并高出水面（AB）2m的货船要经过拱桥，此货船能否顺利通过这座拱桥？
解决有关弦的问题，经常是过圆心作弦的垂线，连结半径等辅助线，为应用垂径定理创造条件。