


人教B版 (2019)必修 第四册11.3.1 平行直线与异面直线精品课件ppt
展开如图所示,直线 AB、CD被直线EF所截,形成了8个角.
(1)同位角:两个角都在两条直线的同侧,并且在第三条直线(截线)的同旁,这样的一对角叫做同位角.如∠1和∠5,∠3和∠7,∠4和∠8,∠2和∠6. (2)内错角:两个角都在两条直线之间,并且在第三条直线(截线)的两旁,这样的一对角叫做内错角.例如∠3和∠5,∠4和∠6. (3)同旁内角:两个角都在两条直线之间,并且在第三条直线(截线)的同旁,这样的一对角叫做同旁内角.例如∠4和∠5,∠3和∠6.
两条直线被第三条直线所截,如果 (1)同位角相等,两直线平行. (2)内错角相等,两直线平行. (3)同旁内角互补,两直线平行.
(4)经过直线外一点,有且只有一条直线与这条直线平行
(5)如果两条直线都和第三条直线平行,这两条直线也互相平行
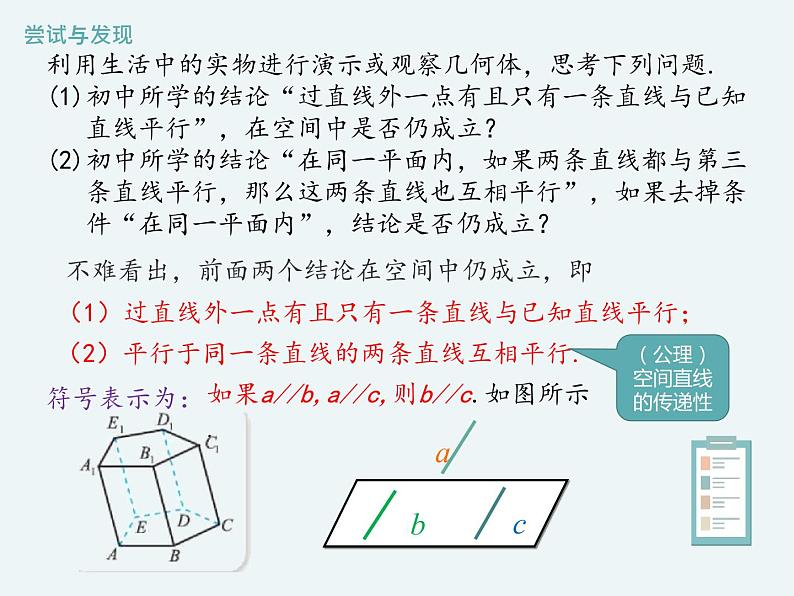
利用生活中的实物进行演示或观察几何体,思考下列问题.(1)初中所学的结论“过直线外一点有且只有一条直线与已知 直线平行”,在空间中是否仍成立?(2)初中所学的结论“在同一平面内,如果两条直线都与第三 条直线平行,那么这两条直线也互相平行”,如果去掉条 件“在同一平面内”,结论是否仍成立?
不难看出,前面两个结论在空间中仍成立,即
(1)过直线外一点有且只有一条直线与已知直线平行;
(2)平行于同一条直线的两条直线互相平行.
如果a//b,a//c,则b//c.如图所示.
(公理)空间直线的传递性
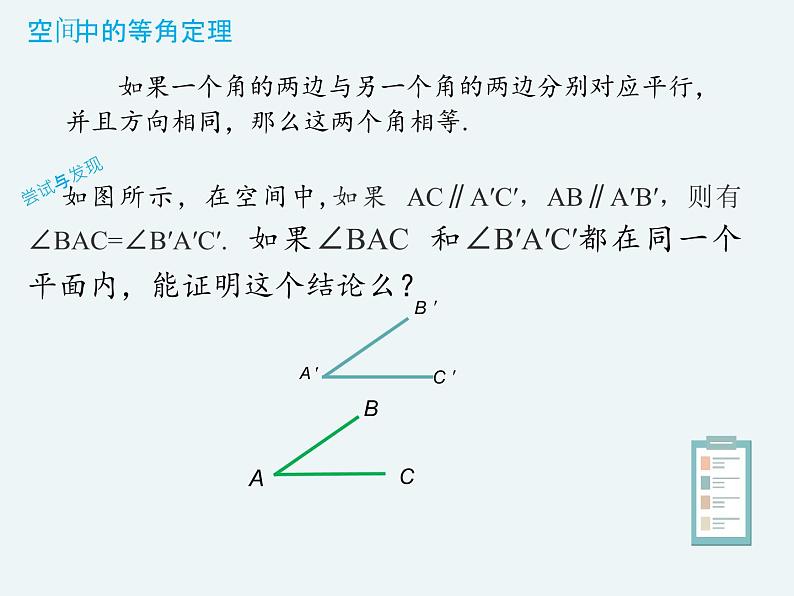
如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等.
如图所示,在空间中,如果 AC∥A′C′,AB∥A′B′,则有∠BAC=∠B′A′C′. 如果∠BAC 和∠B′A′C′都在同一个平面内,能证明这个结论么?
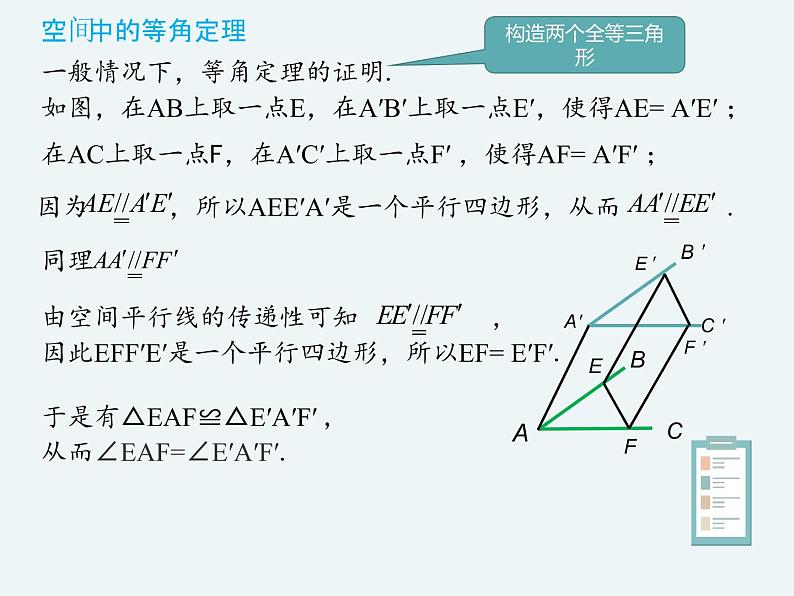
一般情况下,等角定理的证明.
如图,在AB上取一点E,在A′B′上取一点E′,使得AE= A′E′ ;
在AC上取一点F,在A′C′上取一点F′ ,使得AF= A′F′ ;
于是有△EAF≌△E′A′F′ ,从而∠EAF=∠E′A′F′.
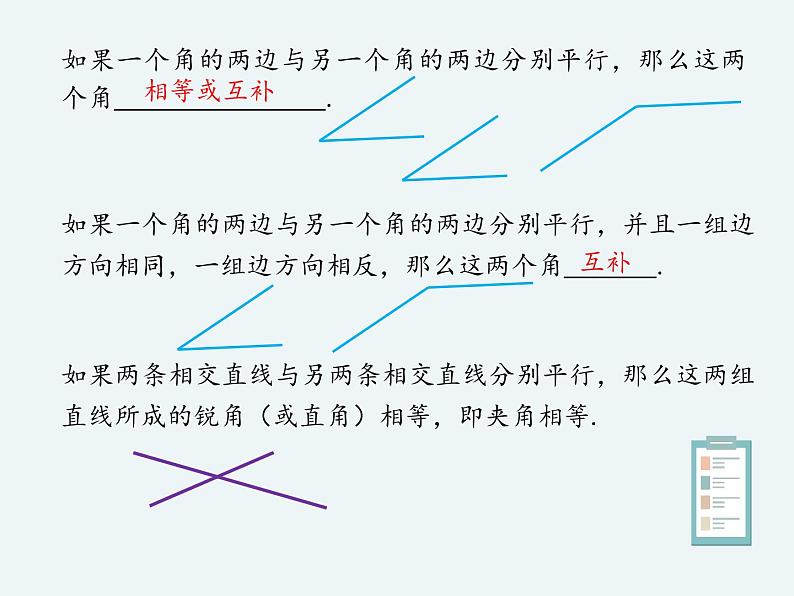
如果一个角的两边与另一个角的两边分别平行,那么这两个角 .
如果一个角的两边与另一个角的两边分别平行,并且一组边方向相同,一组边方向相反,那么这两个角 .
如果两条相交直线与另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等,即夹角相等.
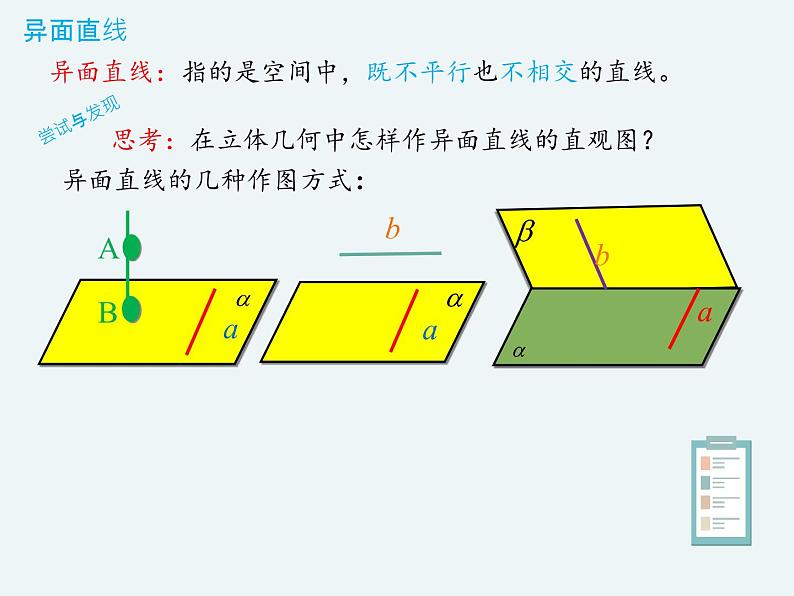
指的是空间中,既不平行也不相交的直线。
思考:在立体几何中怎样作异面直线的直观图?
异面直线的几种作图方式:
异面直线的一种判定方法:与一个平面相交于一点的直线与这个平面内不经过交点的直线异面.
判定定理:与一个平面相交于一点的直线与这个平面内 不经过交点的直线异面.
定义法:异面直线是空间中,既不平行也不相交的直线。
两条异面直线所成角:直线a,b是异面直线,经过空间任意一点O,分别引直线a' ‖ a,b' ‖ b.直线a'和b'所成的锐角(或直角)叫作异面直线a和b所成的角.
两异面直线的距离:和两条异面直线都垂直相交的直 线叫作两条异面直线的公垂线. 两条异面直线的公垂线在这两条 异面直线间的线段的长度,叫作 两条异面直线的距离.
空间四边形:顺次连接不共面的4点所构成的图形.
其中4个点都是空间四边形的顶点,连接相邻顶点间的线段称为空间四边形的边,连接不相邻顶点间的线段称为空间四边形的对角线.
如图所示空间四边形ABCD中,E,F,G,H分别是边AB,AD,CB,CD的中点.求证:四边形EFHG平行四边形.
(思考)EFHG是菱形时,空间四边形ABCD分别满足什么条件?
(思考)EFHG是矩形时,空间四边形ABCD分别满足什么条件?
画两个相交平面,在这两个平面内各画一条直线,使这两条直线分别成为
❸判断下列命题的真假.(1) 4条边相等的空间四边形是菱形; (2) 空间中,与同一条直线异面的两条直线一定异面; (3) 空间中,如果∠BAC=∠B'A'C'且则 AC//A'C'.
(1)两对连接两邻边中点的线段互相平行且相等,且都 等于与之平行的对角线的一半.
(2)由于每三条依次相邻的边的中点都不在同一直线上, 是三角形的顶点.
(3)若两对角线互相垂直,则四边形中点连线所成的平 行四边形为矩形.
(4)若空间四边形中,对边中点的连线垂直且平分对边, 则称其为等腰偏斜梯形,且这对对边中点的连线称 为等腰偏斜梯形的对称轴.
1.平行直线的传递性平行于同一条直线的两条直线互相平行.符号表示:如果a∥b,a∥c,则b∥c.
2.等角定理如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等.
3.异面直线:不能同时在任何一个平面内的两条直线.判定方法:与一个平面相交于一点的直线与这个平面内不经过交点的直线异面.
人教B版 (2019)必修 第四册第十一章 立体几何初步11.3 空间中的平行关系11.3.1 平行直线与异面直线多媒体教学课件ppt: 这是一份人教B版 (2019)必修 第四册第十一章 立体几何初步11.3 空间中的平行关系11.3.1 平行直线与异面直线多媒体教学课件ppt,文件包含人教B版高中数学必修第四册第11章1131平行直线与异面直线课件ppt、人教B版高中数学必修第四册第11章1131平行直线与异面直线学案doc、人教B版高中数学必修第四册课后素养落实16平行直线与异面直线含答案doc等3份课件配套教学资源,其中PPT共49页, 欢迎下载使用。
高中数学人教B版 (2019)必修 第四册11.3.1 平行直线与异面直线图片ppt课件: 这是一份高中数学人教B版 (2019)必修 第四册11.3.1 平行直线与异面直线图片ppt课件,共46页。PPT课件主要包含了有且只有一条,互相平行,传递性,b∥c,对应平行,直线与直线平行的证明,等角定理及其应用等内容,欢迎下载使用。
高中数学人教B版 (2019)必修 第四册11.3.1 平行直线与异面直线教课内容ppt课件: 这是一份高中数学人教B版 (2019)必修 第四册11.3.1 平行直线与异面直线教课内容ppt课件,共20页。PPT课件主要包含了问题1平行直线,3图形表述,知识点2等角定理,问题2异面直线,知识点异面直线,问题3空间四边形等内容,欢迎下载使用。













