
【数学】贵州省遵义航天高级中学2019-2020学年高二上学期第一次月考试题
展开
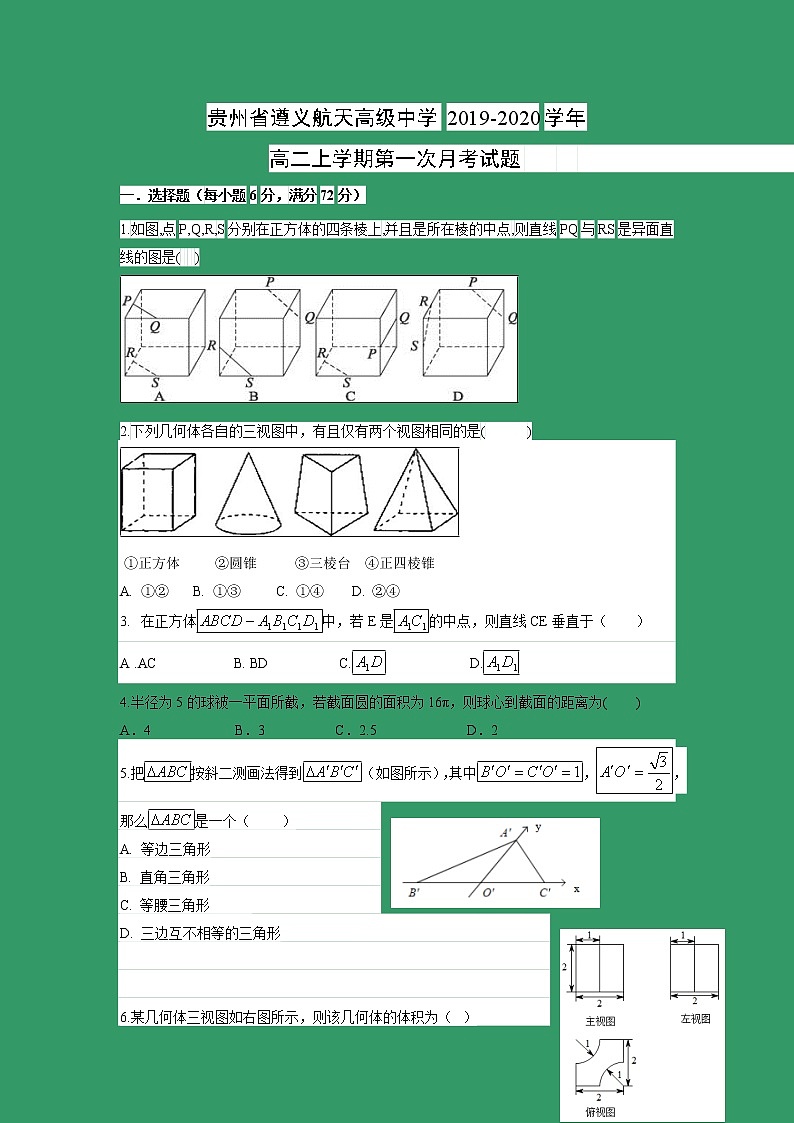
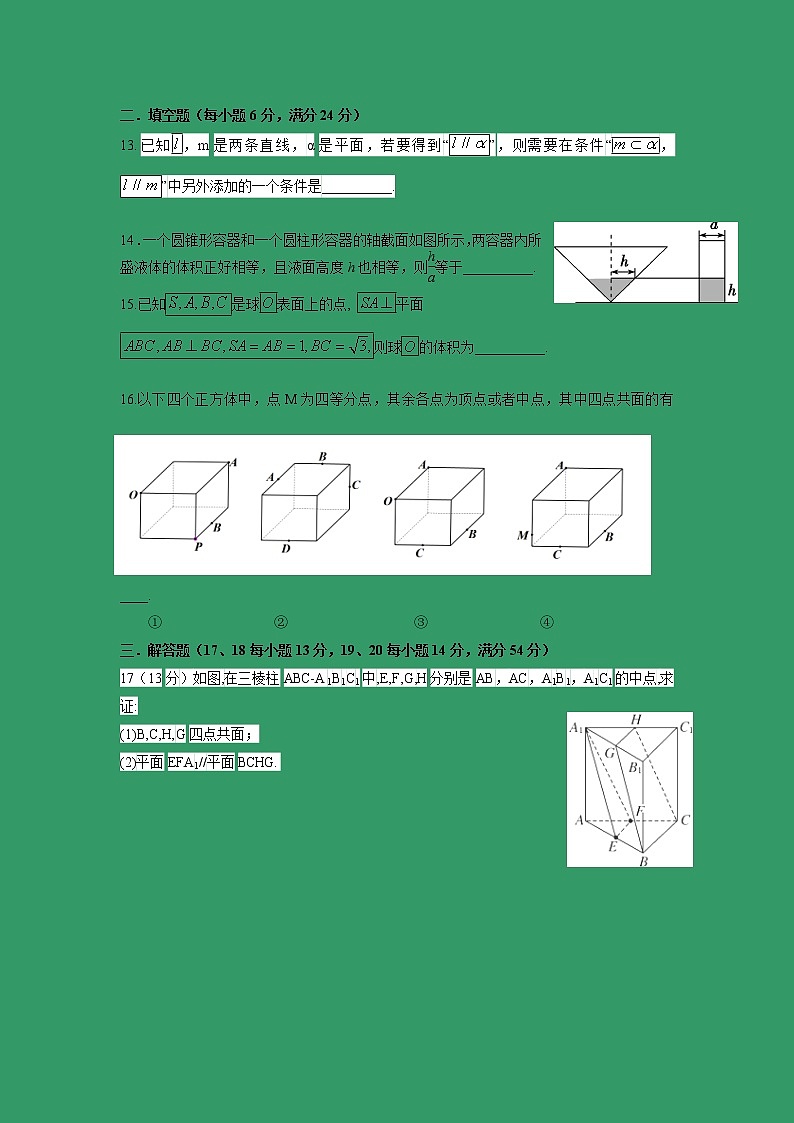
贵州省遵义航天高级中学2019-2020学年高二上学期第一次月考试题 一.选择题(每小题6分,满分72分)1.如图,点P,Q,R,S分别在正方体的四条棱上,并且是所在棱的中点,则直线PQ与RS是异面直线的图是( )2.下列几何体各自的三视图中,有且仅有两个视图相同的是( ) ①正方体 ②圆锥 ③三棱台 ④正四棱锥①② B. ①③ C. ①④ D. ②④ 在正方体中,若E是的中点,则直线CE垂直于( )A .AC B. BD C. D.4.半径为5的球被一平面所截,若截面圆的面积为16π,则球心到截面的距离为( )A.4 B.3 C.2.5 D.25.把按斜二测画法得到(如图所示),其中,,那么是一个( )A. 等边三角形B. 直角三角形C. 等腰三角形 D. 三边互不相等的三角形 6.某几何体三视图如右图所示,则该几何体的体积为( )A. B. C. D. 7.点分别是正方体的棱和的中点,则和所成角的大小为( )A. B. C. D. 8.如图,长方体与长方体的各个面所形成的二面角的大小中不正确的有( )A. B. C. D. 9.一个球与一个正三棱柱(底面为等边三角形,侧棱与底面垂直)的三个侧面和两个底面都相切,已知这个球的体积为 π,那么这个正三棱柱的体积是( )A. B. C. D.10.关于直线、b与平面α、β,有下列四个命题:①若∥α,b∥β且α∥β,则∥b ②若⊥α,b⊥β且α⊥β,则⊥b ③若⊥α,b∥β且α∥β,则⊥b ④若∥α,b⊥β且α⊥β,则∥b其中真命题的序号是( )A.①② B.②③ C.③④ D.①④11.如图所示是一几何体的平面展开图,其中四边形ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出以下四个结论:①直线BE与直线CF异面;②直线BE与直线AF异面;③直线EF//平面PBC;④平面BCE//平面PAD 其中正确的有( )A.1个 B.2个 C.3个 D.4个12.已知圆锥的顶点为S,母线SA,SB所成角的余弦值为,SA与圆锥底面所成角为,若的面积为,则该圆锥的侧面积为( )A.40 B. C. D.二.填空题(每小题6分,满分24分)已知,m是两条直线,α是平面,若要得到“”,则需要在条件“,”中另外添加的一个条件是__________.14.一个圆锥形容器和一个圆柱形容器的轴截面如图所示,两容器内所盛液体的体积正好相等,且液面高度h也相等,则等于__________.15.已知是球表面上的点, 平面则球的体积为__________.16.以下四个正方体中,点M为四等分点,其余各点为顶点或者中点,其中四点共面的有____.① ② ③ ④三.解答题(17、18每小题13分,19、20每小题14分,满分54分)17(13分)如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:
(1)B,C,H,G四点共面;
(2)平面EFA1//平面BCHG. 18(13分)如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC, E、F分别是PC、AD中点,(1)求证:DE// 平面PFB;(2)求PB与面PCD所成角的正切值。 19(15分)如图,AB是圆O的直径,C是圆O上不同于A,B的一点,PA⊥平面ABC,E是PC的中点, ,PA=AC=1.
(1)求证:AE⊥PB;
(2)求三棱锥C-ABE的距离.(3)求二面角A-PB-C的正弦值. 20(13分)如图,在矩形ABCD中,AB=2BC,P是线段AB中点,平面ABCD.
(1)求证:平面EPC;
(2)问在EP上是否存在点F,使平面平面BFC?若存在,求出的值;若不存在请说明理由.
参考答案一、选择题1-12、CDBBA CBBDB BA二、填空题 14. 15. 16.②三、解答题17、 18、 证明:(1)∵PA⊥平面ABC,BC⊂平面ABC
∴PA⊥BC,
又AB是圆O的直径,C是圆O上不同于A,B的一点
∴∠ACB=90°,即AC⊥BC,又PA∩AC=A
∴BC⊥平面PAC,又AE⊂平面PAC
∴BC⊥AE
∵PA=AC,E是PC的中点
∴AE⊥PC,又BC∩PC=C
∴AE⊥平面PBC,又PB⊂平面PBC ∴AE⊥PB.(2)VC-ABE=(3)过A作AF⊥PB交PB于F,连接EF
又由(1)得AE⊥PB,AE∩AF=A
∴PB⊥平面AEF,又EF⊂平面AEF
∴PB⊥EF,又AF⊥PB
∴∠AFE是二面角A-PB-C的平面角)
∵在Rt△PAC中,PA=AC=1,则 ,
在Rt△PAB中,PA=1, ,同理得
∴在Rt△AEF中,
故二面角A-PB-C的正弦值为 .20.





