

【数学】贵州省遵义市南白中学2019-2020学年高二上学期第三次月考(理) 试卷
展开
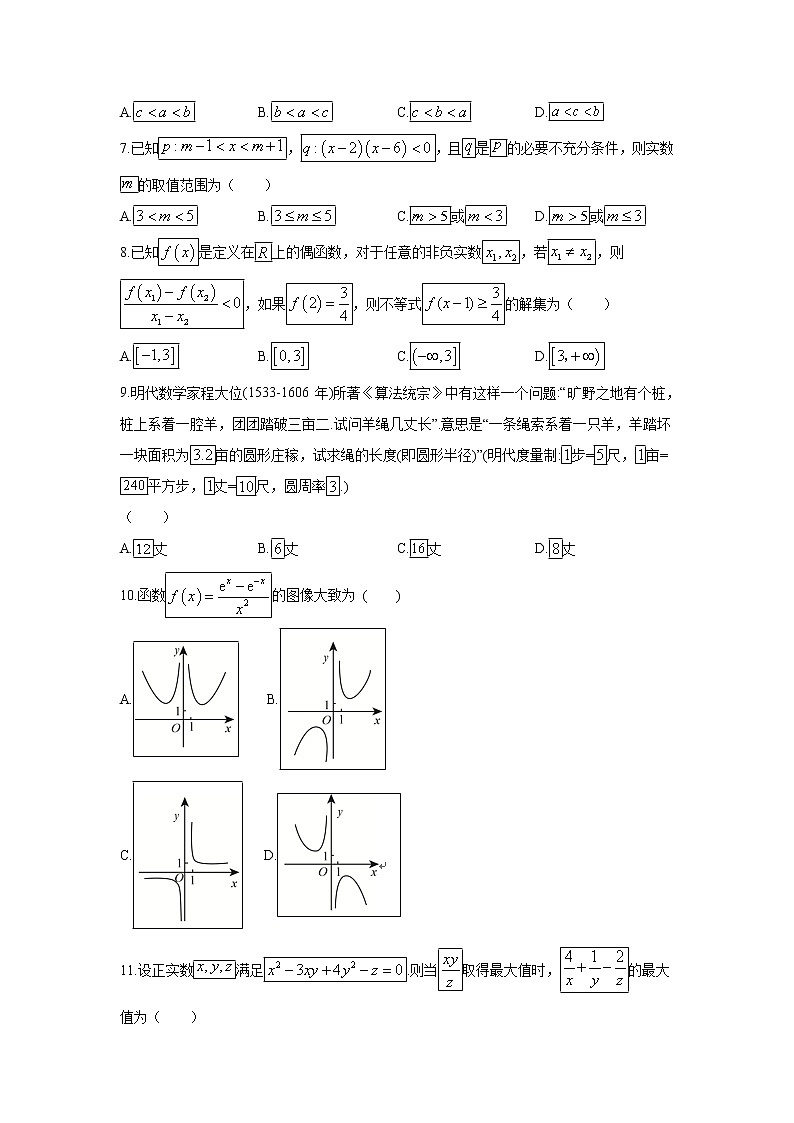
贵州省遵义市南白中学2019-2020学年高二上学期第三次月考(理)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.2.答题前,考生务必将自己的姓名,准考证号填写在本试题相应的位置.3.全部答案在答题卡上完成,答在本试题上无效.4.考试结束后,将本试题和答题卡一并交回.第Ⅰ卷(选择题)一、选择题:(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合,则( )A. B. C. D.2.己知等差数列中,,则( )A.7 B.8 C.14 D.163.椭圆的离心率为( )A. B. C. D.4.命题“”的否定为( )A. B.C. D.5.若一个正方体截去一个三棱锥后所得的几何体如图所示.则该几何体的正视图是( ) A. B. C. D.6.已知,,,则( ) A. B. C. D.7.已知,,且是的必要不充分条件,则实数的取值范围为( )A. B. C.或 D.或8.已知是定义在上的偶函数,对于任意的非负实数,若,则,如果,则不等式的解集为( )A. B. C. D.9.明代数学家程大位(1533-1606 年)所著《算法统宗》中有这样一个问题:“旷野之地有个桩,桩上系着一腔羊,团团踏破三亩二.试问羊绳几丈长”.意思是“一条绳索系着一只羊,羊踏坏一块面积为亩的圆形庄稼,试求绳的长度(即圆形半径)”(明代度量制:步=尺,亩=平方步,丈=尺,圆周率.)( )A.丈 B.丈 C.丈 D.丈10.函数的图像大致为 ( )A. B. C. D.11.设正实数满足.则当取得最大值时,的最大值为( )A.0 B.1 C. D.312.在四棱锥中,底面是边长为4的正方形,是一个正三角形,若平面平面,则该四棱锥的外接球的表面积为( )[来源:学科网]A. B. C. D.第Ⅱ卷(非选择题)二、填空题(本大题共4个小题,每小题5分,共20分,将答案填在答题纸上)13.向量,若,则实数 .14.的内角的对边分别为.若,则的面积为 .15.已知,分别为椭圆的左、右焦点,若直线上存在点,使为等腰三角形,则椭圆离心率的范围是 .16.已知为单位圆的一条弦,为单位圆上的点,若()的最小值为,当点在单位圆上运动时,的最大值为,则线段的长度为 .三、解答题 (本大题共6个小题,第17题10分,其余每个题12分,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在平面四边形中,,,,.(Ⅰ)求;(Ⅱ)若,求. 18.《中华人民共和国道路交通安全法》第条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第条规定:对不礼让行人的驾驶员处以扣分,罚款元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:月份[来源:学§科§网]违章驾驶员人数(Ⅰ)请利用所给数据求违章人数与月份之间的回归直线方程;(Ⅱ)预测该路口月份的不“礼让斑马线”违章驾驶员人数.参考公式: ,参考数据:. 19.已知等比数列的公比,且为,的等比中项,为,的等差中项.(1)求的值;(2)设数列的前项和为,求证: 20.如图,四棱锥中,平面,底面是正方形,且,为中点.(Ⅰ)求证:平面;(Ⅱ)求二面角的余弦值. 21.设是圆上的动点,点是在轴上的投影,且.(Ⅰ)当在圆上运动时,求点的轨迹的方程;(Ⅱ)求过点(1,0),倾斜角为的直线被所截线段的长度. 22.设椭圆,右顶点是,离心率为.(Ⅰ)求椭圆的方程;(Ⅱ)若直线与椭圆交于两点(不同于点),若,求证:直线过定点,并求出定点坐标.
参考答案一、选择题:(共12个小题,每小题5分,共60分)123456789101112CABDACBADBCD二、填空题:(共4个小题,每小题5分,共20分)13. 14. 15. 16.三、解答题:(共6个小题,共70分)17.(本大题10分)解:(Ⅰ)在中,由正弦定理得由题设知,,所以···············3分由题设知,,所以···························5分(2)由题设及(1)知,························7分在中,由余弦定理得.所以················································10分18.(本大题12分)解:(Ⅰ)由表中数据知, ,, ··········4分所求回归直线方程为···········································6分(2)令,则人该路口月份的不“礼让斑马线”违章驾驶员人数预计为49人····················12分19.(本大题12分)解:(1)由题意得则解得······5分(2)由题知,则.当时,···························7分当时,,故,综上所述,···············12分20.(本大题12分)解:(Ⅰ)证明:平面,又正方形中,,平面···················3分又平面,,,是的中点,平面······································6分(Ⅱ)以点为坐标原点,分别以直线为轴,轴,轴,建立如图所示的空间直角坐标系,由题意知:设平面的法向量为,则,,令,得到,····························8分又,且平面,平面的一个法向量为·································9分设二面角的平面角为则.二面角的余弦值为·······12分21.(本大题12分)解:(1)设的坐标为,的坐标为. 由,可得, 的坐标为,是圆上的动点 ··············································3分 ,坐标关系式为:代入得:整理可得的轨迹的方程: ·······························6分(Ⅱ)求过点,倾斜角为的直线方程为: 设直线与轨迹的交点为 将直线方程与轨迹方程联立方程组,消掉 得: ,整理可得: 根据韦达定理得: ······························9分线段AB的长度为: ······························12分22.(本大题12分)解:(Ⅰ)右顶点是,离心率为,所以,∴,则····3分椭圆的标准方程为··············································5分(Ⅰ)当直线斜率不存在时,设与椭圆方程联立得:,设直线与轴交于点,,即或 (舍),直线过定点·························6分当直线斜率存在时,设直线斜率为,,则直线与椭圆方程联立,得,·················································8分,,,则,即,,或····························································10分直线或直线过定点或舍去;综上知直线过定点··························12分





