还剩18页未读,
继续阅读
【数学】安徽省合肥一六八中学、铜陵一中等四校2019-2020学年高二上学期开学联考 试卷
展开
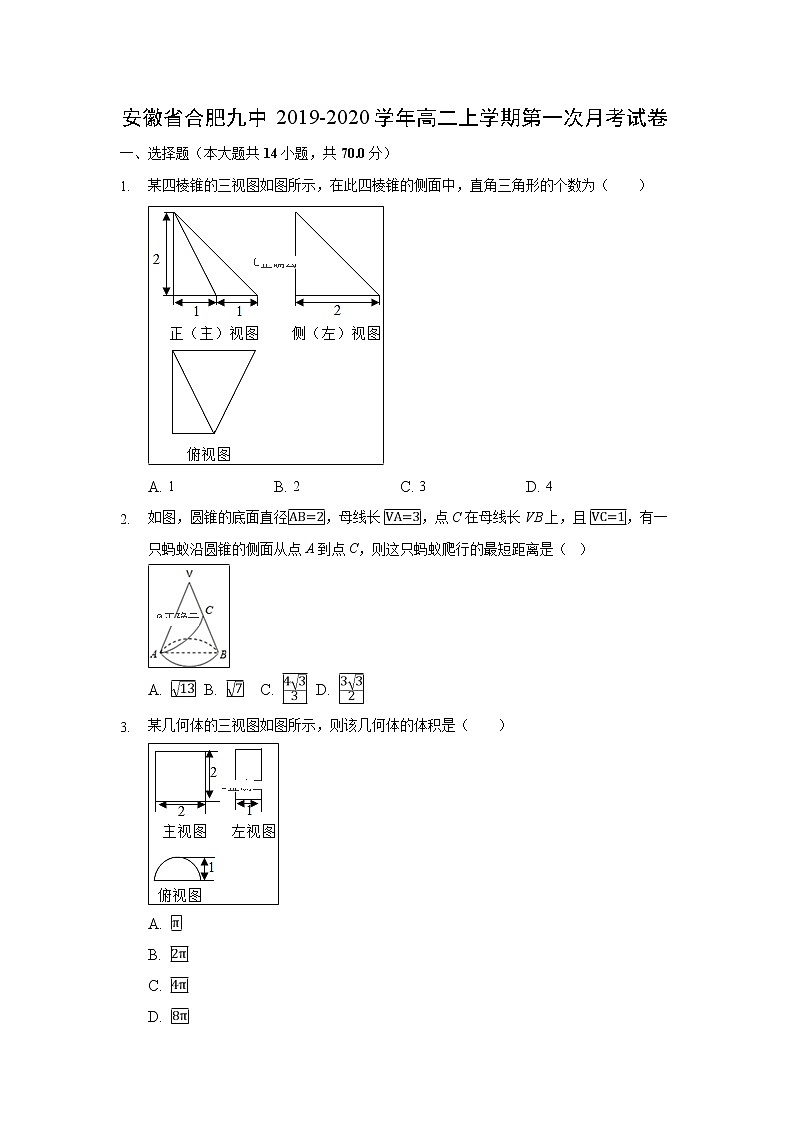
安徽省合肥九中2019-2020学年高二上学期第一次月考试卷
一、选择题(本大题共14小题,共70.0分)
1. 某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )
A. 1 B. 2 C. 3 D. 4
2. 如图,圆锥的底面直径,母线长 ,点C在母线长VB上,且 ,有一只蚂蚁沿圆锥的侧面从点A到点C,则这只蚂蚁爬行的最短距离是( )
A. B. C. D.
3. 某几何体的三视图如图所示,则该几何体的体积是( )
A.
B.
C.
D.
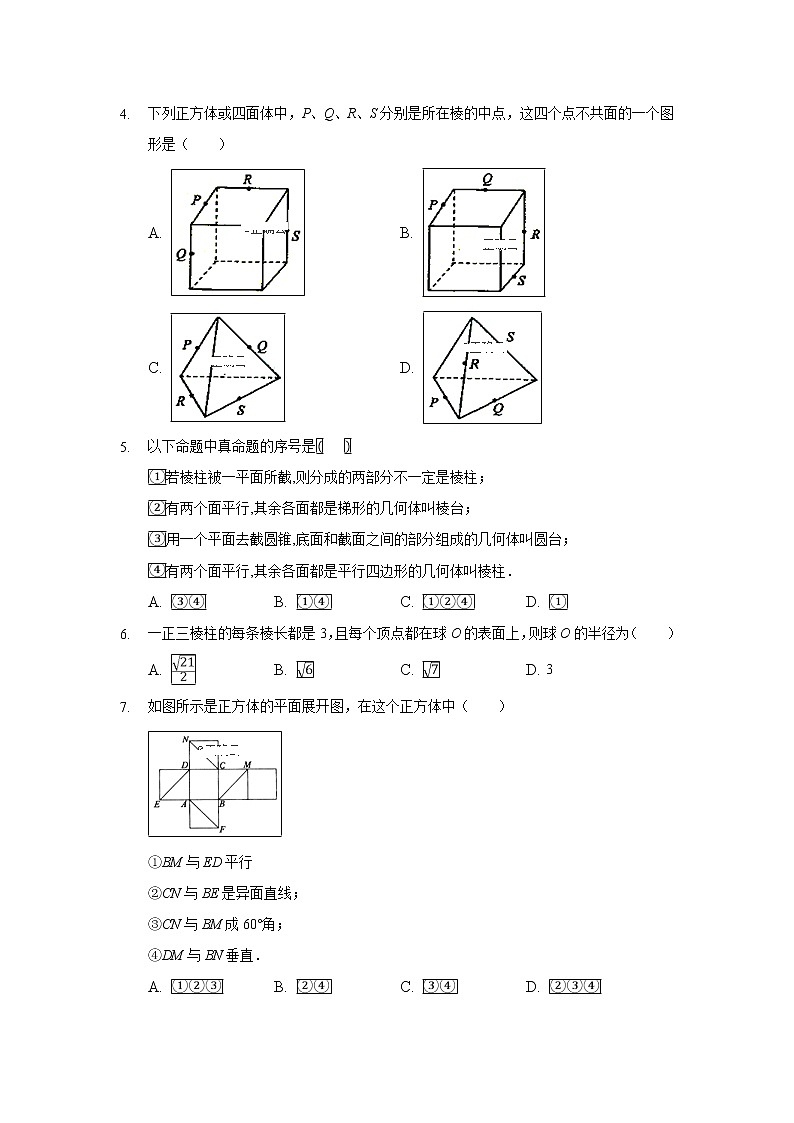
4. 下列正方体或四面体中,P、Q、R、S分别是所在棱的中点,这四个点不共面的一个图形是( )
A. B.
C. D.
5. 以下命题中真命题的序号是
若棱柱被一平面所截,则分成的两部分不一定是棱柱;
有两个面平行,其余各面都是梯形的几何体叫棱台;
用一个平面去截圆锥,底面和截面之间的部分组成的几何体叫圆台;
有两个面平行,其余各面都是平行四边形的几何体叫棱柱.
A. B. C. D.
6. 一正三棱柱的每条棱长都是3,且每个顶点都在球O的表面上,则球O的半径为( )
A. B. C. D. 3
7. 如图所示是正方体的平面展开图,在这个正方体中( )
①BM与ED平行
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
A. B. C. D.
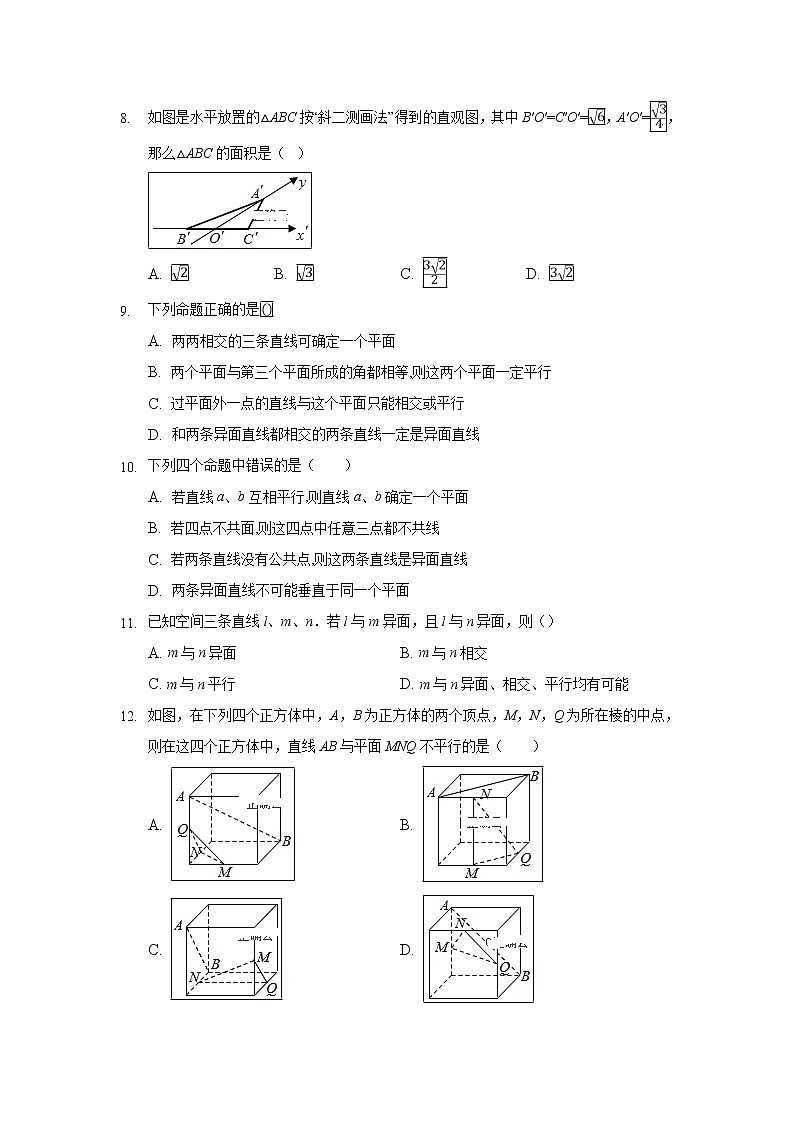
8. 如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=,A′O′=,那么△ABC的面积是( )
A. B. C. D.
9. 下列命题正确的是
A. 两两相交的三条直线可确定一个平面
B. 两个平面与第三个平面所成的角都相等,则这两个平面一定平行
C. 过平面外一点的直线与这个平面只能相交或平行
D. 和两条异面直线都相交的两条直线一定是异面直线
10. 下列四个命题中错误的是( )
A. 若直线a、b互相平行,则直线a、b确定一个平面
B. 若四点不共面,则这四点中任意三点都不共线
C. 若两条直线没有公共点,则这两条直线是异面直线
D. 两条异面直线不可能垂直于同一个平面
11. 已知空间三条直线l、m、n.若l与m异面,且l与n异面,则()
A. m与n异面 B. m与n相交
C. m与n平行 D. m与n异面、相交、平行均有可能
12. 如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
A. B.
C. D.
13. 下列命题,能得出直线m与平面α平行的是( )
A. 直线m与平面内 所有直线平行
B. 直线m 与平面内无数条直线平行
C. 直线m与平面没有公共点
D. 直线m与平面内的一条直线平行
14. 已知直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )
A. B. C. D.
二、填空题(本大题共4小题,共20.0分)
15. 如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则的值是______.
16. 如图,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A-DED1的体积为______.
17. 如图,已知三棱锥A-BCD中,AD,BD,CD两两垂直,AD=BD=1,CD=,E,F分别为AC,BC的中点,则点C到平面DEF的距离为__________ .
18. 如图所示,O是正方体ABCD-A1B1C1D1对角线A1C与AC1的交点,E为棱BB1的中点,则空间四边形OEC1D1在正方体各面上的投影不可能是___________ .
三、解答题(本大题共5小题,共60.0分)
19. 如图,是一个几何体的三视图,正视图和侧视图都是由一个边长为2的等边三角形和一个长为2宽为1的矩形组成.
(1)求该几何体的体积;
(2)求该几何体的表面积.
20. 如图,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形.
(1)证明:A1C1∥平面ACD1;
(2)求异面直线CD与AD1所成角的大小;
(3)已知三棱锥D1-ACD的体积为,求AA1的长.
21. 如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=,AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
22. 如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A、D分别是BF、CE上的点,AD∥BC,且DE=2AF=2AD(如图1).将四边形ADEF沿AD折起,使点E到达点G的位置,连结BG、BF、CG(如图2),且AB⊥GD.
(1)证明:AC∥平面BFG;
(2)当AB=DG=2,求三棱锥A-BCG的体积.
23. 如图,正方体中,是的中点.
(1)求证:平面;
(2)求异面直线与所成的角.
参考答案
1.【答案】C
【解析】解:四棱锥的三视图对应的直观图为:PA⊥底面ABCD,
AC=,CD=,
PC=3,PD=2,可得三角形PCD不是直角三角形.
所以侧面中有3个直角三角形,分别为:△PAB,△PBC,
△PAD.
故选:C.
画出三视图的直观图,判断各个面的三角形的情况,即可推出结果.
本题考查简单几何体的三视图的应用,是基本知识的考查.
2.【答案】B
【解析】【分析】
本题考查平面展开-最短路径问题,属于基础题.
要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.
圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
【解答】
解:由题意知,底面圆的直径为2,故底面周长等于2π,
设圆锥的侧面展开后的扇形圆心角为α,
根据底面周长等于展开后扇形的弧长得,2π=3α,
解得:α=,
∴∠AVA′=,
则∠1=,
过C作CF⊥VA,
∵VC=1,∠1=60°,
∴∠VCF=30°,
∴FV=,
∴CF2=CV2-VF2=,
∵AV=3,FV=,
∴AF=,
在Rt△AFC中,利用勾股定理得:AC2=AF2+FC2=7,
则AC=.
故选B.
3.【答案】A
【解析】【分析】
由三视图可知,该几何体为底面直径为2,高为2的圆柱的一半,求出体积即可.
本题的考点是由三视图求几何体的体积,需要由三视图判断空间几何体的结构特征,并根据三视图求出每个几何体中几何元素的长度,代入对应的体积公式分别求解,考查了空间想象能力.
【解答】
解:由三视图可知,该几何体为底面直径为2,高为2的圆柱的一半.
体积V==π.
故选A.
4.【答案】D
【解析】【分析】
在A、C中,均得到PR∥SQ,B中得到PS∥RQ,P、Q、R、S四点共面;在D中,PS与SQ既不平行也不相交,P、Q、R、S四点不共面.
本题考查四点共面的判断,是基础题,解题时要认真审题,注意平面的基本性质及推论的合理运用.
【解答】
解:在A中,∵正方体中,P、Q、R、S分别是所在棱的中点,
∴PR∥SQ,∴P、Q、R、S四点共面,故A不正确;
在B中,正方体中,P、Q、R、S分别是所在棱的中点,
∴PS∥RQ,∴P、Q、R、S四点共面,故B不正确;
在C中,四面体中,P、Q、R、S分别是所在棱的中点,
∴PR∥SQ,∴P、Q、R、S四点共面,故C不正确;
在D中,四面体中,P、Q、R、S分别是所在棱的中点,
∴PS与SQ既不平行也不相交,∴P、Q、R、S四点不共面,故D正确.
故选:D.
5.【答案】D
【解析】【分析】
本题考查棱柱、棱台、圆台的定义的应用,直接利用棱柱、棱台、圆台的定义,判断选项即可得出,是基础题.
【解答】
解:①若棱柱被一平面所截,则分成的两部分不一定是棱柱;正确,当平面与棱柱的所有平面不平行时,截出的两个几何体不是棱柱.
②有两个面平行,其余各面都是梯形的几何体叫棱台;不正确,不满足棱台的定义.
③用一个平面去截圆锥,底面和截面之间的部分组成的几何体叫圆台;不正确,当平面与底面平行时,底面和截面之间的部分组成的几何体叫圆台.
④有两个面平行,其余各面都是平行四边形的几何体叫棱柱.不正确,不满足棱柱的定义.如下图:
故选D.
6.【答案】A
【解析】【分析】
本题考查正三棱柱的外接球的半径的求法,明确球心、球的半径与正三棱柱的关系是本题解决的关键.正三棱柱的两个底面的中心的连线的中点就是球的球心,球心与顶点的连线长就是半径,利用勾股定理求出球的半径.
【解答】
解:正三棱柱的两个底面的中心的连线的中点就是球的球心,球心与顶点的连线长就是半径,
所以,r==.
故选A.
7.【答案】C
【解析】【分析】
本题考查正方体的结构特征,异面直线,直线与直线所成的角,直线与直线的垂直,是基础题.
正方体的平面展开图复原为正方体,不难解答本题.
【解答】
解:由题意画出正方体的图形如图:
显然①②不正确;
③CN与BM成60°角,即∠ANC=60°正确;
④DM⊥平面BCN,所以④正确.
故选C.
8.【答案】C
【解析】【分析】
本题考查斜二测画法中原图和直观图面积之间的关系,属基本运算的考查.B′O′=C′O′=,A′O′=,直接计算△ABC即可.
【解答】
解:因为B′O′=C′O′=,A′O′=,
所以△ABC的面积为=.
故选C.
9.【答案】C
【解析】【分析】
本题考查了空间中的直线与平面的位置关系以及平面的基本性质应用问题,是基础题目.
根据空间中的直线与平面的位置关系以及平面的基本性质,对选项中的命题判断正误即可.
【解答】
解:对于A,两两相交的三条直线可确定一个平面或三个平面,故A错误;
对于B,两个平面与第三个平面所成的角都相等,则这两个平面平行或相交,故B错误;
对于C,过平面外一点的直线一定在平面外,且直线与这个平面相交或平行,故C正确;
对于D,和两条异面直线都相交的两条直线是异面直线或共面直线,故D错误.
故选C.
10.【答案】C
【解析】【分析】
本题主要考查公理2以及推论、由线线位置关系的定义、线面垂直的性质定理和异面直线的定义,难度不大,需要掌握好基本知识.
【解答】
解:A、由两条直线平行确定一个平面判断正确,故A不对;
B、根据三棱锥的四个顶点知,任意三点都不共线,故B不对;
C、若两条直线没有公共点,则这两条直线异面或平行,故C对;
D、根据线面垂直的性质定理知,这两条直线平行,即不可能,故D不对.
故选C.
11.【答案】D
【解析】【分析】
可根据题目中的信息作图判断即可.
本题考查平面的基本性质,着重考查学生的理解与转化能力,考查数形结合思想,属于基础题.
【解答】解:∵空间三条直线l、m、n.若l与m异面,且l与n异面,
∵m与n可能异面(如图3),也可能平行(图1),也可能相交(图2),
故选D.
12.【答案】A
【解析】【分析】
本题考查空间中线面平行的判定定理,利用三角形中位线定理是解决本题的关键,注意解题方法的积累,属于中档题.利用线面平行判定定理可知B、C、D均不满足题意,从而可得答案.
【解答】
解:对于选项B,由于AB∥MQ,结合线面平行判定定理可知AB//平面MNQ,故B不满足题意;
对于选项C,由于AB∥MQ,结合线面平行判定定理可知AB//平面MNQ,故C不满足题意;
对于选项D,由于AB∥NQ,结合线面平行判定定理可知AB//平面MNQ,故D不满足题意;
选项A满足题意,(假设AB//平面MNQ,利用线面平行的性质定理,过ABQ的平面与MN交点P,可得AB//QP,但QP显然与AB不平行,矛盾,所以直线AB与平面MNQ不平行.)
故选A.
13.【答案】C
【解析】【分析】
本题主要考查了直线与平面平行的判定.利用特例解决选择题,较好.判断出A项说法错误,B项,C项当直线m在平面α内,满足,但m与α不平行.
【解答】
解:A项命题本身说法错误;
B项当直线m在平面α内,m与α不平行;
C项能推出m与α平行.
D项,当直线m在平面α内满足,m与α不平行.
故选C.
14.【答案】C
【解析】【分析】
本题考查了空间中的两条异面直线所成角的计算问题,也考查了空间中的平行关系应用问题,是中档题.设M、N、P分别为AB,BB1和B1C1的中点,得出AB1、BC1夹角为MN和NP夹角或其补角;根据中位线定理,结合余弦定理求出AC、MQ,MP和∠MNP的余弦值即可.
【解答】
解:如图所示,设M、N、P分别为AB,BB1和B1C1的中点,
则AB1、BC1夹角为MN和NP夹角或其补角(因异面直线所成角为(0,]),
可知MN=AB1=,NP=BC1=;
作BC中点Q,则△PQM为直角三角形,PQ=1,MQ=AC,
△ABC中,由余弦定理得AC2=AB2+BC2-2AB•BC•cos∠ABC=4+1-2×2×1×(-)=7,
∴AC=,∴MQ=,MP==;
在△PMN中,由余弦定理得cos∠MNP===-;
又异面直线所成角的范围是(0,],∴AB1与BC1所成角的余弦值为.
故选C.
15.【答案】
【解析】【分析】
本题考查球的体积以及圆柱的体积的求法,考查空间想象能力以及计算能力.
设出球的半径,求出圆柱的体积以及球的体积即可得到结果.
【解答】
解:设球的半径为R,则球的体积为V2=R3,
圆柱的体积为V1=πR2•2R=2πR3,
则==.
故答案为.
16.【答案】
【解析】解:将三棱锥A-DED1选择△ADD1为底面,E为顶点,则VA -DED1=VE -ADD1,
其中S△ADD1=SA1D1DA=,E到底面ADD1的距离等于棱长1,
故.
故答案为:
将三棱锥A-DED1选择△ADD1为底面,E为顶点,进行等体积转化VA -DED1=VE -ADD1后体积易求
本题考查了三棱柱体积的计算,等体积转化法是常常需要优先考虑的策略.
17.【答案】
【解析】【分析】
此题考查点到面的距离,考查线面垂直的判断,及三棱锥的体积公式,属于中档题.
关键是利用体积相等列方程.
【解答】
解:三棱锥A-BCD中,AD,BD,CD两两垂直,
则,
点A到平面BDC的距离为AD=1,
E为AC的中点,
则点E到平面DFC的距离为,
又,,
,,
由余弦定理可得,在中,有
所以,
设点C到平面DEF的距离为d,
又,
,
所以.
故答案为.
18.【答案】①
【解析】【分析】
空间四边形OEC1D1在正方体左右面上的投影是③选项的图形,空间四边形OEC1D1在正方体上下面上的投影是④选项的图形,空间四边形OEC1D1在正方体前后面上的投影是②选项的图形,得到结论.
本题考查平行投影及平行投影作图法,考查在同一图形在不同投影面上的投影不同,本题是一个基础题.
【解答】
解:空间四边形OEC1D1在正方体左右面上的投影是③选项的图形,
空间四边形OEC1D1在正方体上下面上的投影是④选项的图形,
空间四边形OEC1D1在正方体前后面上的投影是②选项的图形,
只有①选项不可能是投影,
故答案为:①.
19.【答案】解:(1)由三视图知,该三视图对应的几何体为一个底面直径为2,母线长为2的圆锥与一个长宽都为2高为1的长方体组成的组合体.
此几何体的体积为;
(2)此几何体的表面积.
【解析】本题主要考查空间几何体的三视图以及几何体的表面积与体积,考查了学生的空间想象能力,培养了学生分析问题与解决问题的能力.
(1)根据空间几何体的三视图,可知原几何体的形状,利用柱体与圆锥的体积即可求得结果;
(2)利用柱体与圆锥的即可得到结果.
20.【答案】(1)证明:在长方体中,因A1A=CC1,A1A∥CC1,可得A1C1∥AC,
A1C1不在平面ACD1内,AC⊂平面ACD1,
则A1C1∥平面ACD1;……………………………………………(4分)
(2)解:因为CD⊥平面ADD1A1,AD1⊂平面ADD1A1,可得CD⊥AD1,
所以异面直线CD与AD1所成角900; ………………………………………………(8分)
(3)解:由三棱锥D1-ACD的体积为,可得,
∴AA1=1.……………………………………………(12分)
【解析】(1)根据直线与平面平行的判定定理可知只需证A1C1∥AC,即可得A1C1∥平面ACD1;
(2)由CD⊥平面ADD1A1,可得CD⊥AD1,异面直线CD与AD1所成角900;
(3)由三棱锥D1-ACD的体积为,可得,即可得解.
本题考查直线与平面平行的判定,直线与直线所成角的计算,考查学生空间想象能力,逻辑思维能力,是中档题.
21.【答案】解:四边形ABCD绕AD旋转一周所成的
几何体,如右图:
S表面=S圆台下底面+S圆台侧面+S圆锥侧面
=πr22+π(r1+r2)l2+πr1l1
=
=
=.
体积V=V圆台-V圆锥
=[25π++4π]×4-×2π×2×2
=×39π×4-×8π
=.
所求表面积为:,体积为:.
【解析】旋转后的几何体是圆台除去一个倒放的圆锥,根据题目所给数据,求出圆台的侧面积、圆锥的侧面积、圆台的底面积,即可求出几何体的表面积.求出圆台体积减去圆锥体积,即可得到几何体的体积.
本题是基础题,考查旋转体的表面积与体积,转化思想的应用,计算能力的考查,都是为本题设置的障碍,仔细分析旋转体的结构特征,为顺利解题创造依据.
22.【答案】(1)证明:取DG中点M,连接AM,CM,
可得AM∥FG,CM∥BF,
又AM∩CM=M,
∴平面ACM∥平面BFG,
∴AC∥平面BFG;
(2)解:由AB⊥DG,AD⊥DG,且AB∩AD=A,
可得DG⊥平面ABCD,
又AB=DG=2,
∴,
∴.
【解析】(1)取DG中点M,连接AM,CM,得AM∥FG,CM∥BF,由面面平行的判定可得平面ACM∥平面BFG,进一步得到AC∥平面BFG;
(2)由AB⊥DG,AD⊥DG,得DG⊥平面ABCD,由已知结合棱锥体积公式可得三棱锥A-BCG的体积.
本题考查直线与平面平行的判定,考查空间想象能力与思维能力,训练了多面体体积的求法,是中档题.
23.【答案】(1)证明:连接交于点,连接.
因为分别是与的中点,
所以.
又因为在平面内,不在平面内,
所以平面.
(2)解:连接,
由于且,
所以四边形为平行四边形,,
异面直线与所成的角为或其补角.
而为正三角形,
所以异面直线与所成的角为.
【解析】本题主要考查空间中的线面关系的证明及异面直线所成角的求法,考查线面垂直判定定理及平面向量的夹角求异面直线所成角,属于中档题.
(1)连结交于点,连结,再运用线面平行的判定方法化简即可求解;
(2)由题意得,直接运用线线角的判定方法化简即可求解.
一、选择题(本大题共14小题,共70.0分)
1. 某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )
A. 1 B. 2 C. 3 D. 4
2. 如图,圆锥的底面直径,母线长 ,点C在母线长VB上,且 ,有一只蚂蚁沿圆锥的侧面从点A到点C,则这只蚂蚁爬行的最短距离是( )
A. B. C. D.
3. 某几何体的三视图如图所示,则该几何体的体积是( )
A.
B.
C.
D.
4. 下列正方体或四面体中,P、Q、R、S分别是所在棱的中点,这四个点不共面的一个图形是( )
A. B.
C. D.
5. 以下命题中真命题的序号是
若棱柱被一平面所截,则分成的两部分不一定是棱柱;
有两个面平行,其余各面都是梯形的几何体叫棱台;
用一个平面去截圆锥,底面和截面之间的部分组成的几何体叫圆台;
有两个面平行,其余各面都是平行四边形的几何体叫棱柱.
A. B. C. D.
6. 一正三棱柱的每条棱长都是3,且每个顶点都在球O的表面上,则球O的半径为( )
A. B. C. D. 3
7. 如图所示是正方体的平面展开图,在这个正方体中( )
①BM与ED平行
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
A. B. C. D.
8. 如图是水平放置的△ABC按“斜二测画法”得到的直观图,其中B′O′=C′O′=,A′O′=,那么△ABC的面积是( )
A. B. C. D.
9. 下列命题正确的是
A. 两两相交的三条直线可确定一个平面
B. 两个平面与第三个平面所成的角都相等,则这两个平面一定平行
C. 过平面外一点的直线与这个平面只能相交或平行
D. 和两条异面直线都相交的两条直线一定是异面直线
10. 下列四个命题中错误的是( )
A. 若直线a、b互相平行,则直线a、b确定一个平面
B. 若四点不共面,则这四点中任意三点都不共线
C. 若两条直线没有公共点,则这两条直线是异面直线
D. 两条异面直线不可能垂直于同一个平面
11. 已知空间三条直线l、m、n.若l与m异面,且l与n异面,则()
A. m与n异面 B. m与n相交
C. m与n平行 D. m与n异面、相交、平行均有可能
12. 如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
A. B.
C. D.
13. 下列命题,能得出直线m与平面α平行的是( )
A. 直线m与平面内 所有直线平行
B. 直线m 与平面内无数条直线平行
C. 直线m与平面没有公共点
D. 直线m与平面内的一条直线平行
14. 已知直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )
A. B. C. D.
二、填空题(本大题共4小题,共20.0分)
15. 如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则的值是______.
16. 如图,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A-DED1的体积为______.
17. 如图,已知三棱锥A-BCD中,AD,BD,CD两两垂直,AD=BD=1,CD=,E,F分别为AC,BC的中点,则点C到平面DEF的距离为__________ .
18. 如图所示,O是正方体ABCD-A1B1C1D1对角线A1C与AC1的交点,E为棱BB1的中点,则空间四边形OEC1D1在正方体各面上的投影不可能是___________ .
三、解答题(本大题共5小题,共60.0分)
19. 如图,是一个几何体的三视图,正视图和侧视图都是由一个边长为2的等边三角形和一个长为2宽为1的矩形组成.
(1)求该几何体的体积;
(2)求该几何体的表面积.
20. 如图,在长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形.
(1)证明:A1C1∥平面ACD1;
(2)求异面直线CD与AD1所成角的大小;
(3)已知三棱锥D1-ACD的体积为,求AA1的长.
21. 如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=,AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
22. 如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A、D分别是BF、CE上的点,AD∥BC,且DE=2AF=2AD(如图1).将四边形ADEF沿AD折起,使点E到达点G的位置,连结BG、BF、CG(如图2),且AB⊥GD.
(1)证明:AC∥平面BFG;
(2)当AB=DG=2,求三棱锥A-BCG的体积.
23. 如图,正方体中,是的中点.
(1)求证:平面;
(2)求异面直线与所成的角.
参考答案
1.【答案】C
【解析】解:四棱锥的三视图对应的直观图为:PA⊥底面ABCD,
AC=,CD=,
PC=3,PD=2,可得三角形PCD不是直角三角形.
所以侧面中有3个直角三角形,分别为:△PAB,△PBC,
△PAD.
故选:C.
画出三视图的直观图,判断各个面的三角形的情况,即可推出结果.
本题考查简单几何体的三视图的应用,是基本知识的考查.
2.【答案】B
【解析】【分析】
本题考查平面展开-最短路径问题,属于基础题.
要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.
圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
【解答】
解:由题意知,底面圆的直径为2,故底面周长等于2π,
设圆锥的侧面展开后的扇形圆心角为α,
根据底面周长等于展开后扇形的弧长得,2π=3α,
解得:α=,
∴∠AVA′=,
则∠1=,
过C作CF⊥VA,
∵VC=1,∠1=60°,
∴∠VCF=30°,
∴FV=,
∴CF2=CV2-VF2=,
∵AV=3,FV=,
∴AF=,
在Rt△AFC中,利用勾股定理得:AC2=AF2+FC2=7,
则AC=.
故选B.
3.【答案】A
【解析】【分析】
由三视图可知,该几何体为底面直径为2,高为2的圆柱的一半,求出体积即可.
本题的考点是由三视图求几何体的体积,需要由三视图判断空间几何体的结构特征,并根据三视图求出每个几何体中几何元素的长度,代入对应的体积公式分别求解,考查了空间想象能力.
【解答】
解:由三视图可知,该几何体为底面直径为2,高为2的圆柱的一半.
体积V==π.
故选A.
4.【答案】D
【解析】【分析】
在A、C中,均得到PR∥SQ,B中得到PS∥RQ,P、Q、R、S四点共面;在D中,PS与SQ既不平行也不相交,P、Q、R、S四点不共面.
本题考查四点共面的判断,是基础题,解题时要认真审题,注意平面的基本性质及推论的合理运用.
【解答】
解:在A中,∵正方体中,P、Q、R、S分别是所在棱的中点,
∴PR∥SQ,∴P、Q、R、S四点共面,故A不正确;
在B中,正方体中,P、Q、R、S分别是所在棱的中点,
∴PS∥RQ,∴P、Q、R、S四点共面,故B不正确;
在C中,四面体中,P、Q、R、S分别是所在棱的中点,
∴PR∥SQ,∴P、Q、R、S四点共面,故C不正确;
在D中,四面体中,P、Q、R、S分别是所在棱的中点,
∴PS与SQ既不平行也不相交,∴P、Q、R、S四点不共面,故D正确.
故选:D.
5.【答案】D
【解析】【分析】
本题考查棱柱、棱台、圆台的定义的应用,直接利用棱柱、棱台、圆台的定义,判断选项即可得出,是基础题.
【解答】
解:①若棱柱被一平面所截,则分成的两部分不一定是棱柱;正确,当平面与棱柱的所有平面不平行时,截出的两个几何体不是棱柱.
②有两个面平行,其余各面都是梯形的几何体叫棱台;不正确,不满足棱台的定义.
③用一个平面去截圆锥,底面和截面之间的部分组成的几何体叫圆台;不正确,当平面与底面平行时,底面和截面之间的部分组成的几何体叫圆台.
④有两个面平行,其余各面都是平行四边形的几何体叫棱柱.不正确,不满足棱柱的定义.如下图:
故选D.
6.【答案】A
【解析】【分析】
本题考查正三棱柱的外接球的半径的求法,明确球心、球的半径与正三棱柱的关系是本题解决的关键.正三棱柱的两个底面的中心的连线的中点就是球的球心,球心与顶点的连线长就是半径,利用勾股定理求出球的半径.
【解答】
解:正三棱柱的两个底面的中心的连线的中点就是球的球心,球心与顶点的连线长就是半径,
所以,r==.
故选A.
7.【答案】C
【解析】【分析】
本题考查正方体的结构特征,异面直线,直线与直线所成的角,直线与直线的垂直,是基础题.
正方体的平面展开图复原为正方体,不难解答本题.
【解答】
解:由题意画出正方体的图形如图:
显然①②不正确;
③CN与BM成60°角,即∠ANC=60°正确;
④DM⊥平面BCN,所以④正确.
故选C.
8.【答案】C
【解析】【分析】
本题考查斜二测画法中原图和直观图面积之间的关系,属基本运算的考查.B′O′=C′O′=,A′O′=,直接计算△ABC即可.
【解答】
解:因为B′O′=C′O′=,A′O′=,
所以△ABC的面积为=.
故选C.
9.【答案】C
【解析】【分析】
本题考查了空间中的直线与平面的位置关系以及平面的基本性质应用问题,是基础题目.
根据空间中的直线与平面的位置关系以及平面的基本性质,对选项中的命题判断正误即可.
【解答】
解:对于A,两两相交的三条直线可确定一个平面或三个平面,故A错误;
对于B,两个平面与第三个平面所成的角都相等,则这两个平面平行或相交,故B错误;
对于C,过平面外一点的直线一定在平面外,且直线与这个平面相交或平行,故C正确;
对于D,和两条异面直线都相交的两条直线是异面直线或共面直线,故D错误.
故选C.
10.【答案】C
【解析】【分析】
本题主要考查公理2以及推论、由线线位置关系的定义、线面垂直的性质定理和异面直线的定义,难度不大,需要掌握好基本知识.
【解答】
解:A、由两条直线平行确定一个平面判断正确,故A不对;
B、根据三棱锥的四个顶点知,任意三点都不共线,故B不对;
C、若两条直线没有公共点,则这两条直线异面或平行,故C对;
D、根据线面垂直的性质定理知,这两条直线平行,即不可能,故D不对.
故选C.
11.【答案】D
【解析】【分析】
可根据题目中的信息作图判断即可.
本题考查平面的基本性质,着重考查学生的理解与转化能力,考查数形结合思想,属于基础题.
【解答】解:∵空间三条直线l、m、n.若l与m异面,且l与n异面,
∵m与n可能异面(如图3),也可能平行(图1),也可能相交(图2),
故选D.
12.【答案】A
【解析】【分析】
本题考查空间中线面平行的判定定理,利用三角形中位线定理是解决本题的关键,注意解题方法的积累,属于中档题.利用线面平行判定定理可知B、C、D均不满足题意,从而可得答案.
【解答】
解:对于选项B,由于AB∥MQ,结合线面平行判定定理可知AB//平面MNQ,故B不满足题意;
对于选项C,由于AB∥MQ,结合线面平行判定定理可知AB//平面MNQ,故C不满足题意;
对于选项D,由于AB∥NQ,结合线面平行判定定理可知AB//平面MNQ,故D不满足题意;
选项A满足题意,(假设AB//平面MNQ,利用线面平行的性质定理,过ABQ的平面与MN交点P,可得AB//QP,但QP显然与AB不平行,矛盾,所以直线AB与平面MNQ不平行.)
故选A.
13.【答案】C
【解析】【分析】
本题主要考查了直线与平面平行的判定.利用特例解决选择题,较好.判断出A项说法错误,B项,C项当直线m在平面α内,满足,但m与α不平行.
【解答】
解:A项命题本身说法错误;
B项当直线m在平面α内,m与α不平行;
C项能推出m与α平行.
D项,当直线m在平面α内满足,m与α不平行.
故选C.
14.【答案】C
【解析】【分析】
本题考查了空间中的两条异面直线所成角的计算问题,也考查了空间中的平行关系应用问题,是中档题.设M、N、P分别为AB,BB1和B1C1的中点,得出AB1、BC1夹角为MN和NP夹角或其补角;根据中位线定理,结合余弦定理求出AC、MQ,MP和∠MNP的余弦值即可.
【解答】
解:如图所示,设M、N、P分别为AB,BB1和B1C1的中点,
则AB1、BC1夹角为MN和NP夹角或其补角(因异面直线所成角为(0,]),
可知MN=AB1=,NP=BC1=;
作BC中点Q,则△PQM为直角三角形,PQ=1,MQ=AC,
△ABC中,由余弦定理得AC2=AB2+BC2-2AB•BC•cos∠ABC=4+1-2×2×1×(-)=7,
∴AC=,∴MQ=,MP==;
在△PMN中,由余弦定理得cos∠MNP===-;
又异面直线所成角的范围是(0,],∴AB1与BC1所成角的余弦值为.
故选C.
15.【答案】
【解析】【分析】
本题考查球的体积以及圆柱的体积的求法,考查空间想象能力以及计算能力.
设出球的半径,求出圆柱的体积以及球的体积即可得到结果.
【解答】
解:设球的半径为R,则球的体积为V2=R3,
圆柱的体积为V1=πR2•2R=2πR3,
则==.
故答案为.
16.【答案】
【解析】解:将三棱锥A-DED1选择△ADD1为底面,E为顶点,则VA -DED1=VE -ADD1,
其中S△ADD1=SA1D1DA=,E到底面ADD1的距离等于棱长1,
故.
故答案为:
将三棱锥A-DED1选择△ADD1为底面,E为顶点,进行等体积转化VA -DED1=VE -ADD1后体积易求
本题考查了三棱柱体积的计算,等体积转化法是常常需要优先考虑的策略.
17.【答案】
【解析】【分析】
此题考查点到面的距离,考查线面垂直的判断,及三棱锥的体积公式,属于中档题.
关键是利用体积相等列方程.
【解答】
解:三棱锥A-BCD中,AD,BD,CD两两垂直,
则,
点A到平面BDC的距离为AD=1,
E为AC的中点,
则点E到平面DFC的距离为,
又,,
,,
由余弦定理可得,在中,有
所以,
设点C到平面DEF的距离为d,
又,
,
所以.
故答案为.
18.【答案】①
【解析】【分析】
空间四边形OEC1D1在正方体左右面上的投影是③选项的图形,空间四边形OEC1D1在正方体上下面上的投影是④选项的图形,空间四边形OEC1D1在正方体前后面上的投影是②选项的图形,得到结论.
本题考查平行投影及平行投影作图法,考查在同一图形在不同投影面上的投影不同,本题是一个基础题.
【解答】
解:空间四边形OEC1D1在正方体左右面上的投影是③选项的图形,
空间四边形OEC1D1在正方体上下面上的投影是④选项的图形,
空间四边形OEC1D1在正方体前后面上的投影是②选项的图形,
只有①选项不可能是投影,
故答案为:①.
19.【答案】解:(1)由三视图知,该三视图对应的几何体为一个底面直径为2,母线长为2的圆锥与一个长宽都为2高为1的长方体组成的组合体.
此几何体的体积为;
(2)此几何体的表面积.
【解析】本题主要考查空间几何体的三视图以及几何体的表面积与体积,考查了学生的空间想象能力,培养了学生分析问题与解决问题的能力.
(1)根据空间几何体的三视图,可知原几何体的形状,利用柱体与圆锥的体积即可求得结果;
(2)利用柱体与圆锥的即可得到结果.
20.【答案】(1)证明:在长方体中,因A1A=CC1,A1A∥CC1,可得A1C1∥AC,
A1C1不在平面ACD1内,AC⊂平面ACD1,
则A1C1∥平面ACD1;……………………………………………(4分)
(2)解:因为CD⊥平面ADD1A1,AD1⊂平面ADD1A1,可得CD⊥AD1,
所以异面直线CD与AD1所成角900; ………………………………………………(8分)
(3)解:由三棱锥D1-ACD的体积为,可得,
∴AA1=1.……………………………………………(12分)
【解析】(1)根据直线与平面平行的判定定理可知只需证A1C1∥AC,即可得A1C1∥平面ACD1;
(2)由CD⊥平面ADD1A1,可得CD⊥AD1,异面直线CD与AD1所成角900;
(3)由三棱锥D1-ACD的体积为,可得,即可得解.
本题考查直线与平面平行的判定,直线与直线所成角的计算,考查学生空间想象能力,逻辑思维能力,是中档题.
21.【答案】解:四边形ABCD绕AD旋转一周所成的
几何体,如右图:
S表面=S圆台下底面+S圆台侧面+S圆锥侧面
=πr22+π(r1+r2)l2+πr1l1
=
=
=.
体积V=V圆台-V圆锥
=[25π++4π]×4-×2π×2×2
=×39π×4-×8π
=.
所求表面积为:,体积为:.
【解析】旋转后的几何体是圆台除去一个倒放的圆锥,根据题目所给数据,求出圆台的侧面积、圆锥的侧面积、圆台的底面积,即可求出几何体的表面积.求出圆台体积减去圆锥体积,即可得到几何体的体积.
本题是基础题,考查旋转体的表面积与体积,转化思想的应用,计算能力的考查,都是为本题设置的障碍,仔细分析旋转体的结构特征,为顺利解题创造依据.
22.【答案】(1)证明:取DG中点M,连接AM,CM,
可得AM∥FG,CM∥BF,
又AM∩CM=M,
∴平面ACM∥平面BFG,
∴AC∥平面BFG;
(2)解:由AB⊥DG,AD⊥DG,且AB∩AD=A,
可得DG⊥平面ABCD,
又AB=DG=2,
∴,
∴.
【解析】(1)取DG中点M,连接AM,CM,得AM∥FG,CM∥BF,由面面平行的判定可得平面ACM∥平面BFG,进一步得到AC∥平面BFG;
(2)由AB⊥DG,AD⊥DG,得DG⊥平面ABCD,由已知结合棱锥体积公式可得三棱锥A-BCG的体积.
本题考查直线与平面平行的判定,考查空间想象能力与思维能力,训练了多面体体积的求法,是中档题.
23.【答案】(1)证明:连接交于点,连接.
因为分别是与的中点,
所以.
又因为在平面内,不在平面内,
所以平面.
(2)解:连接,
由于且,
所以四边形为平行四边形,,
异面直线与所成的角为或其补角.
而为正三角形,
所以异面直线与所成的角为.
【解析】本题主要考查空间中的线面关系的证明及异面直线所成角的求法,考查线面垂直判定定理及平面向量的夹角求异面直线所成角,属于中档题.
(1)连结交于点,连结,再运用线面平行的判定方法化简即可求解;
(2)由题意得,直接运用线线角的判定方法化简即可求解.
相关资料
更多








