【数学】安徽省芜湖市顶峰美术学校2018-2019学年高二上学期第一次月考试题

安徽省芜湖市顶峰美术学校2018-2019学年

高二上学期第一次月考试题

（考试时间：120分钟  试卷满分：150分）

注意事项：

1． 答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．

2． 回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上，写在本试卷上无效．

3． 考试结束后，将本试卷和答题卡一并交回．

一、选择题（共12小题，每小题5分，共60分）

1．下面描述中，不是棱锥的几何结构特征的为(　　)

A．三棱锥有四个面是三角形                 B．棱锥都有两个面是互相平行的多边形

C．棱锥的侧面都是三角形                   D．棱锥的侧棱交于一点

2．有下列三组定义：

①有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱；

②用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台；

③有一个面是多边形，其余各面都是三角形的几何体是棱锥．

其中正确定义的个数为（    ）

A．          B．          C．            D．0

3．将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所得的几何体是由(　　)

A．一个圆台、两个圆锥构成 B．两个圆台、一个圆锥构成

C．两个圆柱、一个圆锥构成 D．一个圆柱、两个圆锥构成

4．如图所示的平面结构，绕中间轴旋转一周，形成的几何体形状为(　　)

A．一个球体                              B．一个球体中间挖去一个圆柱

C．一个圆柱                              D．一个球体中间挖去一个棱柱

5．一个几何体的三视图的形状都相同、大小均相等，那么这个几何体不可以是(　　)

A．球              B．三棱锥            C．正方体            D．圆柱

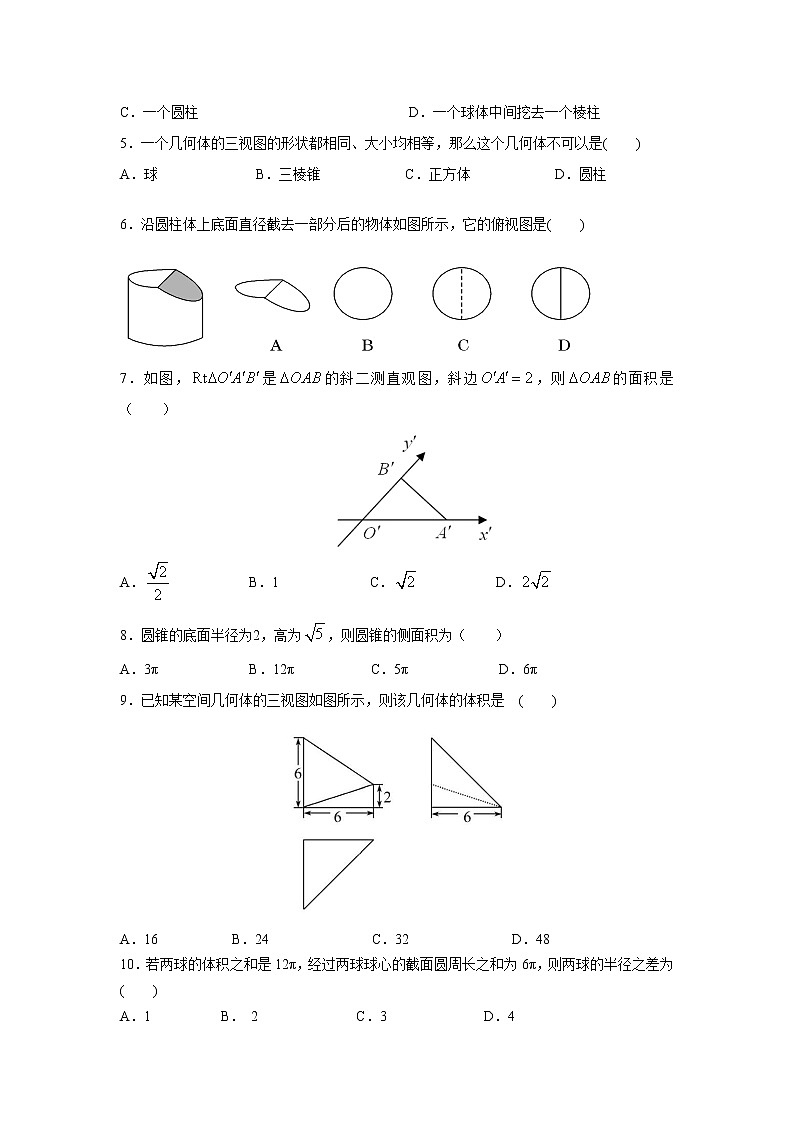
6．沿圆柱体上底面直径截去一部分后的物体如图所示，它的俯视图是(　　)

7．如图，是的斜二测直观图，斜边，则的面积是（    ）

A．           B．1             C．           D．

8．圆锥的底面半径为2，高为，则圆锥的侧面积为（    ）

A．3π             B．12π           C．5π             D．6π

9．已知某空间几何体的三视图如图所示，则该几何体的体积是　(　　)

A．16   B．24    C．32    D．48

10．若两球的体积之和是12π，经过两球球心的截面圆周长之和为6π，则两球的半径之差为(　　)

A．1　        B． 2　　          C．3　　 D．4

11．如果三个球的半径之比是1∶2∶3，那么最大球的表面积是其余两个球的表面积之和的(　　)

A．倍              B．倍               C．2倍           D．3倍

12．已知点在同一个球面上，，若四面体体积的最大值为，则这个球的表面积是（  ）

A．          B．         C．         D．

二、填空题（共4小题，每小题5分，共20分）

13．有下列三个命题：

①圆台的任意两条母线的延长线，可能相交，也可能不相交；②圆锥的母线都交于一点；③圆柱的母线都互相平行．其中正确的命题有____________．

14．如图，矩形O′A′B′C′是水平放置的一个平面图形的直观图，其中O′A′＝6，O′C′＝2，则原图形OABC的面积为_______．

15．一物体及其正视图如图：

则它的侧视图与俯视图分别是图形中的________．

16．已知正三棱柱底面边长为，高为，圆是等边三角形的内切圆，点是圆上任意一点，则三棱锥的外接球的表面积______________．

三、解答题（共6小题，17题10分，18—22题每小题12分，共70分）

17．根据下列对几何体结构特征的描述，说出几何体的名称．

(1)由八个面围成，其中两个面是互相平行且全等的正六边形，其它各面都是矩形；

(2)一个等腰梯形绕着两底边中点的连线所在的直线旋转180°形成的封闭曲面所围成的几何体；

(3)由五个面围成，其中一个面是正方形，其他各面都是有一个公共顶点的全等三角形；

(4)一个圆绕其一条直径所在的直线旋转180°形成的封闭曲面所围成的几何体．

18．如图所示，△ABC在水平面的上方，点在△ABC的上方，画出△ABC在光源下投射到平面内的中心投影．

19．画出如图所示几何体的三视图．

20．一个几何体，它的下面是一个圆柱，上面是一个圆锥，并且圆锥的底面与圆柱的上底面重合，圆柱的底面直径为3 cm，高为4 cm，圆锥的高为3 cm，画出此几何体的直观图．

21．已知长方体，其中，过三点的的平面截去长方体的一个角后，得到如图所示的几何体，这个几何体的体积为，求几何体的表面积．

22．如图，某种水箱用的“浮球”，是由两个半球和一个圆柱筒组成的．已知半球的直径是6 cm，圆柱筒高为2 cm．

(1)这种“浮球”的体积是多少cm3?

(2)要在2 500个这样的“浮球”表面涂一层胶，如果每平方米需要涂胶100克，那么共需胶多少克？

参考答案

1．【答案】B

【解析】根据棱锥的定义可知B错误，棱锥的任何两个面都不平行．

2．【答案】C

【解析】由棱柱的定义可知只有①正确，②中截面必须平行于底面，③中其余各三角形应有一个公共顶点，所以②③都不正确．故选B．

3．【答案】D

【解析】旋转体如图，中间是一个圆柱，两端是相同的圆锥构成，故选D．

4．【答案】B

【解析】外面的圆旋转形成一个球，里面的长方形旋转形成一个圆柱．

5．【答案】D

【解析】球的三视图均为圆，且大小均相等；对于三棱锥O−ABC，当OA，OB，OC两两垂直且OA=OB=OC时，其三视图的形状可以都相同，大小均相等；正方体的三视图是三个大小均相等的正方形；圆柱的三视图中必有一个为圆，其他两个为矩形，故一个几何体的三视图形状都相同，大小均相等，那么这个几何体不可以是圆柱，故选D．

6．【答案】D

【解析】从上面看依然可得到两个半圆的组合图形，注意看得到的棱画实线．

7．【答案】D

【解析】

的面积为．故选D．

8．【答案】D

【解析】圆锥的母线l==3，∴圆锥的侧面积S=πrl=π×2×3=6π，故选D．

9．【答案】D

【解析】由三视图知，该几何体是一个四棱锥E-ABCD，底面ABCD是一个直角梯形，各边长如图所示，BC⊥AB，EB⊥底面ABCD，AB=6，所以由棱锥的体积公式得，

V=××(6+2)×6×6=48．

10．【答案】A

【解析】设两球的半径分别为R、r(R>r)，则由题意得解得故R－r＝1．

11．【答案】B

【解析】设最小球的半径为1，则最大球的表面积S大＝36π，S小＋S中＝20π，．

12．【答案】D

【解析】由可知△ABC为直角三角形，，所以△ABC的外心为的中点，由四面体的体积公式可知，当顶点到平面的距离最大时，有最大体积，当，球心共线时，顶点到平面的距离最大，由题可求得此时顶点到平面的距离为，设球的半径为，则球心到圆心的距离为，则，解得，则球的表面积

，故选D．

13．【答案】②③

【解析】由于圆台是用平行于底面的平面截圆锥得到的，所以其母线必交于一点，故①不正确，②③显然正确．

14．【答案】

【解析】因为矩形是水平放置的一个平面图形的直观图，所以根据画直观图的基本原理知原图形是底边长为6的平行四边形，其高是，因此，原图形OABC的面积是，故答案为．

15．【答案】③②

【解析】侧视图是矩形中间有条实线，应选③；俯视图为矩形中间两条实线，且为上下方向，应选②．

16．【答案】

【解析】由题设可知三棱锥的外接球过上底面的内切圆和下底面的外接圆，容易算得三棱柱的上、下底面的内切圆与外接圆的半径分别为．设球心到上、下底面的距离分别是，则由球心距、球半径及截面圆的半径之间的关系可得

，解得，所以，故球的表面积为

．

17．【解析】(1)该几何体有两个面是互相平行且全等的正六边形，其它各面都是矩形，满足每相邻两个面的公共边都互相平行，故该几何体是正六棱柱，如图(1)．

(2)等腰梯形两底边中点的连线将梯形平分为两个直角梯形，每个直角梯形绕垂直于底边的腰所在直线旋转180°形成半个圆台，故该几何体为圆台，如图(2)．

(3)该几何体的其中一个面是多边形(四边形)，其余各面都是三角形，并且这些三角形有一个公共顶点，符合棱锥的定义，又因为底面是正方形，所以该几何体是正四棱锥，如同(3)．

(4)是一个球，如图(4)．

18．【解析】连接并延长交平面于，连接并延长交平面于，连接并延长交平面于，连接，，，则△为△ABC在下的中心投影，如图所示．

19．【解析】图①为正六棱柱，可按棱柱的画法画出，图②为一个圆锥与一个圆台的组合体，按圆锥、圆台的三视图画出它们的组合形状．三视图如图所示．

20．【解析】画法如下　

(1)画轴．如图1所示，画x轴、z轴，使∠xOz＝90°．

(2)画圆柱的两底面．在x轴上取A、B两点，使AB的长度等于3 cm，且OA＝OB．选择椭圆模板中适当的椭圆过A，B两点，使它为圆柱的下底面．在Oz上截取点O′，使OO′＝4 cm，过O′作Ox的平行线O′x′，类似圆柱下底面的作法作出圆柱的上底面．

(3)画圆锥的顶点．在Oz上截取点P，使PO′等于圆锥的高3 cm．

(4)成图．连接A′A，B′B，PA′，PB′，整理得到此几何体的直观图．如图2所示．

21．【解析】

．

则，设的中点H，

则，表面积．

22．【解析】(1)因为半球的直径是6 cm，所以半径R＝3 cm，

所以两个半球的体积之和为V球＝πR3＝π·27＝36π(cm3)．

又圆柱筒的体积为V圆柱＝πR2·h＝π×9×2＝18π(cm3)．

所以这种“浮球”的体积是V＝V球＋V圆柱＝36π＋18π＝54π(cm3)．

(2)上下两个半球的表面积是S球表＝4πR2＝4×π×9＝36π(cm2)，

又“浮球”的圆柱筒的侧面积为S圆柱侧＝2πRh＝2×π×3×2＝12π(cm2)，

所以1个“浮球”的表面积为S＝＝π(m2)．

因此2500个这样的“浮球”的表面积为2500S＝2500×π＝12π(m2)．

因为每平方米需要涂胶100克，所以共需要胶的质量为100×12π＝1 200π(克)．