初中数学人教版八年级上册第十二章 全等三角形综合与测试精品同步训练题

这是一份初中数学人教版八年级上册第十二章 全等三角形综合与测试精品同步训练题，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题


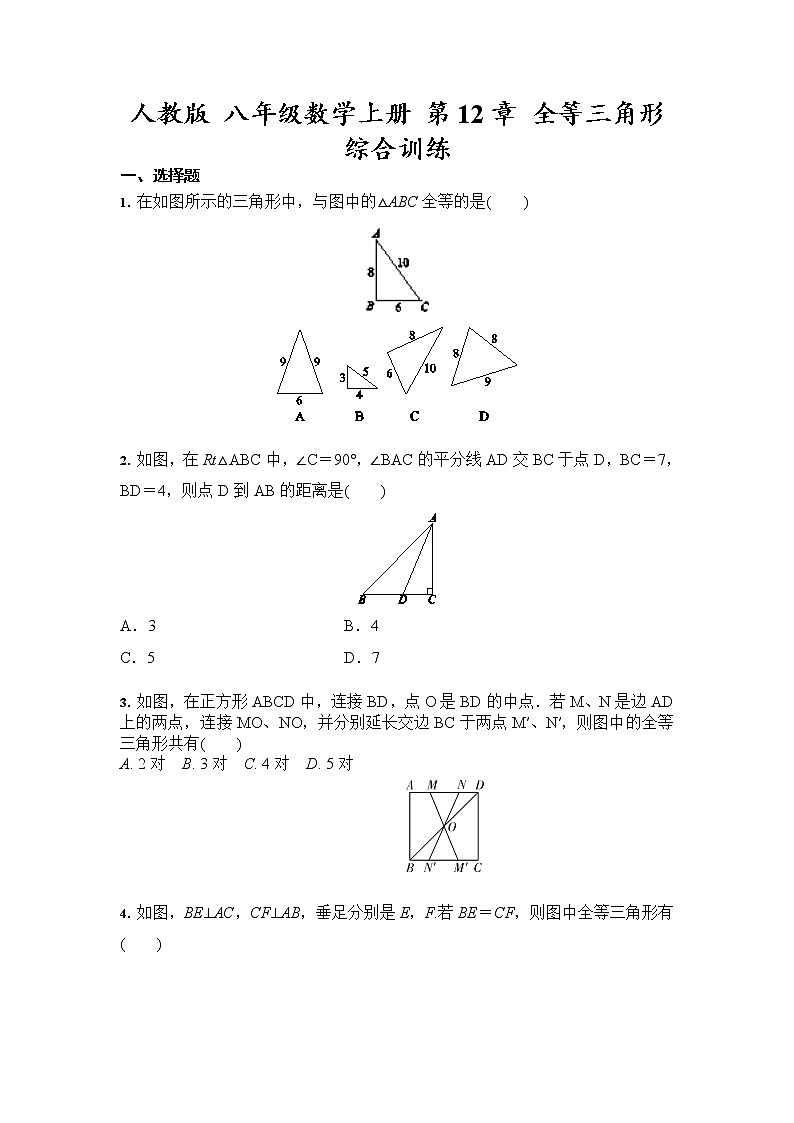
1. 在如图所示的三角形中，与图中的△ABC全等的是( )











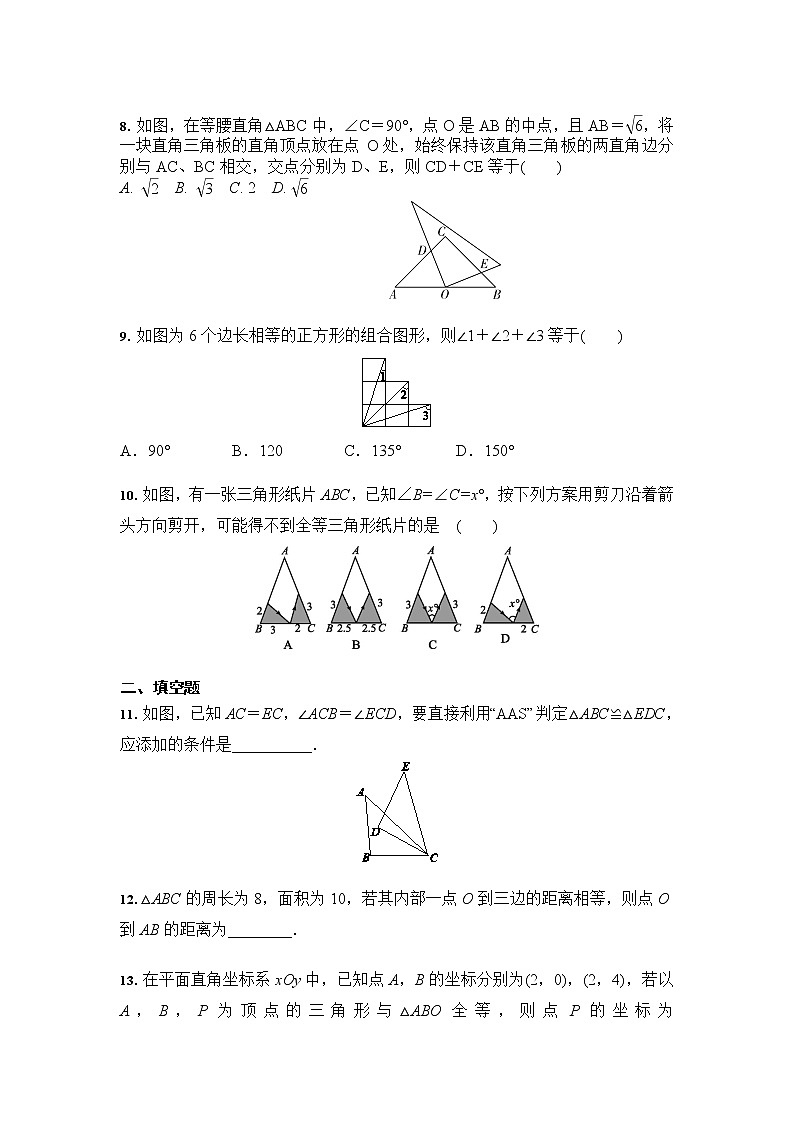
2. 如图，在Rt△ABC中，∠C＝90°，∠BAC的平分线AD交BC于点D，BC＝7，BD＝4，则点D到AB的距离是( )





A．3 B．4


C．5 D．7





3. 如图，在正方形ABCD中，连接BD，点O是BD的中点．若M、N是边AD上的两点，连接MO、NO，并分别延长交边BC于两点M′、N′，则图中的全等三角形共有( )


A. 2对 B. 3对 C. 4对 D. 5对








4. 如图，BE⊥AC，CF⊥AB，垂足分别是E，F.若BE＝CF，则图中全等三角形有( )





A．1对 B．2对 C．3对 D．4对





5. 如图，AB＝AC，AD＝AE，BE＝CD，∠2＝110°，∠BAE＝60°，则下列结论错误的是( )





A．△ABE≌△ACD B．△ABD≌△ACE


C．∠C＝30° D．∠1＝70°





6. 如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE＝DG，△ADG和△AED的面积分别为60和35，则△EDF的面积为( )





A．25 B．5.5 C．7.5 D．12.5





7. 现已知线段a，b(a

小惠:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点A为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求.


小雷:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点O为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求.


则下列说法中正确的是( )


A.小惠的作法正确，小雷的作法错误


B.小雷的作法正确，小惠的作法错误


C.两人的作法都正确


D.两人的作法都错误





8. 如图，在等腰直角△ABC中，∠C＝90°，点O是AB的中点，且AB＝eq \r(6)，将一块直角三角板的直角顶点放在点O处，始终保持该直角三角板的两直角边分别与AC、BC相交，交点分别为D、E，则CD＋CE等于( )


A. eq \r(2) B. eq \r(3) C. 2 D. eq \r(6)








9. 如图为6个边长相等的正方形的组合图形，则∠1＋∠2＋∠3等于( )





A．90° B．120 C．135° D．150°





10. 如图，有一张三角形纸片ABC，已知∠B=∠C=x°，按下列方案用剪刀沿着箭头方向剪开，可能得不到全等三角形纸片的是( )








二、填空题


11. 如图，已知AC＝EC，∠ACB＝∠ECD，要直接利用“AAS”判定△ABC≌△EDC，应添加的条件是__________．








12. △ABC的周长为8，面积为10，若其内部一点O到三边的距离相等，则点O到AB的距离为________．





13. 在平面直角坐标系xOy中，已知点A，B的坐标分别为(2，0)，(2，4)，若以A，B，P为顶点的三角形与△ABO全等，则点P的坐标为________________________．





14. 如图所示，AE=AD，∠B=∠C，BE=4，AD=5，则AC= .








15. 要测量河岸相对两点A，B之间的距离，已知AB垂直于河岸BF，先在BF上取两点C，D，使CD＝CB，再过点D作BF的垂线段DE，使点A，C，E在一条直线上，如图，测出DE＝20米，则AB的长是________米．








16. 如图，在Rt△ABC中，∠ACB＝90°，BC＝2 cm，CD⊥AB，在AC上取一点E，使EC＝BC，过点E作EF⊥AC交CD的延长线于点F.若EF＝5 cm，则AE＝________cm.








17. 如图，P是△ABC外的一点，PD⊥AB交BA的延长线于点D，PE⊥AC于点E，PF⊥BC交BC的延长线于点F，连接PB，PC.若PD＝PE＝PF，∠BAC＝64°，则∠BPC的度数为________．








三、解答题


18. 如图，∠B＝∠D，请添加一个条件(不得添加辅助线)，使得△ABC≌△ADC，并证明．




















19. 如图，已知△ACF≌△DBE，且点A，B，C，D在同一条直线上.若AD=16，BC=10，求AB的长.




















20. 如图，已知△ABC≌△DBE，点D在AC上，BC与DE交于点P，AD＝DC＝2.4，BC＝4.1.


(1)若∠ABE＝150°，∠DBC＝30°，求∠CBE的度数；


(2)求△DCP与△BPE的周长和．




















21. 如图，点E，F在AC上，DF＝BE，AE＝CF，∠AFD＝∠CEB.求证：AD∥CB.




















22. 如图，已知△ABC的周长是20 cm，BO，CO分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD＝4 cm.求△ABC的面积．




















人教版 八年级数学上册 第12章 全等三角形 综合训练-答案


一、选择题


1. 【答案】C





2. 【答案】A





3. 【答案】C 【解析】由题意可知，△ABD≌△CBD，△MON≌△M′ON′，△DON≌△BON′，△DOM≌△BOM′共4对．





4. 【答案】C [解析] ①∵BE⊥AC，CF⊥AB，


∴∠CFB＝∠BEC＝90°.


在Rt△BCF和Rt△CBE中，eq \b\lc\{(\a\vs4\al\c1(CF＝BE，,BC＝CB，))


∴Rt△BCF≌Rt△CBE(HL)．


②∵BE⊥AC，CF⊥AB，∴∠AFC＝∠AEB＝90°.在△ABE和△ACF中，


eq \b\lc\{(\a\vs4\al\c1(∠AEB＝∠AFC，,∠A＝∠A，,BE＝CF，))∴△ABE≌△ACF(AAS)．


③设BE与CF相交于点O.


∵BE⊥AC，CF⊥AB，


∴∠OFB＝∠OEC＝90°.


∵△ABE≌△ACF，∴AB＝AC，AE＝AF.


∴BF＝CE.


在△BOF和△COE中，eq \b\lc\{(\a\vs4\al\c1(∠OFB＝∠OEC，,∠BOF＝∠COE，,BF＝CE，))


∴△BOF≌△COE(AAS)．





5. 【答案】C [解析] ∵BE＝CD，


∴BE－DE＝CD－DE，即BD＝CE.


在△ABD和△ACE中，


eq \b\lc\{(\a\vs4\al\c1(AB＝AC，,BD＝CE，,AD＝AE，))


∴△ABD≌△ACE.


由题意易证：△ABE≌△ACD，故A，B正确．


由△ABE≌△ACD可得∠B＝∠C.


∵∠2＝∠BAE＋∠B，


∴∠B＝∠2－∠BAE＝110°－60°＝50°.


∴∠C＝∠B＝50°.


故C错误．


∵△ABE≌△ACD(已证)，∴∠1＝∠AED＝180°－∠2＝70°.


故D正确．故选C.





6. 【答案】D [解析] 如图，过点D作DH⊥AC于点H.





又∵AD是△ABC的角平分线，DF⊥AB，


∴DF＝DH.


在Rt△ADF和Rt△ADH中，eq \b\lc\{(\a\vs4\al\c1(AD＝AD，,DF＝DH，))


∴Rt△ADF≌Rt△ADH(HL)．


∴SRt△ADF＝SRt△ADH.


在Rt△DEF和Rt△DGH中，eq \b\lc\{(\a\vs4\al\c1(DE＝DG，,DF＝DH，))


∴Rt△DEF≌Rt△DGH(HL)．


∴SRt△DEF＝SRt△DGH.


∵△ADG和△AED的面积分别为60和35，


∴35＋SRt△DEF＝60－SRt△DGH.∴SRt△DEF＝12.5.





7. 【答案】A [解析] AB=b，AB是斜边，小惠作的斜边长是b符合条件，而小雷作的是一条直角边长是b.故小惠的作法正确，小雷的作法错误.





8. 【答案】B 【解析】如解图，连接OC，由已知条件易得∠A＝∠OCE，CO＝AO，∠DOE＝∠COA，∴∠DOE－∠COD＝∠COA－∠COD，即∠AOD＝∠COE，∴△AOD≌△COE(ASA)，∴AD＝CE，进而得CD＋CE＝CD＋AD＝AC＝eq \f(\r(2),2)AB＝eq \r(3)，故选B.








9. 【答案】C [解析] 在图中容易发现全等三角形，将∠3转化为与其相等的对应角后可以看出∠3与∠1互余．故∠1＋∠3＝90°.易得∠2＝45°，故∠1＋∠2＋∠3＝135°.





10. 【答案】C [解析] 选项A中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.


选项B中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.


选项C中，如图①，∵∠DEC=∠B+∠BDE，


∴x°+∠FEC=x°+∠BDE.


∴∠FEC=∠BDE.


这两个角所对的边是BE和CF，而已知条件给的是BD=CF=3，故不能判定两个小三角形全等.


选项D中，如图②，∵∠DEC=∠B+∠BDE，∴x°+∠FEC=x°+∠BDE.


∴∠FEC=∠BDE.


又∵BD=CE=2，∠B=∠C，


∴△BDE≌△CEF.


故能判定两个小三角形全等.








二、填空题


11. 【答案】∠B＝∠D





12. 【答案】2.5 [解析] 设点O到AB，BC，AC的距离均为h，∴S△ABC＝eq \f(1,2)×8·h＝10，解得h＝2.5，即点O到AB的距离为2.5.





13. 【答案】(4，0)或(4，4)或(0，4)





14. 【答案】 9





15. 【答案】20





16. 【答案】3 [解析] ∵∠ACB＝90°，∴∠ECF＋∠BCD＝90°.∵CD⊥AB，∴∠BCD＋∠B＝90°.


∴∠ECF＝∠B.


在△ABC和△FCE中，eq \b\lc\{(\a\vs4\al\c1(∠B＝∠ECF，,BC＝CE，,∠ACB＝∠FEC，))


∴△ABC≌△FCE(ASA)．∴AC＝FE.


∵AE＝AC－CE，BC＝2 cm，EF＝5 cm，


∴AE＝5－2＝3(cm)．





17. 【答案】32° [解析] ∵PD＝PE＝PF，PD⊥AB交BA的延长线于点D，PE⊥AC于点E，PF⊥BC交BC的延长线于点F，


∴CP平分∠ACF，BP平分∠ABC.


∴∠PCF＝eq \f(1,2)∠ACF，∠PBF＝eq \f(1,2)∠ABC.


∴∠BPC＝∠PCF－∠PBF＝eq \f(1,2)(∠ACF－∠ABC)＝eq \f(1,2)∠BAC＝32°.





三、解答题


18. 【答案】


解：答案不唯一，如：添加∠BAC＝∠DAC.


证明：在△ABC和△ADC中，


eq \b\lc\{(\a\vs4\al\c1(∠B＝∠D，,∠BAC＝∠DAC，,AC＝AC，))


∴△ABC≌△ADC(AAS)．





19. 【答案】


解:∵△ACF≌△DBE，∴AC=DB.


∴AC-BC=DB-BC，即AB=CD.


∵AD=16，BC=10，


∴AB=CD=(AD-BC)=3.





20. 【答案】


解：(1)∵∠ABE＝150°，∠DBC＝30°，


∴∠ABD＋∠CBE＝120°.


∵△ABC≌△DBE，∴∠ABC＝∠DBE.


∵∠ABD＝∠ABC－∠DBC，∠CBE＝∠DBE－∠DBC，


∴∠ABD＝∠CBE＝60°，


即∠CBE的度数为60°.


(2)∵△ABC≌△DBE，


∴DE＝AC＝AD＋DC＝4.8，BE＝BC＝4.1.


∴△DCP与△BPE的周长和＝DC＋DP＋BP＋CP＋PE＋BE＝DC＋DE＋BC＋BE＝15.4.





21. 【答案】


证明：∵AE＝CF，


∴AE－EF＝CF－EF，即AF＝CE.


在△ADF和△CBE中，eq \b\lc\{(\a\vs4\al\c1(DF＝BE，,∠AFD＝∠CEB，,AF＝CE，))


∴△ADF≌△CBE(SAS)．


∴∠A＝∠C.∴AD∥CB.





22. 【答案】


解：∵BO，CO分别平分∠ABC和∠ACB，


∴点O到AB，AC，BC的距离相等．


∵△ABC的周长是20 cm，OD⊥BC于点D，且OD＝4 cm，∴S△ABC＝eq \f(1,2)×20×4＝40(cm2)．