初中数学沪科版九年级上册21.2 二次函数的图象和性质优质课第三课时教案设计

这是一份初中数学沪科版九年级上册21.2 二次函数的图象和性质优质课第三课时教案设计，共6页。教案主要包含了知识目标，能力目标，情感态度目标等内容，欢迎下载使用。



















课题
3课时y＝ax+h2
单元
学科
年级
学习


目标
一、知识目标


1.使学生能利用描点法画出二次函数y＝ax+h2的图象。


2．让学生经历二次函数y＝ax+h2性质探究的过程，理解函数y＝ax+h2的性质，解二次函数y＝ax+h2的图象与二次函数y＝ax2的图象的关系。


二、能力目标


1．通过学生自己的探索活动，对二次函数性质的研究，达到对抛物线自身特点的认识和对二次函数性质的理解．


2．经历探索二次函数的图象的作法和性质的过程，培养学生的探索能力．


三、情感态度目标


1．经历观察、猜想、总结等数学活动过程，发展合情推理能力和初步的演绎推理能力，能有条理地、清晰地阐述自己的观点．


2．让学生学会与人合作，并能与他人交流思维的过程和结果．
重点
会用描点法画出二次函数y=ax+h2的图象，理解二次函数y＝ax+h2的性质，理解二次函数y＝ax+h2的图象与二次函数y＝ax2的图象的关系是教学的重点
难点
理解二次函数ax+h2的图象与二次函数y＝ax2的图象的相互关系是教学的难点。
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
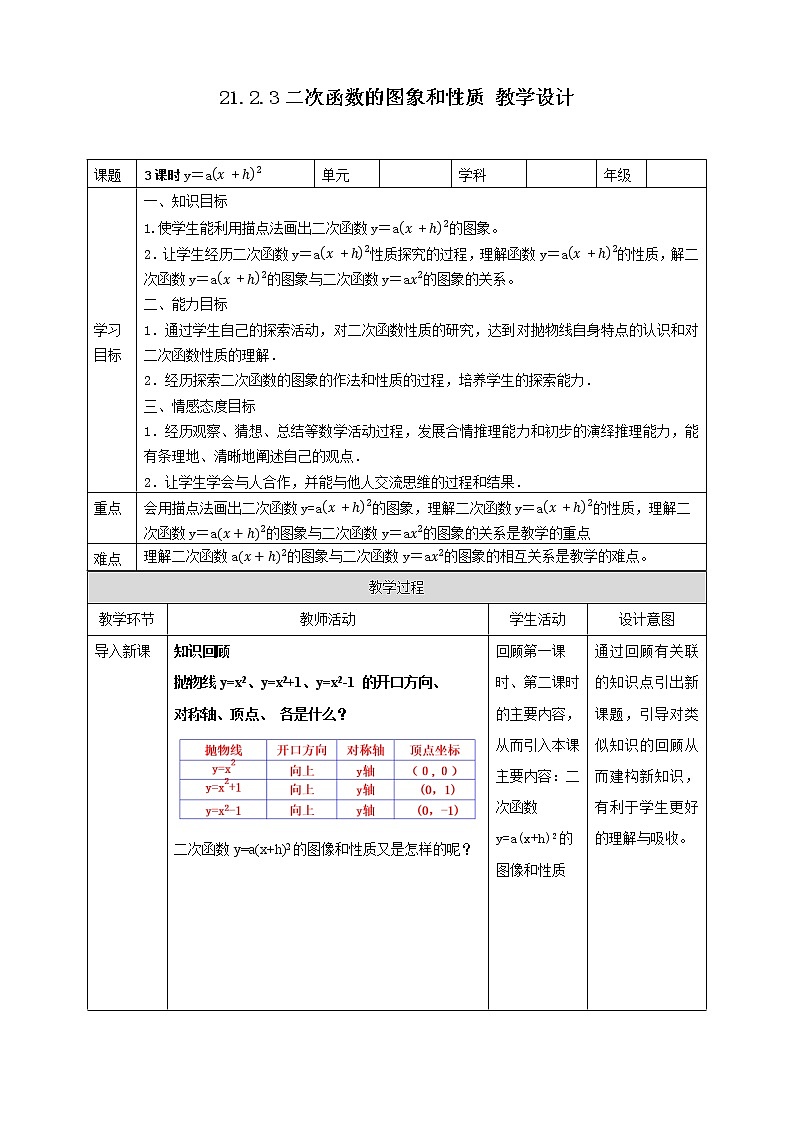
知识回顾


抛物线y=x2、y=x2+1、y=x2-1 的开口方向、


对称轴、顶点、 各是什么？





二次函数y=a(x+h)2的图像和性质又是怎样的呢？
回顾第一课时、第二课时的主要内容，从而引入本课主要内容：二次函数y=a(x+h)2的图像和性质












通过回顾有关联的知识点引出新课题，引导对类似知识的回顾从而建构新知识，有利于学生更好的理解与吸收。
讲授新课
探究新知


1、在同一直角坐标系中，画出函数


和，


的图象，并分别指出他们的开口方向、对称轴和顶点.





列表、描点、连线











归纳：


可以看出，抛物线y=-12(x+1)2的开口向下，对称轴是经过点（－1，0）且与x轴垂直的直线，我们把它记作直线x=－1，顶点是（－1，0）；抛物线 的开口向 下 ，对称轴是直线x = 1，顶点是( 1 , 0 )．





2、在坐标系中画出下列各函数图象并根据函数图象完成表格，说一说抛物线 y = a ( x+h)2 的特点








归纳：


抛物线 y = a ( x+h)2 的特点：


a＞0时，开口____向上__, 最 __低__ 点是顶点;


a＜0时，开口___向下__, 最 _高_ 点是顶点;


对称轴是 _直线 x = -h__，顶点坐标是 ( -h,0 )





3、二次函数 y=a(x+h)²图象的平移


抛物线 y=-12(x+1)2, 与抛物线 有什么关系？





可以发现，把抛物线 向左平移1个单位，就得到抛物线


把抛物线 向右平移1个单位，就得到抛物线 ．





归纳：


二次函数y=a(x+h)2的图象的平移:





y=a(x+h)2与y=ax2 的形状、开口大小和开口方向相同.抛物线y=a(x+h)2 可由抛物线y=ax2沿x轴方向平移︱h︱个单位得到，当h＞0时，向左平移；当h＜0时，向右平移.



学生自己动手操作，根据函数解析式画出对应的函数图像，并讨论分析们的开口方向、对称轴和顶点.。
































学生根据讨论分析结果，自主总结归纳二次函数y=(x+h)2的图像性质，从而解决本课第一个重点。

















运营表格形式多维度总结二次函数


y=a(x+h)2的性质，同时也应用了新知，达到活学活用、举一反三。








由学生画出抛物线， y=-12x2


的图像并与


y=-12(x+1)2


和 y=-12(x-1)2


的图像作对比，思考3条抛物线是什么关系？将其中一条怎么平移能得到另外一条或两条？








根据画出的图像讨论函数之间的关系，归纳总结二次函数y=a(x+h)2的图象的平移规律。
通过列表、描点、连线等画图操作，锻炼学生的画图技能，并通过讨论分析图像的特点。


























渗透数形结合的数学思想，总结二次函数y=a(x+h)2的性质。真正的把课堂还给学生，体现了学生是主体，自主探究的教学设计。


同时也加强了学生自主学习能力、总结归纳能力、迁移运用能力等学科能力。


























进一步引导学生思考第一课时学习的函数图像与本课学习的函数图片有何联系，从而引发学生深层思考，并对本节第二个重点进行探究。









































通过归纳总结，进一步理解二次函数y=a(x+h)2的图象与其他函数的关联，学生自己得出结论加深了理解层次与学习效果。
课堂练习：


1.二次函数 的最小值是（ ）


A.-1 B.1 C.0 D.没有最小值





2.抛物线 不经过的象限是（ ）


A.第一、二象限 B.第二、四象限


C.第三、四象限 D.第二、三象限





3.（1）抛物线 向_左_平移__1__个单位得抛物线


(2)抛物线_ y=2x2__向右平移2个单位得抛物线 .



通过随堂练习题，巩固学生本课所学的同时，检测学生对新知的吸收应用效果，帮助教师掌握本课教学目标是否达成。
课堂小结
抛物线y＝a(x+h)2的性质:


（1）对称轴是直线x＝__ -h__;


（2）顶点坐标是__ (-h,0)___.


(3)当a>0时，开口向上，在对称轴的左侧y随x的增大而_减小_；在对称轴的右侧y随x的增大而_增大__.


（4）当a<0时，开口向下，在对称轴的左侧y随x的增大而_增大_;在对称轴的右侧y随x的增大而_减小.



课堂小结用列表的形式，把本节课所归纳的结论在表格中类比展现，便于学生记忆
拓展延伸



共享单车为市民出行带来了方便，某单车公司第一个月投放a辆单车，计划第三个月投放单车y辆，设该公司第二、三两个月投放单车数量的月平均增长率为x，那么y与x的函数关系是？.



巩固知识，让学生开拓思维。通过解决实际应用问题，达到巩固新知、学以致用的目的，帮助学生进一步提升知识的应用能力。
中考连接
（淄博·2018）已知：抛物线


（1）写出抛物线的对称轴；


（2）完成下表；





（3）在下面的坐标系中描点画出抛物线的图象





解答：


解：（1）抛物线的对称轴为直线x=-1


（2）填表如下：


x
…
-7
-5
-3
-1
1
3
5
…

y
…
-9
-4
-1
0
-1
-4
-9
…

（3）描点作图如下



把新知链接中考真题，通过每节课的真题练习，提高学生对中考题目的解答能力。
板书