九年级上册第21章 二次函数与反比例函数21.2 二次函数的图象和性质一等奖教案

这是一份九年级上册第21章 二次函数与反比例函数21.2 二次函数的图象和性质一等奖教案，共9页。教案主要包含了教学目标等内容，欢迎下载使用。
















课题
21.2.1二次函数的图象和性质
单元
21章
学科
数学
年级
九
学习


目标
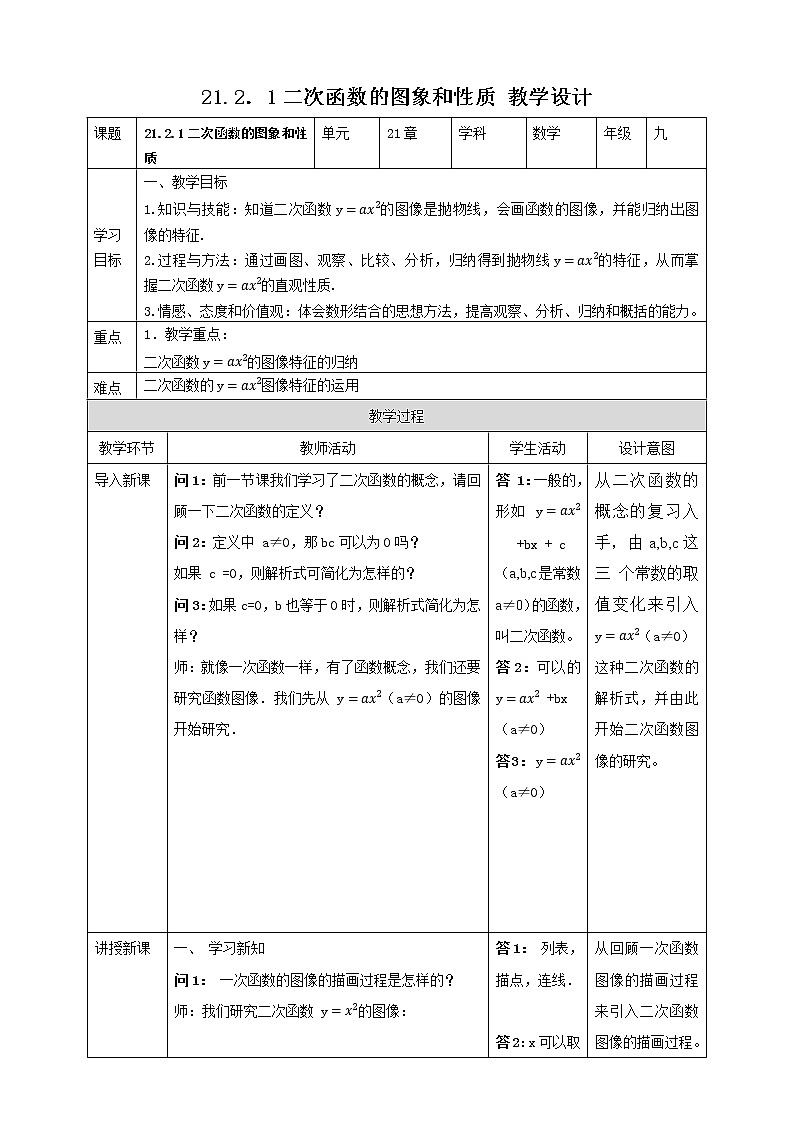
一、教学目标


1.知识与技能：知道二次函数y=ax2的图像是抛物线，会画函数的图像，并能归纳出图 像的特征.


2.过程与方法：通过画图、观察、比较、分析，归纳得到抛物线y=ax2的特征，从而掌 握二次函数y=ax2的直观性质.


3.情感、态度和价值观：体会数形结合的思想方法，提高观察、分析、归纳和概括的能力。
重点
1．教学重点：


二次函数y=ax2的图像特征的归纳
难点
二次函数的y=ax2图像特征的运用
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
问1：前一节课我们学习了二次函数的概念，请回顾一下二次函数的定义？


问2：定义中 a≠0，那bc可以为0吗？


如果 c =0，则解析式可简化为怎样的？


问3：如果c=0，b也等于0时，则解析式简化为怎样？


师：就像一次函数一样，有了函数概念，我们还要研究函数图像．我们先从 y=ax2（a≠0）的图像开始研究．






答 1：一般的，形如 y=ax2+bx+c


（a,b,c是常数a≠0）的函数，叫二次函数。


答2：可以的 y=ax2+bx（a≠0）


答3： y=ax2


（a≠0）












从二次函数的概念的复习入 手，由a,b,c这三 个常数的取值变化来引入 y=ax2（a≠0）


这种二次函数的解析式，并由此 开始二次函数图像的研究。



讲授新课
学习新知


问1： 一次函数的图像的描画过程是怎样的？


师：我们研究二次函数 y=x2的图像：





问2：先列表，首先要考虑自变量的取值范围，自变量x的取值范围是什么？


师：考虑自变量x可以取任意实数，因此以0为中心选取x的值，列出函数对应值表.





师：然后在几何画板的坐标平面中描点，在描点过程中分别取x的值和相应的函数值y作为点的坐标





师：最后用平滑的曲线顺次联结各点，得到函数 y=x2的图像





师：二次函数 y=x2的图像是一条曲线，它属于一类特殊的曲线。


这类曲线称为抛物线．二次函数 y=x2的图像就称为抛物线 y=x2。





问1：图形与y轴的交点在哪里？


问2：图形从直观上有何特点？是否对称？开口方向如何？


师：我们来探讨一下图形为何是一个轴对称图形： 问3：刚才取点时取得x的点除0外都是互为相反数，这些互为相反数的x的值所对应y的值有何特点？


问4：互为相反的x的值和对应的y的值在直角坐标系中所表示的点有何特点？


问5：满足与y轴对称的点的集合是一个曲线，那么这样的曲线有何特征呢？


问6：对称轴两侧的对称点的连线段和y轴之间有着怎样的关系？


问7：此图形有无最高点、最低点，为什么？


师：我们发现，这个最低点是图像与对称轴的交点，即是原点O．除这个交点外，抛物线上所有的点都在x轴的上方，因而这个交点是抛物线的最低点。


抛物线的顶点：抛物线与它的对称轴的交点叫抛物线的顶点． 抛物线 y=x2的顶点是原点O（0，0）。























【适时小结】


抛物线 y=x2的图形特征：


1、开口方向向上；


2、是轴对称图形，对称轴是y轴，即直线x=0；


3、抛物线的顶点是原点O（0，0）





试一试：用上述方法取相同的x的值画出二次函数 y=-x2的图像，与 y=x2的图像进行比较再归纳它的特征.











问1：取与 y=x2相同的x的值，我们发现 y=-x2所得到的y值与 y=x2的y值有何特点？


问2：为何会这样？


问3：这样的话抛物线会有怎样的变化？


问:4： y=x2的图像与 y=-x2的图像之间有没有对称性？


问5： y=x2和 y=-x2在图像上有何异同？先讲讲有何相同之处？








【适时小结】


抛物线 y=-x2的图像特征：


1、 开口方向向下；图像在y轴左侧部分 上升，y轴右侧部分下降．


2、 它是轴对称图形，对称轴是y轴，即 直线x=0. 3、 顶点是坐标原点，而且它是抛物线的最高点． y=-x2的图像与 y=x2的图像关于x轴对称．








































































































例题 在同一个平面直角坐标系xOy中，分别画出二次函数y=12x2 和 y=2x2


和的图像．


问1：画图像时如何取点，怎么取？


（1）列表：





⑵描点：（教师描点，连线）





问2：连线时要注意什么？


⑶连线：


问3:抛物线y=12x2 和 y=2x2


和有何共同特征？





问4：有何不同？





问5:从 y=x2的图像与 y=-x2的图像开口方向和比较；以及 和开口方向的比较，我们是否可以得出) y=ax2（a≠0）当a大于或小于零时，开口方向的变化规律？





【适时小结】


一般，二次函数 y=ax2（a≠0）图像 是抛物线，称为抛物线 y=ax2（a≠0）


2、 抛物线 y=ax2（a≠0）是轴对称图 形，对称轴是y轴,即直线x=0;


3、 顶点坐标是原点，抛物线的开口方向由a所取值的符号决定，当a>0时，它开口向上，顶点是抛物线的最低点；当a<0时，它开口向下，顶点是抛物线的最高点





师：把 y=x2的图像与 y=-x2 和 显示在同一个几何画板，进行比较。





问：从上图的 y=ax2


（a≠0）的图像中， 我们猜测一下，|a|的大小与抛物线开口大 小有没有关系？
答1： 列表，描点，连线．





答2：x可以取一切实数．


教师取x值，由学生回答y值共同完成数值列表。








































































































答1：在坐标原点


答2：轴对称;开口方向向上．


答3：每一对互为相反的x的值所对应的y的值都相等．


答4：都关于y轴对称．


答5：曲线关于y轴对称


答6：对称轴垂直平分对称点的连接线段．


答7：此图形在y轴两边分别向左上方和右上方无限伸展，因而没有最高点，只有最低点，为坐标原点。

































































答1：相同x的值所对应的y值互为相反


数．


答2：因为 y=x2与y=-x2的解析式的比较中，明显是x2前的系数由+1变成-1.函数值是互为相反数的关系．


答3：所以从图像看曲线开口由向上变成了向下．


答4：两个图像关于x轴对称


答5： 相同点：


1） 都是抛物线，且抛物线的顶点是同一个点，都是坐标原点。


2） 都关于y轴（直线x=0）对称．


不同点：


1）抛物线 y=x2开口方向向上， 图像在y轴左侧部分下降，y轴右侧部分上升．抛物线 y=-x2开口 方向向下，图像在y轴左侧部分是上升的，右侧部分是下降的．


2） y=x2顶点是图像最低y=-x2顶点是图像最高点











学生回答，教师补充．


答1：列表，选取原点及两侧各3个对称点共7个点，列表取x值，计算y值。
































答2：连线时要用光滑的曲线联结，注意两边要出头．








答3： 都是以y轴为对称轴的轴对称图形，顶点都是原点


答4：抛物线 开口向上， 向左上方和右上方无限延伸，在y轴左侧部分下降，在y轴右侧部分上升．


顶点是抛物线最低点．


抛物线 开口向下，向左 下方右下方无限延伸，在y轴左侧部分上升，在y轴右侧部分下降．顶点是抛物线最高点。





答5：当a>0时，开口方向向上；a<0时，开口方向向下。



































答：有，|a|越大，抛物线开口就 越小；反之，|a|越小，抛物线开 口就越大
从回顾一次函数图像的描画过程来引入二次函数图像的描画过程。




















这里可以告诉学生；既然x可以取一切实数（正数，负数和零），我们不妨选取零和一些互为相反的正负数． 数值表的取值中，x值由老师提出，可由学生算出y值．


教师在几何画板中输入坐标数对，几何画板自动生成平面上的点．这样比黑板画图更为漂亮、精确和高效，也便于下一步连线成抛物线。


在几何画板中用函数绘制工 具画出 y=x2的图像，曲线经过已取的各点．表明这些点的几何即为此抛物线。





此时引出抛物线的概念，便于后面反复提及和强调此概念。








通过这一系列的问题，我们引出了图像的一系列的特征：轴对称；开口方向向上；无限延伸特性；抛物线顶点概念以及图像的最低点特征。

















































































































通过比较图像的异同点，强化此类二次函数图像的特征。















































































































































学生取值，直接把两个函数放在．便于比较数据与图像之间关于这两个函数的比较





















课堂练习：


1.在同一平面直角坐标系中画出y=13x2 、y=-13x2 、y=3x2 和y=-3x2的图像。








2.抛物线y=13x2与抛物线y=-13x2的图像有何共同点和不同点？两条抛物 线有怎样的对称性？





答1： 共同点：它们都是以y轴为对称轴的轴对称图形，顶点都是原点．不同点：抛物线y=13x2开口向上， 向左上方和右上方无限延伸，在y轴左侧部分下降，在y轴右侧部分上升．顶点是抛物线最低点． 抛物线y=-13x2开口向下，向左下方右下方无限延伸，在y轴左侧部分上升，在y轴右侧部分下降．顶点是抛物线最高点。





3.已知关于x的二次函数y=1+2kx2当k为何值时，它的图像开口向上？当k为何值时，它的图像开口向下。


答2：K> 12 ,开口向上，K<-12 开口向下


4.已知y=-3x2、②y=32x2、③ y=-253x2，把这三个二次函数图像开口大小由小到大按序号排列


答3:②、①、③



课堂练习中增加了|a|的大小与抛物线开口大小之间的关系的习题．
课堂小结
课堂小结：



课堂小结用列表的形式，把本节课所归纳的结论在表格中类比展现，便于学生记忆
板书