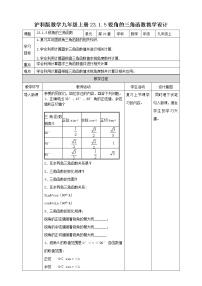
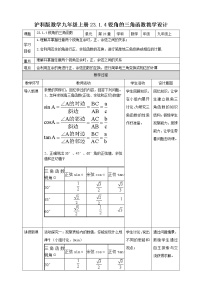
- 23.1.1 锐角的三角函数 第1课时 教案 教案 13 次下载
- 23.1.2 锐角的三角函数 第2课时 教案 教案 12 次下载
- 23.1.4 锐角的三角函数 第4课时 教案 教案 11 次下载
- 23.1.5 锐角的三角函数 第5课时 教案 教案 11 次下载
- 23.2.1 解直角三角形及其应用 第1课时 教案 教案 11 次下载
初中数学23.1 锐角的三角函数一等奖第3课时教案
展开课题
23.1.3 锐角的三角函数
单元
第23章
学科
数学
年级
九年级上
学习
目标
1、运用三角函数的概念,自主探究求出角的三角函数值
2、熟记三个特殊角的三角函数值,并能准确的加以运用,即给出特殊角能说出它的三角函数值,反过来,给出特殊角的数值,能说出相应的锐角的度数。
重点
三个特殊角的三角函数值极其运用
难点
特殊角三角函数值的应用
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
亲爱的同学们,回忆之前学过的内容,回答下列问题。
1、锐角三角函数的定义 (正弦、余弦和正切)的定义是什么?
正弦的定义:在Rt△ABC中,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine)
记作: sinA
余弦的定义:在Rt△ABC中,我们把锐角A的邻边与斜边的比叫做∠A的余弦(csine)
记作:csA
正切的定义:在Rt△ABC中,如果锐角A确定,那么,∠A的对边与邻边的比值总是一个固定值。这个比叫做∠A的正切(tangent)。 记作: tanA
对于锐角A的每一个确定的值,tanA都有唯一的确定的值与它对应.
2、在直角三角形中,30°的角有什么性质呢?
在直角三角形中, 30°的角所对的直角边等于斜边的一半。
由学生独立思考,并口答得出定义正弦、余弦和正切的定义,总结出锐角三角函数的定义.
“温故知新”是传统的教学手段,为应用作准备.自然、合理,符合学生的任知规律。
讲授新课
活动探究:阅读课本内容,思考下列问题
如图(1),在在Rt△ABC 中, ∠C= 90°, ∠A= 30º , ∠B= 60º
1、设BC=1,则AB和AC的长各是多少?为什么?
2、求下列各式的值。
1)sin300 =_____, cs300 =_____, tan300 =_____
2)sin600 =_____,cs600 =_____ , tan600 =_____
如图(2),在Rt△ABC 中, ∠C= 90°, ∠A= ∠B= 45º
1、设BC=1,则AB和AC的长各是多少?为什么?
2、sin450 =_____, cs450 =_____, tan450 =_____
特殊角的三角函数值表
三角函数锐角α
正弦sinα
余弦csα
正切tanα
30°
45°
60°
口诀记忆30°、45°、60°三角函数值
一、二、三,三、二、一,根三分之一,一根三.
例4 、求下列各式的值:
(1)2sin60°+ 3tan300+tan45°;
(2) cs245°+ tan60°cs 30°.
注意:cs245°表示(cs45°)2,类似地
sin2A°表示(sinA)2, tan2A°表示(tanA)2.
1、填空:
若 ,则 α=_______;
若 ,则α=________;
若 ,则α=_________.
2、求下列各式的值:
(1)sin60°-cs45°
(2)cs60°+tan60°
中考链接
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.那么,怎样求旗杆的高度呢?
让学生思考讨论,教师巡回检查.对个别学生稍加点拨,最后请学生回答。
让学生通过观察、归纳、总结出正弦和余弦的定义.
背诵三角函数值,并当堂提问。
通过例题的学习进一步探究,由易到难,加深对知识点的理解和掌握.
学生要独立完成练习,然后进行展示,其他学生相互补充。
链接中考,层层深入。拓展学生的思维,加强学生应对难题的能力。
通过问题情景,鼓励学生通过自主探索与交流获得求解。通过学习,培养学生分析问题、寻找最佳解题途径的能力.
引导学生再次思考。
学法小结,着重强调分析方法,养成归纳小结的良好习惯。
作业
必做题:
1、随堂练习 P72
2、填一填教材118页练习第1题的特殊角的函数表。
选做题:习题 P118第2、3题。
作业要求学生独立完成
养成独立完成作业的习惯
课堂小结
三角函数锐角α
正弦sinα
余弦csα
正切tanα
30°
45°
60°
引导学生自己小结
鼓励学生畅所欲言,总结对本节课的收获和体会;自主建构知识体系,锻炼学生的口头表达能力,培养学生的自信心;进一步加深对所学知识的理解和记忆
板书
23.1.3 锐角的三角函数
1、特殊角的三角函数值
2、特殊角的三角函数值的应用
初中数学沪科版九年级上册23.1 锐角的三角函数教案设计: 这是一份初中数学沪科版九年级上册23.1 锐角的三角函数教案设计,共2页。教案主要包含了课堂练习,学习小结等内容,欢迎下载使用。
初中沪科版23.1 锐角的三角函数教案设计: 这是一份初中沪科版23.1 锐角的三角函数教案设计,共2页。教案主要包含了情境导入,合作探究,板书设计等内容,欢迎下载使用。
2021学年23.1 锐角的三角函数第2课时教学设计及反思: 这是一份2021学年23.1 锐角的三角函数第2课时教学设计及反思,共3页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点,教学难点,教学说明,归纳结论等内容,欢迎下载使用。