沪科版九年级上册23.1 锐角的三角函数优秀第4课时教学设计

这是一份沪科版九年级上册23.1 锐角的三角函数优秀第4课时教学设计，共4页。
















课题
23.1.4锐角的三角函数
单元
第23章
学科
数学
年级
九年级上
学习


目标
1.理解并掌握任意两个锐角互余时，正、余弦之间的关系；


2.会利用互余的角进行正、余弦函数的互换，进行简单地三角变换或相应的计算.
重点
理解并掌握任意两个锐角互余时，正、余弦之间的关系
难点
会利用互余的角进行正、余弦函数的互换，进行简单地三角变换或相应的计算
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
亲爱的同学们，回忆学过的内容，回答下列问题。


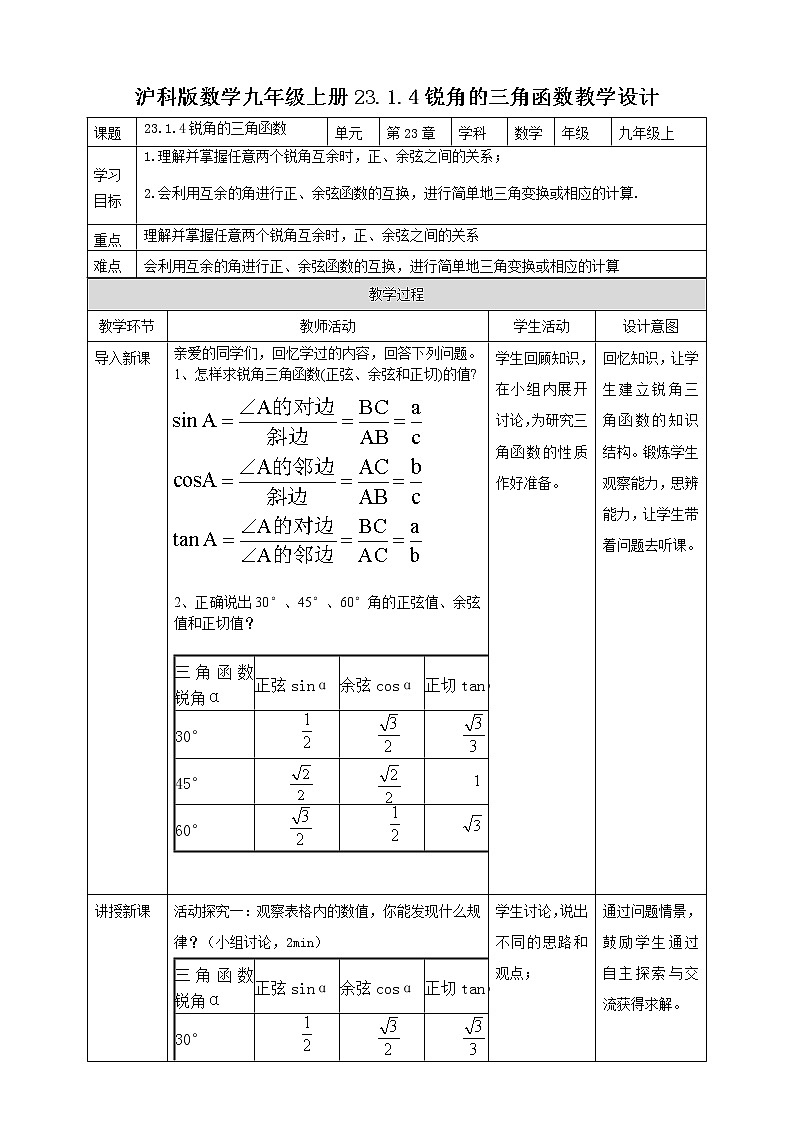
1、怎样求锐角三角函数(正弦、余弦和正切)的值?
































2、正确说出30°、45°、60°角的正弦值、余弦值和正切值？





三角函数锐角α
正弦sinα
余弦csα
正切tanα

30°




45°




60°








学生回顾知识，在小组内展开讨论，为研究三角函数的性质作好准备。
回忆知识，让学生建立锐角三角函数的知识结构。锻炼学生观察能力，思辨能力，让学生带着问题去听课。



讲授新课
活动探究一：观察表格内的数值，你能发现什么规律？（小组讨论，2min）


三角函数锐角α
正弦sinα
余弦csα
正切tanα

30°




45°




60°




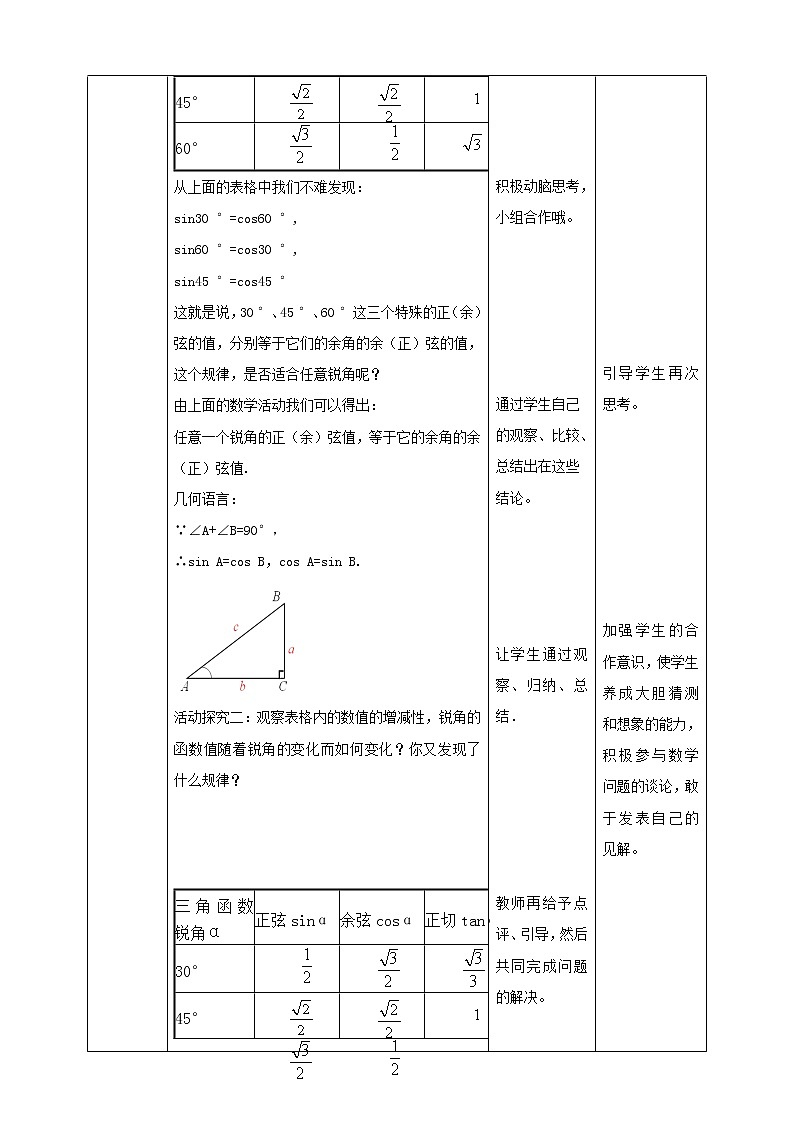
从上面的表格中我们不难发现：


sin30 °=cs60 °,


sin60 °=cs30 °,


sin45 °=cs45 °


这就是说，30 °、45 °、60 °这三个特殊的正（余）弦的值，分别等于它们的余角的余（正）弦的值，这个规律，是否适合任意锐角呢？


由上面的数学活动我们可以得出：


任意一个锐角的正（余）弦值，等于它的余角的余（正）弦值.


几何语言：


∵∠A+∠B=90°，


∴sin A=cs B，cs A=sin B.





活动探究二：观察表格内的数值的增减性，锐角的函数值随着锐角的变化而如何变化？你又发现了什么规律？











三角函数锐角α
正弦sinα
余弦csα
正切tanα

30°




45°




60°




活动探究三：观察表格内的数值，锐角A的正弦值、余弦值和正切值有无变化范围？


1.互余两角三角函数关系:


SinA=cs（900-A）


csA=sin（900-A）


2、三角函数的变化规律：


锐角的正弦值随着锐角的增大而_______，


锐角的余弦值随着锐角的增大而_______，


锐角的正切值随着锐角的增大而_______


3、锐角α的取值范围是0°＜α＜ 90° 各函数值的取值范围：


正弦 0＜ sinα＜1


余弦 0＜ csα＜1


正切 tanα>0


例5、 在Rt△ABC中，∠C＝90°，且sinA＝ ，求csB的值。




















中考链接：


已知cs α＝ ，α＋β＝90°，则cs β＝( )
学生讨论，说出不同的思路和观点；

















积极动脑思考，小组合作哦。

















通过学生自己的观察、比较、总结出在这些结论。














让学生通过观察、归纳、总结．

















教师再给予点评、引导，然后共同完成问题的解决。











学生要独立完成练习，然后进行展示，其他学生相互补充。




















学生通过练习检验自己对本节知识的掌握情况．











链接中考，层层深入。






通过问题情景，鼓励学生通过自主探索与交流获得求解。
































引导学生再次思考。




















加强学生的合作意识，使学生养成大胆猜测和想象的能力，积极参与数学问题的谈论，敢于发表自己的见解。






































梳理知识点，理解三角函数的性

















课堂深化拓展练习，将比较难的问题、中考考题、放在适当的时候处理，使学生易于接受，提高思维。












作业
必做题:


随堂练习 P73


选做题:习题 P119第1、2和3题
作业要求学生独立完成
养成独立完成作业的习惯



课堂小结
1.互余两角三角函数关系:


SinA=cs（900-A）


csA=sin（900-A）


2、三角函数的变化规律：


锐角的正弦值随着锐角的增大而_______，


锐角的余弦值随着锐角的增大而_______，


锐角的正切值随着锐角的增大而_______


3、锐角α的取值范围是0°＜α＜ 90° 各函数值的取值范围：


正弦 0＜ sinα＜1


余弦 0＜ csα＜1


正切 tanα>0



学生回顾本课时知识技能和思想方法。参与全班交流。






让学生通过知识性内容的小结，提高归纳的能力。






板书



23.1.4 锐角的三角函数





1、互余两角三角函数关系





2、 三角函数的变化规律