初中数学沪科版九年级上册第23章 解直角三角形23.2解直角三角形及其应用获奖课件ppt

这是一份初中数学沪科版九年级上册第23章 解直角三角形23.2解直角三角形及其应用获奖课件ppt，共20页。PPT课件主要包含了新知导入，°6’，课堂练习，解根据勾股定理得，已知斜边求直边，已知直边求直边，已知两边求一边，已知两边求一角，已知直边求斜边，计算方法要选择等内容，欢迎下载使用。
1、亲爱的同学们，我们已经学过直角三角形的性质，那么直角三角形三条边有什么关系？2、锐角之间有什么关系呢？3、边角之间有什么关系呢？
(1) 三边之间的关系: a2+b2=_____；
(2)锐角之间的关系：∠A+∠B=_____；
(3)边角之间的关系：sinA=_____， csA=_____， tanA=_____。
如图，在Rt△ABC中，共有六个元素（三条边，三个角），其中∠C=90°，那么其余五个元素之间有怎样的关系呢？
对于锐角B,也有类似的边角关系吗？
同学们，想一想，有了以上关系，知道五个元素中的几个，就可以求出其余元素？
在直角三角形中，如果知道了五个元素中的两个元素（至少有一个是边），就可以求出其余的三个元素。在直角三角形中，除直角外，由已知元素求出未知元素的过程，叫做解直角三角形。
例1、 如图，在Rt△ABC中，∠C＝90°， 解这个直角三角形。（精确到0.1）
∠A=90°-42°6 ’=47°54 ’
b还有其它求法吗？哪种求法更合适？
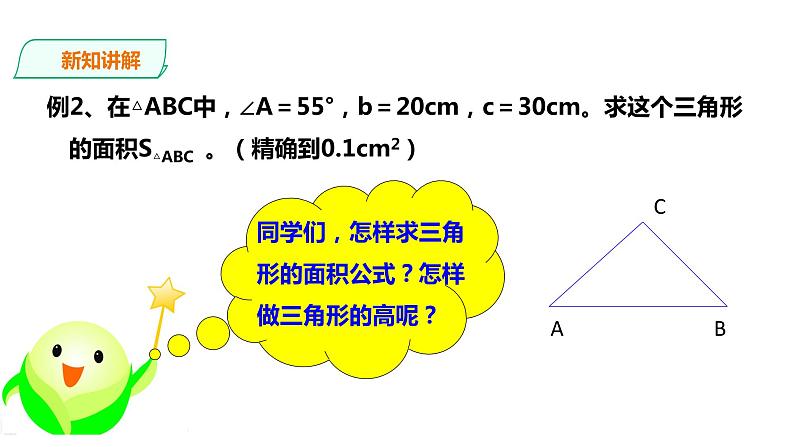
例2、在△ABC中，∠A＝55°，b＝20cm，c＝30cm。求这个三角形的面积S△ABC 。（精确到0.1cm2）
同学们，怎样求三角形的面积公式？怎样做三角形的高呢？
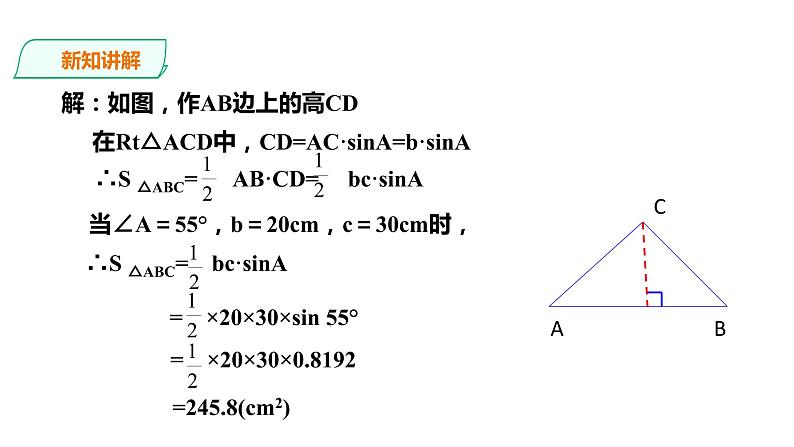
解：如图，作AB边上的高CD
在Rt△ACD中，CD=AC·sinA=b·sinA
∴S △ABC= AB·CD= bc·sinA
当∠A＝55°，b＝20cm，c＝30cm时，
∴S △ABC= bc·sinA
= ×20×30×sin 55°
=245.8(cm2)
= ×20×30×0.8192
从上题的解法，我们可以得出求三角形面积的新的方法吗？△ABC的面积是否可以用a、c及夹角B或a、b及夹角C表示呢？
S △ABC = bc·sinA = ab·sinC = ac·sinB
如图，在Rt△ABC中，∠C＝90°，根据下列条件解直角三角形；（1）a = 30 , b = 20 ; (2) ∠B＝72°，c = 14.
（1）a = 30 , b = 20
(2) ∠B＝72°，c = 14.
当三角形的形状题中没有说明时，记得一定要注意分类讨论哦！
当△ABC为钝角三角形时，如图①，
∵AC=13，∴由勾股定理，得CD=5
∴BC=BD-CD=12-5=7；
当△ABC为锐角三角形时，如图②，BC=BD+CD=12+5=17.
∴BC的长为7或17.
只要知道五个元素中的两个元素（至少有一个是边），就可以求出余下的三个未知元素
23.2.1 解直角三角形1、解直角三角形的依据2、解直角三角形的解法