初中数学沪科版九年级上册22.3 相似三角形的性质优质课课件ppt

这是一份初中数学沪科版九年级上册22.3 相似三角形的性质优质课课件ppt，共22页。PPT课件主要包含了新知导入，由等比性质得，课堂练习，中考链接，驶向胜利的彼岸，课堂总结，定理1，相似三角形的性质，定理2，定理3等内容，欢迎下载使用。

（1）什么叫相似三角形？（2）到目前为止，我们已经学过的证明三角形相似的方法有哪些呢?
（1）什么叫相似三角形？
对应角相等、对应边成比例的三角形,叫做相似三角形。
1、定义2、相似三角形判定的定理：平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似。3、定理1：两个角对应相等的两个三角形相似。4、定理2：两边成比例且夹角相等的两个三角形相似。
（2）到目前为止，我们已经学过的证明三角形相似的方法有哪些呢?
5、定理3：三边成比例的两个三角形相似。6、直角三角形相似的定理：如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例， 那么这两个直角三角形相似。
我们知道，两个三角形相似，它们的对应角相等，对应边成比例，除此之外，两个相似三角形还有哪些性质呢？
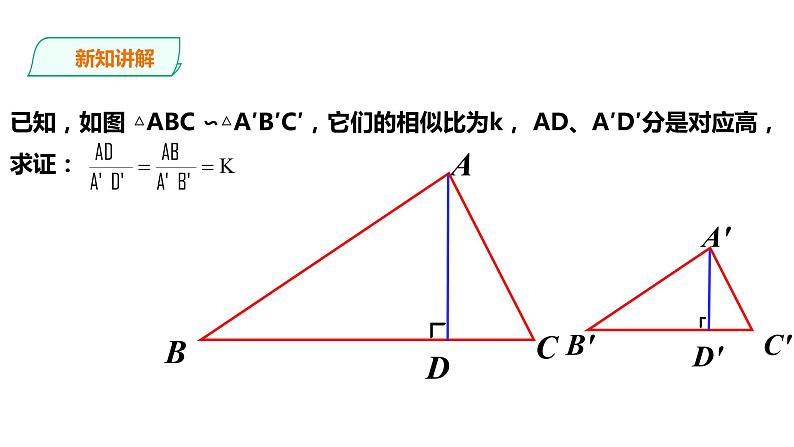
已知，如图 △ABC ∽△A′B′C′，它们的相似比为k， AD、A′D′分是对应高，求证：
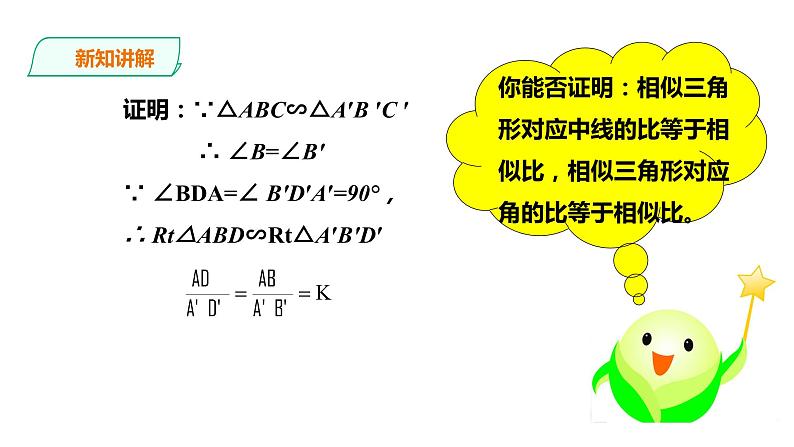
证明：∵△ABC∽△A′B ′C ′ ∴ ∠B=∠B′∵ ∠BDA=∠ B′D′A′=90°，∴ Rt△ABD∽Rt△A′B′D′
你能否证明：相似三角形对应中线的比等于相似比，相似三角形对应角的比等于相似比。
定理1 相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比。
我们知道，如果△ABC∽△ A′B′C′，且相似比为k，那么
两个相似三角形的周长比会等于相似比吗？
定理2 相似三角形周长的比等于相似比

如果 △ABC和△A′B′C′相似，它们的相似比为k，AD、A′D′分别为对应高，根据三角形面积计算公式及定理1，得
定理3 相似三角形面积比等于相似比的平方。
例1 一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm.要把它加工成矩形零件,使矩形的长,宽之比为2:1,并且矩形长的一边位于边BC上,另两个顶点分别在边AB,AC上,求这个矩形零件的边长。
解:因为矩形PQRS为加工成的矩形零件,边SR在BC上,顶点P,Q分别在AB,AC上,△ABC的高AD交PQ于点E,所以设PS为xcm,则PQ为2xcm.
答：这个矩形零件的边长分别是48cm和24cm.
∵PQ//BC,∴△APQ∽△ABC ∴即解方程，得 x=24， 2x=48
例2 如图,△ABC 的面积为25，直线DE平行于BC分别交AB,AC于点D，E , 如果 △ADE的面积为9，求 的值.
∴ △ADE ∽△ABC.
解 ∵ DE//BC，
如图，将△ABC沿BC方向平移得到△DEF，△ABC与△DEF重叠部分的面积是△ABC的面积的一半.已知BC=2，求△ABC平移的距离。 　
解：根据题意，可知EG∥AB.
∴∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC
即，△ABC平移的距离为
如图，梯形ABCD中，AD∥BC，∠B＝∠ACD＝90°，AB＝2，DC＝3，则△ABC与△DCA的面积比为(　 　)
A．2∶3　　　　　 B． 2∶5　　　　 C．4∶9　　　　 D. ∶
解析：∵AD//BC，∴∠ACB＝∠CAD.又∵∠B＝∠ACD＝90°，∴△ABC∽△DCA.∵AB＝2，DC＝3，∴S△ABC∶S△DCA＝AB 2∶CD 2＝4∶9.故选C.
相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比。
相似三角形周长的比等于相似比。
相似三角形面积比等于相似比的平方。
22.3 相似三角形的性质定理1 相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比。定理2 相似三角形周长的比等于相似比。定理3 相似三角形面积比等于相似比的平方。