初中数学沪科版九年级上册22.5 综合与实践 测量与误差优质课ppt课件

这是一份初中数学沪科版九年级上册22.5 综合与实践 测量与误差优质课ppt课件，共25页。PPT课件主要包含了新知导入，-----，课堂练习，中考链接，驶向胜利的彼岸，课堂总结，综合与实践，板书设计等内容，欢迎下载使用。
五星红旗，是新中国的象征，也是中华民族的骄傲
在学校的操场上，有一根不锈钢旗杆，在既不攀爬到旗杆顶上，又不破坏旗杆的情况下，要求测量出旗杆的高度呢？
下面有四种测量方法，测量中可使用的工具有：皮尺、测角器、1米竿（长度为1m的竹竿）、镜子、长竿（长度大于人身高的竹竿）.
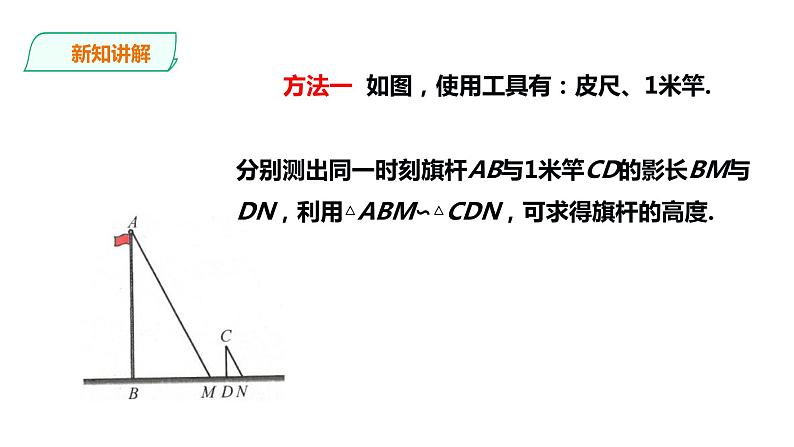
方法一 如图，使用工具有：皮尺、1米竿. 分别测出同一时刻旗杆AB与1米竿CD的影长BM与DN，利用△ABM∽△CDN，可求得旗杆的高度.
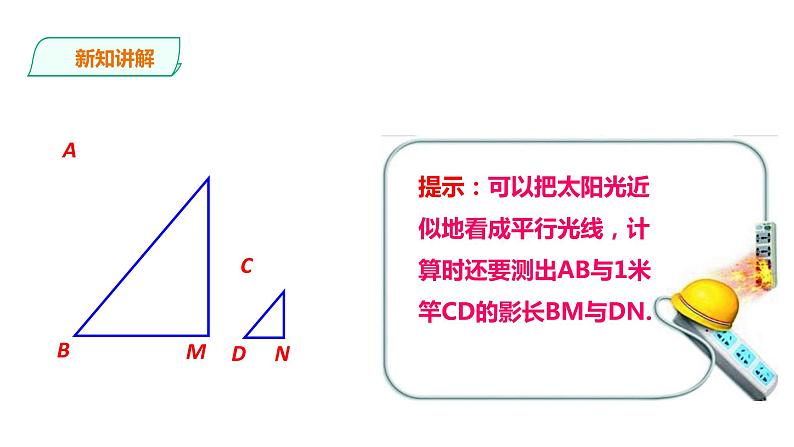
提示：可以把太阳光近似地看成平行光线，计算时还要测出AB与1米竿CD的影长BM与DN.
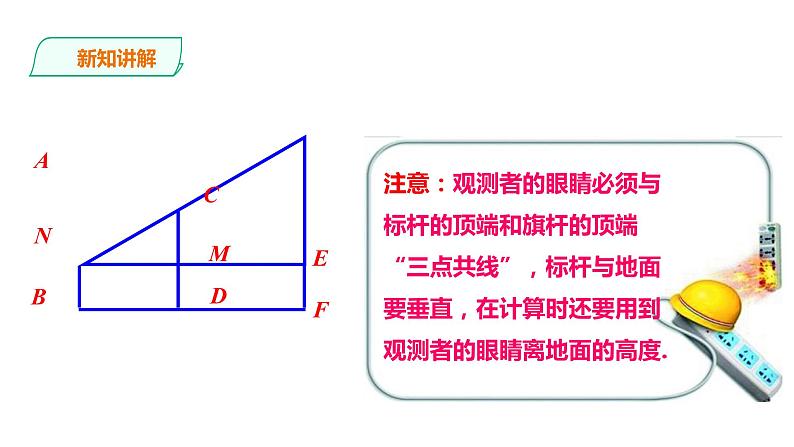
方法二 如图，使用工具有：皮尺、长竿. 将长竿立于旗杆与人之间，观察长竿和旗杆顶端，使人的眼睛E 与A,C 在同一直线上，利用△ANE∽△CME，可求得旗杆的高度.
注意：观测者的眼睛必须与标杆的顶端和旗杆的顶端“三点共线”，标杆与地面要垂直，在计算时还要用到观测者的眼睛离地面的高度.
方法三 如图，使用工具有：皮尺、镜子. 将镜面朝上置于地面C 处，观察镜子中旗杆顶端A‘，使人的眼睛E 与C，A' 在 同一直线上，利用△ABC ≌△A'BC，△A'BC∽△EFC，可求得旗杆的高度.
注意：将镜面朝上置于地面C 处，观察镜子中旗杆顶端，使人的眼睛E 与C，A’ “三点共线”。
方法四 如图，使用工具有：皮尺、测角器. 通过测角器观察旗杆顶端A，使测角器的示数为60°（条件允许可以是45°、30°），利用AB=AM+BM= ，可求得旗杆的高度.
---------------
注意：用测角器测量角度时，多次测量求平均值。
问题1 请你用这四种方法进行旗杆测量，并将测量数据记录于下列表格中
活动探究：思考以下问题，动手做一做。（小组讨论，3min）
问题2 你觉得何种方法操作简便，又是何种方法测得的数据更准确？你还有其他的测量方法吗？问题3 在测量中，每次的测量数据都有差异，你是如何处理的，你测量了几次？问题4 几种测量方法为何有误差，如何改进？请对测量误差进行思考，查找误差原因。
减小误差的方法：尽量使用精密的测量仪器，采用多次测量的结果的平均值作为测量的结果，测量时步骤必须标准。
古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O’B’,比较棒子的影长A’B’ 与金字塔的影长AB,即可近似算出金字塔的高度OB. 如果O’B’=1， A’B’ =2，AB=274，求金字塔的高度OB.
解　 由于太阳光是平行光线，∴ ∠OAB＝∠O′A′B′．
又∵ ∠ABO＝∠A′B′O′＝90°． ∴ △OAB∽△O′A′B′，  
∴ OB∶O′B′＝AB∶A′B′，  
即该金字塔高为137米．  
某学校在“行读石鼓阁”研学活动中，参观了中华石鼓园，石鼓阁是宝鸡城市新地标．建筑面积7 200平方米，为我国西部第一高阁．秦汉高台门阙的建筑风格，追求稳定之中的飞扬灵动，深厚之中的巧妙组合，使景观功能和标志功能融为一体。
如图，李梅在小亮和“石鼓阁”之间的直线BM上平放一平面镜，在镜面上做了一个标记，这个标记在直线BM上的对应位置为点C，镜子不动，李梅看着镜面上的标记，她来回走动，走到点D时，看到“石鼓阁”顶端点A的镜面中的像与镜面上的标记重合，这时，测得李梅眼睛与地面的高度ED＝1.6米，CD＝2.2米
然后，在阳光下，小亮从D 点沿DM 方向走了29.4米，此时“石鼓阁”影子与小亮的影子顶端恰好重合，测得小亮身高1.7米，影长FH＝3.4米．已知AB⊥BM，ED⊥BM，GF⊥BM，其中，测量时所使用的平面镜的厚度忽略不计，请你根据图中提供的相关信息，求出“石鼓阁”的高AB的长度。
解：设AB＝x m，由题意可得∠ACB＝∠ECD，∠ABC＝∠EDC，则△ABC∽△EDC，∴ ， 即 ，则
由题意得GF//AB，∴△GFH∽△ABH，∴ ，即 ，则 ，解得 x＝50.56.答：“石鼓阁”的高AB的长度为50.56 m.
22.5 综合与实践--测量与误差1、测量的方法2、误差