初中数学沪科版九年级上册23.2解直角三角形及其应用优质课件ppt

这是一份初中数学沪科版九年级上册23.2解直角三角形及其应用优质课件ppt，共23页。PPT课件主要包含了新知导入，铅垂线，水平线，新知讲解，图23-16，图23-17，解方程得，图23-18，课堂练习，在Rt△ACD中等内容，欢迎下载使用。
1、亲爱的同学们，什么叫解直角三角形？2、解直角三角形常用关系是什么？
1、什么叫解直角三角形？在直角三角形中，除直角外，由已知元素求出未知元素的过程，叫做解直角三角形。
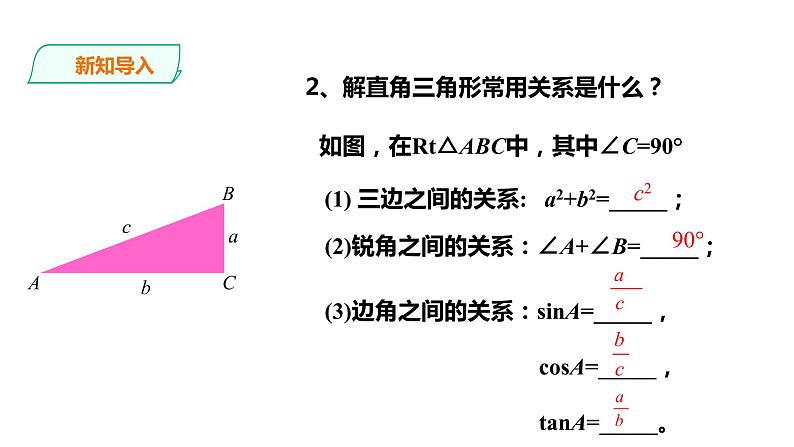
(1) 三边之间的关系: a2+b2=_____；
(2)锐角之间的关系：∠A+∠B=_____；
(3)边角之间的关系：sinA=_____， csA=_____， tanA=_____。
如图，在Rt△ABC中，其中∠C=90°
2、解直角三角形常用关系是什么？
同学们，解直角三角形在实际生活中怎样应用呢？
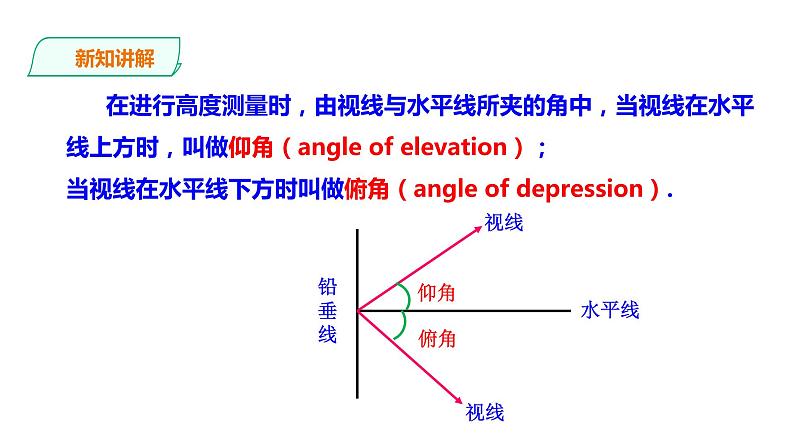
在进行高度测量时，由视线与水平线所夹的角中，当视线在水平线上方时，叫做仰角（angle f elevatin）；当视线在水平线下方时叫做俯角（angle f depressin）.
例3 如图 23-16，一学生要测量校园内一棵水杉树的高度。他站在距离水杉树8米的E处,测得树顶的仰角∠ACD=52°,已知测角器的架高CE=1.6m，问树高AB为多少米？(精确到0.1m).
AD=CD ·tan∠ACD=8·tan52° =8×1.2799≈10.2(m). 由DB=CE=1.6m，得∴AB=AD+DB＝10.2＋１.6≈11.8(m).
答:树高AB为11.8米.
解 在Rt △ACD中，∠ACD=52° CD=EB=8m，
由 tan∠ACD= 得
例4 解决本章引言所提问题。如图23-17，某校九年级学生要测量当地电视塔的高度AB，因为不能直接到达塔底B处，他们采用在发射台院外与电视塔底B成一直线的C，D两处地面上，用测角器测得电视塔顶部A的仰角分别为45°和30°,同时量得CD为50m，已知测角器高为1m，问电视塔的高度为多少米？(结果精确到1m).
解 设AB1=xm在Rt △AC1B1中，由∠AC1B1=45°，得 C1B1=AB1在Rt △AD1B1中，由∠AD1B1=30°，得
由 tan∠ AD1B1 = ， 即
x=25( +1 ) ≈68∴ AB= AB1 +B1B ≈68+1 =69（m）
答：电视塔的高度为69m
例5 如图23-18，一船以20n mile/h的速度向东航行，在A处测得灯塔C在北偏东60°的方向上，继续航行1h到达B处，再测得灯塔C在北偏东30°的方向上，已知灯塔C四周10 n mile 内有暗礁，问这船继续向东航行是否安全？
分析：这船继续向东航行是否安全，取决于灯塔C到AB航线的距离是否大于10 n mile
解 过点C作CD⊥AB于点D，设CD=x n mile在Rt △ACD中，AD=在Rt △BCD中，BD=
由AB=AD-BD，得 即解方程，得
答：这船继续向东航行是安全的。
解直角三角形应用的基本图形①不同地点看同一点(如图 ①)；②同一地点看不同点(如图 ②)
建筑物BC上有一旗杆AB，由距BC 40m的D处观察旗杆顶部A的仰角54°，观察底部B的仰角为45°，求旗杆的高度（精确到0.1m）
解：在等腰三角形BCD中∠ACD=90°，BC=DC=40m，
所以AB=AC－BC=55.2－40=15.2m
答：棋杆的高度为15.2m.
AC=CD∙tan54̊
如图，某校数学兴趣小组为测得大厦AB的高度，在大厦前的平地上选择一点C，测得大厦顶端A的仰角为30°，再向大厦方向前进80米，到达点D处(C，D，B三点在同一直线上)，又测得大厦顶端A的仰角为45°，请你计算该大厦的高度(精确到0.1米，参考数据： ≈ 1.414， ≈1.732)．
解：在Rt△ABD中，∵∠BDA＝90°，∠BAD＝30°，AD＝42 m，∴BD＝AD·tan30°＝42× ＝14 (m)．在Rt△ACD中，∠ADC＝90°，∠CAD＝60°，∴CD＝AD·tan60°＝42× ＝42 (m)，∴BC＝BD＋CD＝14 ＋42 ＝56 (m)．答：这栋楼的高度为56 m.
注意：解直角三角形在几何中的应用，关键是通过作垂线的方法，合理地构造出将已知元素和未知元素包含在内的直角三角形，分析已知量与未知量在这个三角形中的联系。
利用解直角三角形的知识解决实际问题的一般过程是:
1.将实际问题转化为数学问题;
(命题角度：求某建筑物或飞行器的高度(或宽度)；画出平面图形,转化为解直角三角形的问题)
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形
23.2.2 解直角三角形1、仰角和俯角2、解决实际问题的一般过程