人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式第一课时导学案

这是一份人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式第一课时导学案，共8页。学案主要包含了知识点一，知识点二，知识点三，知识点四，例3-1，例3-2，参考答案，自我检测1等内容，欢迎下载使用。

导学目标：


1．从函数观点看一元二次方程．会结合一元二次函数的图象，求解一元二次方程．


2．从函数观点看一元二次不等式．会结合一元二次函数图像，求解一元二次不等式．


3．借助一元二次函数的图象，了解一元二次不等式、方程与其相应函数的联系．


（预习教材P51~ P53，回答下列问题）


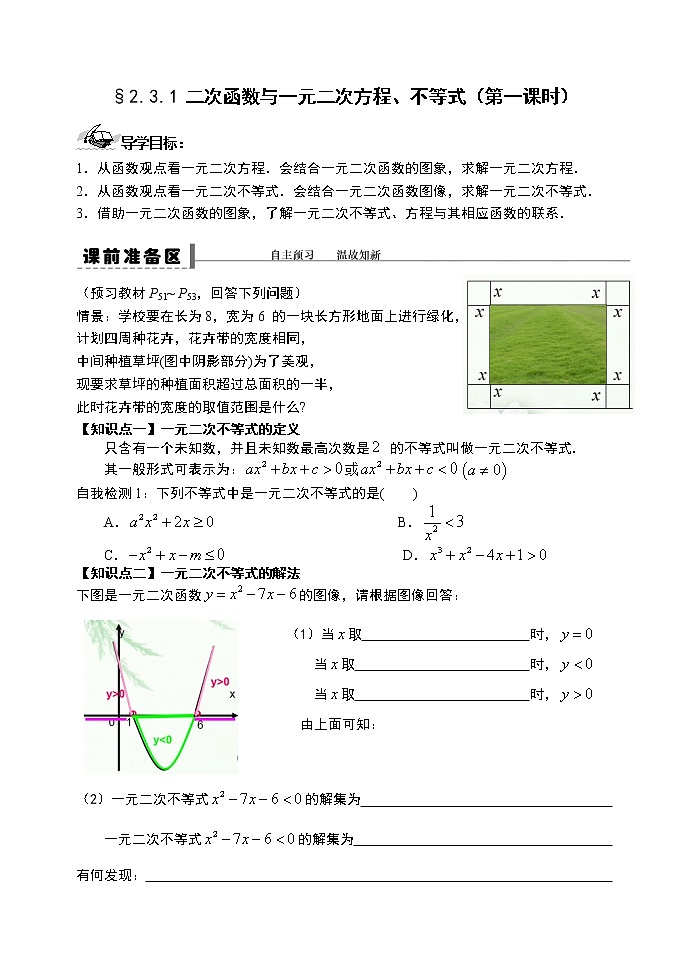
情景：学校要在长为8，宽为6 的一块长方形地面上进行绿化，


计划四周种花卉，花卉带的宽度相同，


中间种植草坪(图中阴影部分)为了美观，


现要求草坪的种植面积超过总面积的一半，


此时花卉带的宽度的取值范围是什么?


【知识点一】一元二次不等式的定义


只含有一个未知数，并且未知数最高次数是 的不等式叫做一元二次不等式.


其一般形式可表示为：或


自我检测1：下列不等式中是一元二次不等式的是( )


A． B．


C． D．


【知识点二】一元二次不等式的解法


下图是一元二次函数的图像，请根据图像回答：


（1）当取 时，


当取 时，


当取 时，


由上面可知：





（2）一元二次不等式的解集为


一元二次不等式的解集为


有何发现：


（3）一元二次方程的解集为


有何发现：


请归纳求解一元二次不等式的解集的步骤？














自我检测2：一元二次不等式的解集是


【知识点三】三个二次之间的关系


请根据右图回答：


一元二次方程、


一元二次不等式


与其对应的一元二次函数图像的关系？


（1）一元二次方程的两根为是一元二次函数图像与轴 ．


（2）一元二次方程的解集的端点是一元二次方程的 ．


（3）一元二次方程的两根为，则 ．


自我检测3：不等式的解集为，则a，c的值分别为( )


A．a＝6，c＝1 B．a＝－6，c＝－1


C．a＝1，c＝1 D．a＝－1，c＝－6


【知识点四】一元二次不等式恒成立问题


（1）恒成立的充要条件是：且．


（2）恒成立的充要条件是：且．


自我检测4：若一元二次不等式对一切实数x都成立，则k的取值范围？








题型一 一元二次不等式的解法


【例1】求解下列一元二次不等式


(1)求不等式的解集．


(2)求不等式的解集．


(3)求不等式的解集．























题型二 三个“二次”之间的关系


【例2】已知关于x的不等式的解集为，求关于x的不等式的解集．























题型三 一元二次不等式恒成立问题


【例3-1】要使函数的值恒为负值，求的取值范围．











【例3-2】当x(1,2)时，不等式x2＋mx＋4<0恒成立，求m的取值范围．








1．一元二次不等式的解集是（ ）


A．{x|x<−1} B．


C． D．


2．若不等式的解集为R，则实数m的取值范围是( )


A．(2，＋∞) B．(－∞，2)


C．(－∞，0)∪(2，＋∞) D．(0,2)





3．求解下列一元二次不等式


(1) ； (2) ；


(3) ； (4)



































4．一元二次不等式的解集为，求不等式的解集．

















【参考答案】


学后反思 巩固提高





情景：设花卉带的宽为，则依题意可得：


，整理得．


【自我检测1】答案：C


（1）或； ；或


（2）；


函数位于轴上方的图像对应的的取值即为该函数所对应的不等式大于0的解集；


函数位于轴下方的图像对应的的取值即为该函数所对应的不等式小于0的解集；


（3）


函数图像与轴交点的横坐标即为该函数所对应的方程的解；
























































解一元二次不等式的一般步骤


（1）一化：把不等式变形为二次项系数大于零的标准形式．


（2）二判：计算对应方程的判别式．


（3）三求：求出对应的一元二次方程的根，或根据判别式说明方程有没有实根．


（4）四写：利用“大于取两边，小于取中间”写出不等式的解集．


【自我检测2】答案：


（1）一元二次方程的两根为是一元二次函数图像与轴交点的横坐标．


（2）一元二次方程的解集的端点是一元二次方程的两根．


（3）一元二次方程的两根为，则．


【自我检测3】答案：B


（1）恒成立的充要条件是：且．


（2）恒成立的充要条件是：且．


【自我检测4】答案：





【例1】答案：（1）{x|x<2，或x>3}；（2）eq \b\lc\{\rc\ (\a\vs4\al\c1(x\b\lc\|\rc\}(\a\vs4\al\c1(x≠\f(1,3)))))；（3）．



































【例2】答案：由不等式ax2＋bx＋c>0的解集为{x|20，即x2－eq \f(5,6)x＋eq \f(1,6)>0，解得xeq \f(1,2)，所以不等式cx2＋bx＋a<0的解集为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x＜\f(1,3)或x＞\f(1,2)))))．


【例3-1】函数的值恒为负值，即不等式对一切实数x都成立，于是


①当时，恒成立；


②当时，要使其恒成立，则有，解得.


综上，的取值范围为.


【例3-2】解法一：∵不等式x2＋mx＋4<0对x(1,2)恒成立，∴mx<−x2−4对x(1,2)恒成立，即m<−对x(1,2)恒成立，令y=，∵函数y=在x(1,2)上是减函数，∴4

∴−5<−<−4，∴m≤−5.


解法二：设f (x)=x2＋mx＋4，当x(1,2)时，f (x)<0恒成立⇔ .





1．一元二次不等式−2x2＋x＋3<0的解集是（ ）


A．{x|x<−1} B．


C． D．


答案：D


2．若不等式x2＋mx＋eq \f(m,2)>0的解集为R，则实数m的取值范围是( )


A．(2，＋∞) B．(－∞，2)


C．(－∞，0)∪(2，＋∞) D．(0,2)


答案：D





3．求解下列一元二次不等式


(1)x2－7x＋12>0； (2)－x2－2x＋3≥0；


(3)x2－2x＋1<0； (4)－2x2＋3x－2<0.





答案：(1) {x|x＜3或x＞4}．(2) {x|－3≤x≤1}．


(3) (4)





4．一元二次不等式x2＋px＋q<0的解集为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(－\f(1,2)0的解集．


答案：因为x2＋px＋q<0的解集为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(－\f(1,2)

所以x1＝－eq \f(1,2)与x2＝eq \f(1,3)是方程x2＋px＋q＝0的两个实数根，


由根与系数的关系得eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(1,3)－\f(1,2)＝－p，,\f(1,3)×\b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)))＝q，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(p＝\f(1,6)，,q＝－\f(1,6).))


所以不等式qx2＋px＋1>0即为－eq \f(1,6)x2＋eq \f(1,6)x＋1>0，


整理得x2－x－6<0，解得－2

即不等式qx2＋px＋1>0的解集为{x|－2