数学必修第一册第三章函数概念与性质3.2 函数的基本性质精品第一课时练习

展开

这是一份数学必修第一册第三章函数概念与性质3.2 函数的基本性质精品第一课时练习，共7页。试卷主要包含了函数等内容，欢迎下载使用。

一．选择题

1．下列图象表示的函数中，在R上是增函数的是（）

A． B． C． D．

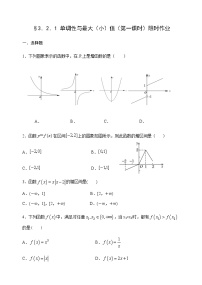
2．函数在区间上的图象如图所示，则此函数的增区间是（）

A．B．

C．D．

3．函数的增区间是( )

A．(－∞，1] B．[2，＋∞)

C．(－∞，1]，[2，＋∞) D．(－∞，＋∞)

4．下列函数中，满足对任意，当x1

A． B．

C．D．

5．若函数为上的增函数，则实数的值为（）

A．B．

C．D．

6．函数 ( )

A．在(－1，＋∞)上单调递增 B．在(1，＋∞)上单调递增

C．在(－1，＋∞)上单调递减 D．在(1，＋∞)上单调递减

7．函数在区间是减函数，则实数a的取值范围是（）

A．B．

C．D．

8．函数在R上为增函数，且，则实数m的取值范围( )

A．(－∞，－3) B．(0，＋∞)

C．(3，＋∞) D．(－∞，－3)∪(3，＋∞)

二．填空题

9．如图所示为函数y＝f(x)，x∈[－4,7]的图象，则函数f(x)的单调递增区间是____________．

10．函数的单调减区间为________．

三．解答题

11．判断并证明函数在(0，＋∞)上的单调性．

12．已知f(x)是定义在[－1,1]上的增函数，且f(x－2)

§3．2．1 单调性与最大（小）值（第一课时）限时作业

【参考答案】

一．选择题

1．下列图象表示的函数中，在R上是增函数的是（）

A． B． C． D．

【答案】D

2．函数在区间上的图象如图所示，则此函数的增区间是（）

A．B．

C．D．

【答案】C

3．函数的增区间是( )

A．(－∞，1] B．[2，＋∞)

C．(－∞，1]，[2，＋∞) D．(－∞，＋∞)

【答案】C

4．下列函数中，满足对任意，当x1

A． B．

C．D．

【答案】B

5．若函数为上的增函数，则实数的值为（）

A．B．

C．D．

【答案】D

6．函数 ( )

A．在(－1，＋∞)上单调递增 B．在(1，＋∞)上单调递增

C．在(－1，＋∞)上单调递减 D．在(1，＋∞)上单调递减

【答案】B

7．函数在区间是减函数，则实数a的取值范围是（）

A．B．

C．D．

【答案】B

8．函数在R上为增函数，且，则实数m的取值范围( )

A．(－∞，－3) B．(0，＋∞)

C．(3，＋∞) D．(－∞，－3)∪(3，＋∞)

【答案】C

二．填空题

9．如图所示为函数y＝f(x)，x∈[－4,7]的图象，则函数f(x)的单调递增区间是____________．

【答案】[－1．5,3]和[5,6]

10．函数的单调减区间为________．

【答案】(－∞，0]，[2,4]

三．解答题

11．判断并证明函数f(x)＝－eq \f(1,x)＋1在(0，＋∞)上的单调性．

【答案】函数f(x)＝－eq \f(1,x)＋1在(0，＋∞)上是增函数．证明如下：

设x1，x2是(0，＋∞)上的任意两个实数，且x1

f(x1)－f(x2)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,x1)＋1))－eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,x2)＋1))＝eq \f(x1－x2,x1x2)，

由x1，x2∈(0，＋∞)，得x1x2>0，

又由x1

于是f(x1)－f(x2)<0，

即f(x1)

∴f(x)＝－eq \f(1,x)＋1在(0，＋∞)上是增函数．

12．已知f(x)是定义在[－1,1]上的增函数，且f(x－2)

【答案】∵f(x)是定义在[－1,1]上的增函数，

且f(x－2)

∴eq \b\lc\{\rc\ (\a\vs4\al\c1(－1≤x－2≤1，,－1≤1－x≤1，,x－2<1－x，))解得1≤x

所以x的取值范围为1≤x

相关试卷更多