初中数学浙教版九年级下册第三章 投影与三视图3.4 简单几何体的表面展开图第3课时精练
展开若圆锥的底面半径为r,母线为l,圆锥的侧面展开图扇形的圆心角为θ,则:
(1)S锥侧=________,S锥全=________;
(2)θ=____________.
A组 基础训练
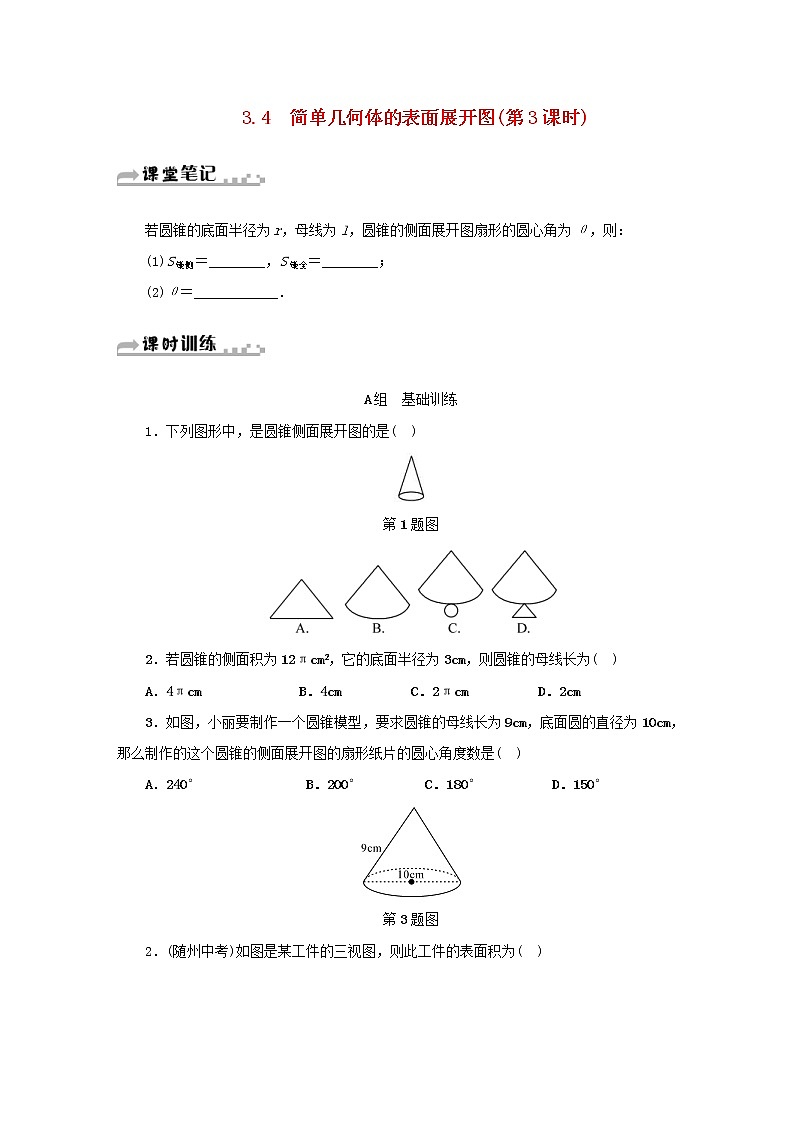
下列图形中,是圆锥侧面展开图的是( )
第1题图
2.若圆锥的侧面积为12πcm2,它的底面半径为3cm,则圆锥的母线长为( )
A.4πcm B.4cm C.2πcm D.2cm
3.如图,小丽要制作一个圆锥模型,要求圆锥的母线长为9cm,底面圆的直径为10cm,那么制作的这个圆锥的侧面展开图的扇形纸片的圆心角度数是( )
A.240° B.200° C.180° D.150°
第3题图
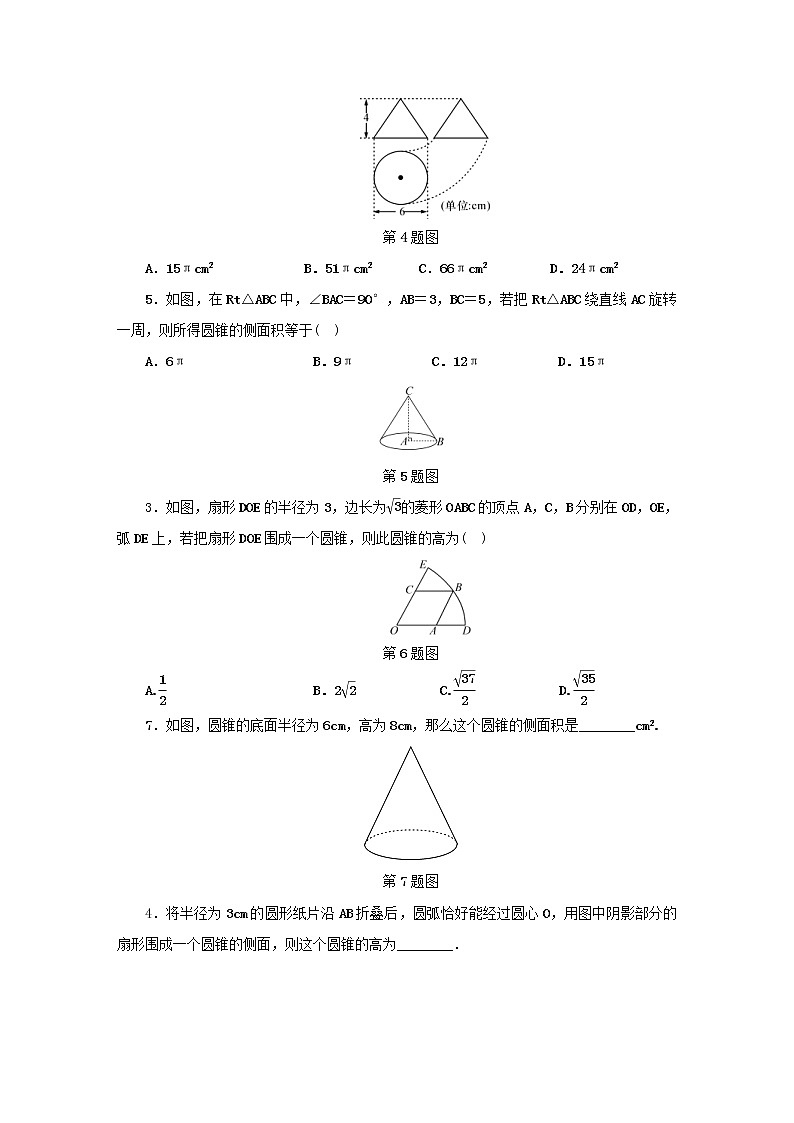
(随州中考)如图是某工件的三视图,则此工件的表面积为( )
第4题图
A.15πcm2 B.51πcm2 C.66πcm2 D.24πcm2
5.如图,在Rt△ABC中,∠BAC=90°,AB=3,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )
A.6π B.9π C.12π D.15π
第5题图
如图,扇形DOE的半径为3,边长为eq \r(3)的菱形OABC的顶点A,C,B分别在OD,OE,弧DE上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
第6题图
A.eq \f(1,2) B.2eq \r(2) C.eq \f(\r(37),2) D.eq \f(\r(35),2)
7.如图,圆锥的底面半径为6cm,高为8cm,那么这个圆锥的侧面积是________cm2.
第7题图
将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为________.
第8题图
9.(齐齐哈尔中考)一个侧面积为16eq \r(2)πcm2的圆锥,其主视图为等腰直角三角形,则这个圆锥的高为________cm.
10.已知一个圆锥沿轴剖开是一个等腰三角形.若这个三角形的底为8cm,腰为10cm.
(1)求圆锥侧面展开图的扇形弧长;
(2)求圆锥的表面积.
B组 自主提高
11.若一个圆锥的侧面积是10,圆锥母线l与底面半径r之间的函数关系图象大致是(D)
12.已知圆锥的轴截面是等边三角形,则它的侧面展开图的扇形圆心角为________.
13.“神舟五号”太空仓的示意图如图所示.太空仓的外表面须做特别处理,以承受重返地球大气层时因空气摩擦而产生的高热.求该太空仓要接受防高热处理的面积(结果精确到0.1m2).
第13题图
C组 综合运用
14.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)分别以直线AC,BC为轴,把△ABC旋转一周,得到两个不同的圆锥,求这两个圆锥的侧面积;
(2)以直线AB为轴,把△ABC旋转一周,求所得几何体的表面积.
第14题图
3.4 简单几何体的表面展开图(第3课时)
【课堂笔记】
(1)πrl πrl+πr2 (2)eq \f(r,l)×360°
【课时训练】
1-5.BBBDD
6.D
7.60π
8.2eq \r(2)cm
9.4
(1)l弧=πd=8πcm; (2)S表=πrl+πr2=40π+16π=56πcm2.
D
180°
圆锥母线l=eq \r(2.12+22)=eq \r(8.41)=2.9m,S表=πrl+2πrh+πr2=17.8π≈55.9m2.
14.(1)∵∠C=90°,AC=6,BC=8,∴AB=eq \r(AC2+BC2)=10,所以以直线AC为轴,把△ABC旋转一周,得到的圆锥的侧面积=π×8×10=80π;以直线BC为轴,把△ABC旋转一周,得到的圆锥的侧面积=π×6×10=60π;
(2)作CD⊥AB于点D,∵eq \f(1,2)CD·AB=eq \f(1,2)AC·BC,∴CD=eq \f(6×8,10)=eq \f(24,5),以直线AB为轴,把△ABC旋转一周,所得几何体是以CD为底面半径的两个圆锥,则它的表面积=π×eq \f(24,5)×8+π×eq \f(24,5)×6=eq \f(336,5)π.
浙教版九年级下册第三章 投影与三视图3.4 简单几何体的表面展开图精品一课一练: 这是一份浙教版九年级下册第三章 投影与三视图3.4 简单几何体的表面展开图精品一课一练,共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学浙教版九年级下册第三章 投影与三视图3.4 简单几何体的表面展开图当堂检测题: 这是一份初中数学浙教版九年级下册第三章 投影与三视图3.4 简单几何体的表面展开图当堂检测题,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学浙教版九年级下册3.4 简单几何体的表面展开图综合训练题: 这是一份初中数学浙教版九年级下册3.4 简单几何体的表面展开图综合训练题,共16页。试卷主要包含了0分),【答案】C,【答案】B,【答案】D,【答案】A等内容,欢迎下载使用。