

浙教版九年级下册1.3 解直角三角形第2课时同步达标检测题
展开1.坡度,坡角的定义:如图,通常把坡面的铅直高度h和水平宽度l之比叫________,用字母i表示,把坡面与水平面的夹角叫做________,记做α,于是i=________=tanα,显然,坡度越大,α角越大,坡面就越陡.
2.三角形面积S=eq \f(1,2)absinC=eq \f(1,2)acsinB=eq \f(1,2)bcsinA.
A组 基础训练
1.如图,斜坡AB与水平面的夹角为α,下列命题中,不正确的是( )
第1题图
A.斜坡AB的坡角为α
B.斜坡AB的坡度为eq \f(BC,AB)
C.斜坡AB的坡度为tanα
D.斜坡AB的坡度为eq \f(BC,AC)
2.如图,C、D是以AB为直径的半圆上两个点(不与A、B重合).连DC、AC、DB,AC与BD交于点P.若∠APD=α,则eq \f(CD,AB)=( )
A.sinα B.csα C.tanα D.eq \f(1,tanα)
第2题图
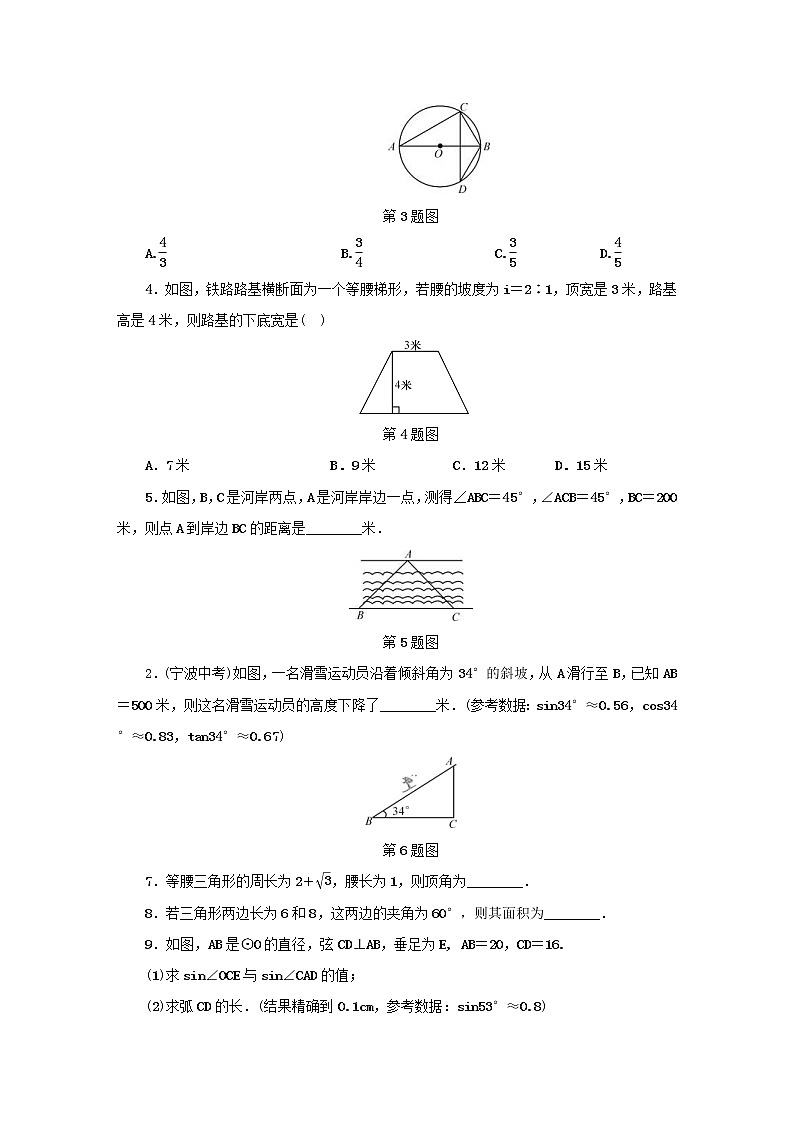
如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,则sin∠ABD的值为( )
第3题图
A.eq \f(4,3) B.eq \f(3,4) C.eq \f(3,5) D.eq \f(4,5)
4.如图,铁路路基横断面为一个等腰梯形,若腰的坡度为i=2∶1,顶宽是3米,路基高是4米,则路基的下底宽是( )
第4题图
A.7米 B.9米 C.12米 D.15米
5.如图,B,C是河岸两点,A是河岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=200米,则点A到岸边BC的距离是________米.
第5题图
(宁波中考)如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了________米.(参考数据:sin34°≈0.56,cs34°≈0.83,tan34°≈0.67)
第6题图
7.等腰三角形的周长为2+eq \r(3),腰长为1,则顶角为________.
8.若三角形两边长为6和8,这两边的夹角为60°,则其面积为________.
9.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E, AB=20,CD=16.
(1)求sin∠OCE与sin∠CAD的值;
(2)求弧CD的长.(结果精确到0.1cm,参考数据:sin53°≈0.8)
第9题图
10.如图,有一段斜坡BC长10米,坡角∠CBD=12°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.
(1)求坡高CD;
(2)求斜坡新起点A到原起点B的距离(精确到0.1米,参考数据:sin12°≈0.21,cs12°≈0.98,tan5°≈0.09)
第10题图
B组 自主提高
11.如图,四边形ABCD的对角线AC、BD的长分别为m、n,当AC与BD所夹的锐角为θ时,则四边形ABCD的面积S=____________.(用含m,n,θ的式子表示)
第11题图
12.如图,一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m.已知木箱高BE=eq \r(3)m,斜面坡角为30°,求木箱端点E距地面AC的高度EF.
第12题图
13.如图,一棵树AB的顶端A的影子落在教学楼前的坪地C处,小明分别测得坪地、台阶和地面上的三段影长CE=1m,DE=2m,BD=8m,DE与地面的夹角α=30°.在同一时刻,已知一根1m长的直立竹竿在地面上的影长恰好为2m,请你帮助小明根据以上数据求出树AB的高.(结果精确到0.1m,参考数据:eq \r(2)≈1.41,eq \r(3)≈1.73)
第13题图
C组 综合运用
14.为了缓解停车难的问题,某单位拟建地下停车库,建筑设计师提供的该地下停车库的设计示意图如图所示.按照规定,地下停车库坡道上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE的长度(精确到0.1m,参考数据:tan18°≈0.3249,cs18°≈0.9511).
第14题图
参考答案
1.3 解直角三角形(第2课时)
【课堂笔记】
1.坡度 坡角 eq \f(h,l)
【课时训练】
1-4.BBDA
5.100
6.280
7.120°
8.12eq \r(3)
(1)sin∠OCE=0.6,sin∠CAD=sin∠COE=0.8; (2)弧CD的长=eq \f(106×3.14×10,180)≈18.5cm.
(1)在Rt△BCD中,CD=BCsin12°≈10×0.21=2.1(米).答:坡高2.1米; (2)在Rt△BCD中,BD=BCcs12°≈10×0.98=9.8(米).在Rt△ACD中,AD=eq \f(CD,tan5°)≈eq \f(2.1,0.09)≈23.33(米),∴AB=AD-BD≈23.33-9.8=13.53≈13.5(米).答:斜坡新起点与原起点的距离为13.5米.
11.eq \f(1,2)mnsinθ
第12题图
12设EF与AB交点为G,在Rt△BEG中,∵∠EGB=∠AGF=60°,∴EG=eq \f(BE,sin60°)=2,GB=eq \f(1,2)EG=1,在Rt△AGF中,GF=AG·sin30°=2×eq \f(1,2)=1,∴EF=EG+GF=2+1=3(m).
13.如图,延长CE交AB于F,∵α=30°,DE=2m,BD=8m,∴EF=BD+DEcs30°=8+2×eq \f(\r(3),2)=(8+eq \r(3))m,点E到底面的距离=DEsin30°=2×eq \f(1,2)=1m,即BF=1m,∴CF=EF+CE=8+eq \r(3)+1=(9+eq \r(3))m,根据同时同地物高与影长成正比得,eq \f(AF,CF)=eq \f(1,2),∴AF=eq \f(1,2)CF=eq \f(1,2)(9+eq \r(3))=eq \f(1,2)×10.73≈5.4m,∴树AB的高为5.4+1=6.4m.
第13题图
14.∵∠BAD=∠AFG=18°,∴在Rt△ABD中,eq \f(BD,AB)=tan18°,∴BD=AB·tan18°=9×tan18°≈2.9(m).∵BC=0.5m,∴CD=2.9-0.5=2.4(m).在Rt△CED中,∠DCE=18°,∴eq \f(CE,CD)=cs18°.∴CE=CD·cs18°=2.4×cs18°≈2.3(m).答:CE长约为2.3m.
浙教版九年级下册1.3 解直角三角形精品综合训练题: 这是一份浙教版九年级下册1.3 解直角三角形精品综合训练题,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中第一章 解直角三角形1.3 解直角三角形测试题: 这是一份初中第一章 解直角三角形1.3 解直角三角形测试题,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙教版九年级下册第一章 解直角三角形1.3 解直角三角形当堂达标检测题: 这是一份浙教版九年级下册第一章 解直角三角形1.3 解直角三角形当堂达标检测题,共20页。试卷主要包含了0分),【答案】B,【答案】A等内容,欢迎下载使用。













