初中冀教版21.1 一次函数学案及答案
展开21.1 一次函数
学习要求
知识与技能目标:
1.理解一次函数、正比例函数的概念.
2.根据实际问题列出简单的一次函数的表达式.
过程与方法目标:
经历由实际问题引出一次函数解析式的过程,体会数学与现实生活的联系.
情感态度与价值观:
探求一次函数解析式的求法,发展学生的数学应用能力培养学的应用数学的能力.
重点难点
1.正比例函数
【剖析】
一般地,形如y=kx(k是常数且k≠0)的函数,叫做正比例函数,其中k叫比例系数.
2. 一次函数
【剖析】
(1)一般地,形如y=kx+b(k,b是常数,且k≠0)的函数,叫做一次函数.
(2)当b=0时, y=kx+b即为y=kx,所以说正比例函数是特殊的一次函数.
回顾与思考
1.什么叫函数?
2.函数有哪些表达方式?
议一议
在现实生活当中有许多问题都可以归结为函数问题,大家能不能举一些例子?
做一做
1. 某弹簧的自然长度为3 cm,在弹性限度内,所挂物体的质量x每增加1千克,弹簧长度y增加0.5 cm.
(1) 计算所挂物体的质量分别为 1 kg, 2 kg, 3 kg, 4 kg, 5 kg时的长度,并填入下表:
(2)你能写出x与y之间的关系吗?
做一做
2.某辆汽车油箱中原有油100 L,汽车每行驶50 km耗油9 L.
(1) 完成下表:
(2) 你能写出x与y的关系吗?
议一议
(3) 汽车行驶的路程x可以无限增大吗?
行驶路程有没有一个取值范围?
油箱剩余油量y呢?
上面的两个函数关系式: (1)y=3+0.5x
(2) y=100-0.18x,大家讨论一下,这两个函数关系式有什么关系吗?请小组间交流.
一次函数:
若两个变量 x、y之间的关系可以表示成y=kx+b(b为常数,k不等于0)的形式,则称 y是x的一次函数.(x为自变量,y为因变量.)
当b=0时,称y是x的正比例函数
练一练
1.在函数(1)y = 3/x,(2)y=x-5, (3) y=-4x,
(4) y=2x -3x, (5) y=√x-2, (6) y= 1/x-2 中
是一次函数的是 ,是正比例函数的是
2.若函数 y=(6+3m)x+4n-4是一次函数,
则m,n应该满足的条件是 ,若是正比例函数,则m,n应该满足是 .
3.当k= 时,函数y=(k+3)x k2-8 -5是关于x的一次函数 .
例1 写出下列各题中y与 x之间的关系式,并判断:y是否为x的一次函数?是否为正比例函数?
(1)汽车以60km/h的速度匀速行驶,行驶路程为y(km)与行驶时间x(h)之间的关系;
(2)圆的面积y (cm2 )与它的半径x (cm)之间的关系.
(3)一棵树现在高5 0 cm,每个月长高2 cm,x 月后这棵树的高度为y cm.
例2 某地区电话的月租费为25元,在此基础上,可免费打50次市话(每次3分钟),超过50次后,每次0.2元.
(1)写出每月电话费y(元)与通话次数x(x>50)的函数关系式;
(2)求出月通话150次的电话费;
(3)如果某月通话费为53.6元,求该月通话的次数.
练一练
下列语句中,具有正比例函数关系的是( ).
A.长方形花坛的面积不变, 长y与宽 x 之间的关系;
B.正方形的周长不变, 边长 x与面积 S 之间的关系;
C.三角形的一条边不变, 这条边上的高h与S之间的关系;
D.圆的面积为S , 半径为r , S 与r 之间的关系.
2. 如图,在△ABC中, ∠B与∠C 的平分线交于点P, 设∠A=x, ∠BPC=y, 当∠A变化时,求y与x之间的函数关系式,并判断y是不是x的一次函数.
注:一次函数: 若两个变量 x、y之间的关系可以表示成y=kx+b(b为常数,k不等于0)的形式,则称 y是x的一次函数.(x为自变量,y为因变量.)
当b=0时,称y是x的正比例函数.
x/kg
0
1
2
3
4
5
y/cm
汽车行使路程x/km
0
50
100
150
200
300
油箱剩余油量y/L
数学21.4 一次函数的应用第1课时导学案及答案: 这是一份数学21.4 一次函数的应用第1课时导学案及答案,共3页。学案主要包含了学习设计反思等内容,欢迎下载使用。
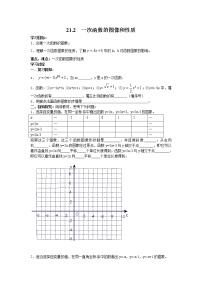
初中数学冀教版八年级下册21.2 一次函数的图像和性质导学案及答案: 这是一份初中数学冀教版八年级下册21.2 一次函数的图像和性质导学案及答案,共2页。学案主要包含了新知探究,新知归纳,课堂练习,课后反思等内容,欢迎下载使用。
数学21.3 用待定系数法确定一次函数表达式学案: 这是一份数学21.3 用待定系数法确定一次函数表达式学案,共2页。学案主要包含了复习,方法总结,课堂作业,课后反思等内容,欢迎下载使用。