四年级思维专项训练16 其他方法求面积(试卷+解析)

四年级思维训练16 其他方法求面积

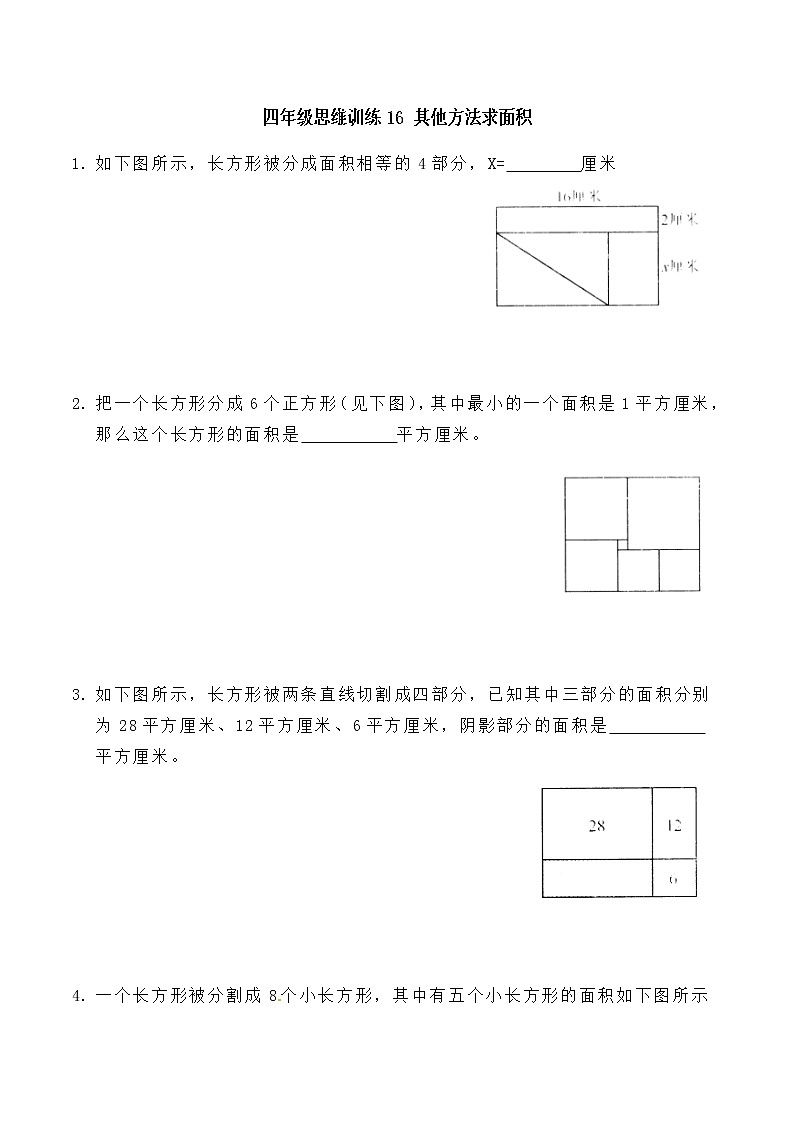
1. 如下图所示，长方形被分成面积相等的4部分，X=       厘米

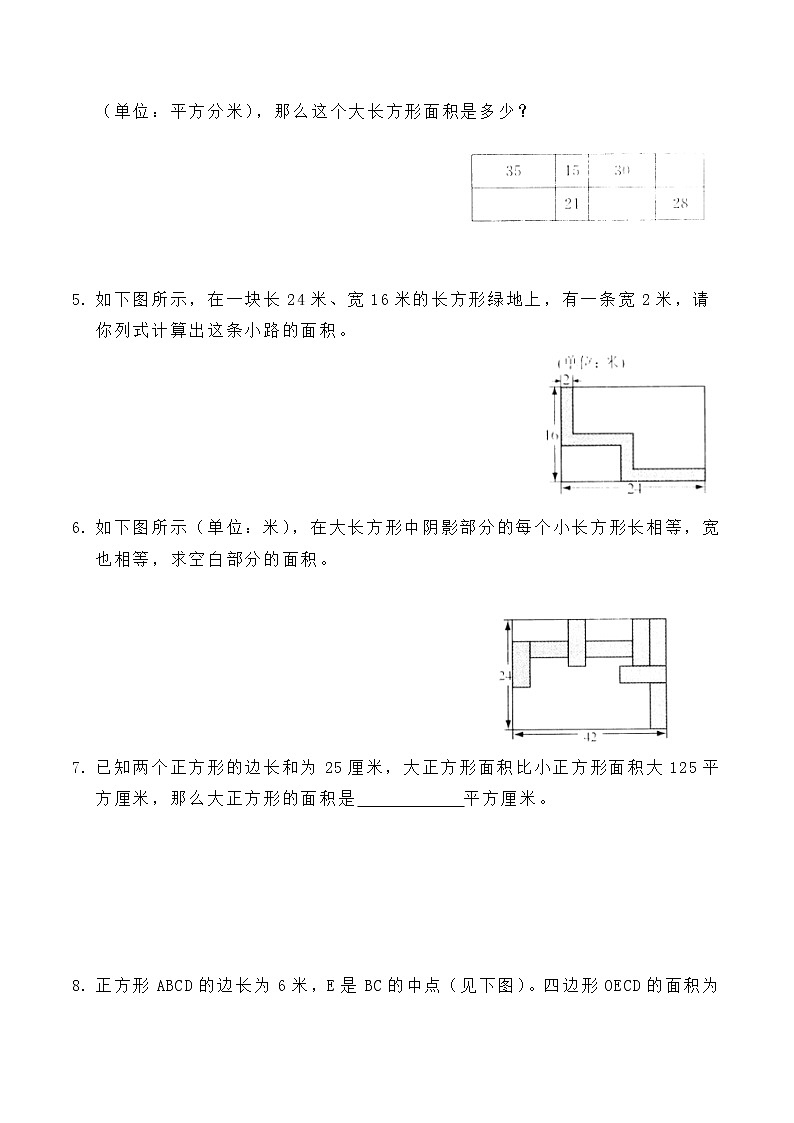
2. 把一个长方形分成6个正方形（见下图），其中最小的一个面积是1平方厘米，那么这个长方形的面积是         平方厘米。

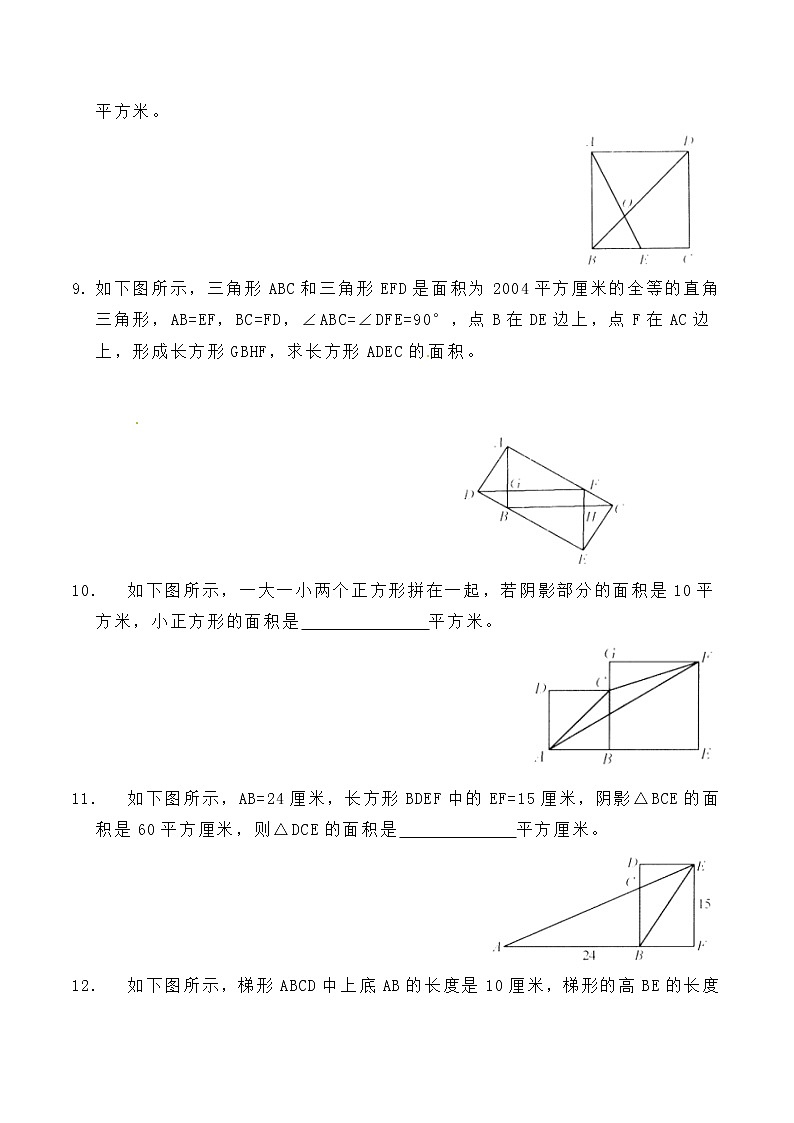
3. 如下图所示，长方形被两条直线切割成四部分，已知其中三部分的面积分别为28平方厘米、12平方厘米、6平方厘米，阴影部分的面积是         平方厘米。

4. 一个长方形被分割成8个小长方形，其中有五个小长方形的面积如下图所示（单位：平方分米），那么这个大长方形面积是多少？

5. 如下图所示，在一块长24米、宽16米的长方形绿地上，有一条宽2米，请你列式计算出这条小路的面积。

6. 如下图所示（单位：米），在大长方形中阴影部分的每个小长方形长相等，宽也相等，求空白部分的面积。

7. 已知两个正方形的边长和为25厘米，大正方形面积比小正方形面积大125平方厘米，那么大正方形的面积是          平方厘米。

8. 正方形ABCD的边长为6米，E是BC的中点（见下图）。四边形OECD的面积为  平方米。

9. 如下图所示，三角形ABC和三角形EFD是面积为2004平方厘米的全等的直角三角形，AB=EF，BC=FD，∠ABC=∠DFE=90°，点B在DE边上，点F在AC边上，形成长方形GBHF，求长方形ADEC的面积。

10. 如下图所示，一大一小两个正方形拼在一起，若阴影部分的面积是10平方米，小正方形的面积是            平方米。

11. 如下图所示，AB=24厘米，长方形BDEF中的EF=15厘米，阴影△BCE的面积是60平方厘米，则△DCE的面积是           平方厘米。

12. 如下图所示，梯形ABCD中上底AB的长度是10厘米，梯形的高BE的长度是12厘米，且E是CD中点，BF将梯形ABCD分成面积相等的两部分。那么，BF的长度是  厘米。

13. 如下图所示，ABCD是边长为18厘米的正方形，M、N分别是AB边上的点，已知：AM=2MB，CN=2NB,AN与CM相交于点O，则四边形AOCD的面积是        平方厘米。

[

14. 如下图所示，甲乙丙三个正方形，它们的边长分别是4厘米、6厘米、8厘米。乙的一个顶点在甲的中心点上，丙的一个顶点在乙的中心点上，并且甲和丙没有交集。这三个正方形的覆盖面积是多少？

15. 校园里有一块长方形的地，长18米，宽12米，想种上红花、黄花和绿草。一种设计方案如下图，（除长方形四个顶点外，其余各点均为各边中点）那么其中红花的面积是          平方米。

16. 如下图所示，5×5的方格中，每个小方格的边长为1，A、B两点在小方格的顶点上。现在要在小方格的顶点上确定一点C，连接AC、BC后，使得三角形ABC的面积最大，请在图中标出C点，并求出最大面积为多少？

17. 用1、2、3、4、5、6、7、8这8个数作为下图图形的八条边的边长（单位：米），不同的组成有不同的面积，那么这个图形的最大面积是多少？

18. 如下图所示，有ABCD四块大小一样的正方形纸片，放在一个大正方形纸盒中它们之间互相叠合，已知露在外面的部分中，A的面积为144平方厘米，B的面积是96平方厘米，D的面积是84平方厘米，那么C露出部分的面积是        平方厘米。

19. 桌面上放有四张大小不同的正方形纸片，边长分别为2米、3米、4米、5米。若分别取走边长为2米、3米、4米、5米的正方形纸片中的一个，则剩下的三张纸片覆盖的面积分别减少2平方米、3平方米、4平方米、5平方米。那么四张纸片覆盖的面积为          平方米。

四年级思维训练16 其他方法求面积

参考答案

1. 如下图所示，长方形被分成面积相等的4部分，X=       厘米．

【答案】6

【分析】长为1 6，宽为ⅹ的长方形面积等于上面1 6×2的长方形面积的3倍，所以ⅹ＝6厘米．

2. 把一个长方形分成6个正方形（见下图），其中最小的一个面积是1平方厘米，那么这个长方形的面积是         平方厘米。

【答案】1 4 3

【分析】如下图所示，由图②的面积与图③的面积相等，记⑥的边长为ａ，则⑤的边长为ａ一1，④的边长为ａ一2，③与②的边长均为ａ一3，所以⑥的边长比图②的边长多3厘米，因此图③的边长为3+1＝4（厘米），④的边长为4+1＝5（厘米），图⑤的边长为5+1＝6（厘米），图⑥的边长为6+1＝7（厘米）．所以长方形的长和宽分别为6+7=13（厘米），5+6 =11（厘米），所以长方形的面积为1 3×11=143（平方厘米）．

（１）

3. 如下图所示，长方形被两条直线切割成四部分，已知其中三部分的面积分别为28平方厘米、12平方厘米、6平方厘米，阴影部分的面积是         平方厘米。

【答案】１４

【分析】长方形十字交叉相乘原理．如下图（２）所示，设分成的四个小长方形的边长为以、ａ、ｂ、c、d，左上角的长方形面积是ac，右上角的长方形面积是ad，左下角的长方形面积是ｂc，右下角的长方形面积是ｂd，所以不相邻的两个长方形面积的乘积相等，均为abcd．则有28×6=12×阴影部分面积，故阴影部分面积是28×6÷12=14．

（１）　　　　　　（２）

4. 一个长方形被分割成8个小长方形，其中有五个小长方形的面积如下图所示（单位：平方分米），那么这个大长方形面积是多少？

【答案】２４０

【分析】根据十字交叉相乘原理，三个空白部分面积分别是35×21÷15=49，30×21÷15 =42，30×2 8÷42=20，总面积=35+15+30+20+49+21+42+28=240（平方分米）．

5. 如下图所示，在一块长24米、宽16米的长方形绿地上，有一条宽2米，请你列式计算出这条小路的面积。

【答案】７６

【分析】阴影部分即小路的面积等于路宽乘以路长，路宽为2，路长为长方形的长加宽再减去路宽，可按上图将小路等积变形，其面积为2×24+2×16-2×2=76（平方米）．

（１）　　　　　　（２）

6. 如下图所示（单位：米），在大长方形中阴影部分的每个小长方形长相等，宽也相等，求空白部分的面积。

【答案】５７６平方米

【分析】观察图形，可以得到长方形的长宽关系满足：

，解之得

所以空白部分的面积为2 4×42—8×9×6=576（平方米）．

7. 已知两个正方形的边长和为25厘米，大正方形面积比小正方形面积大125平方厘米，那么大正方形的面积是          平方厘米。

【答案】225

【分析】如下图所示，它是非常典型的两个正方形模型的分析方法．两个正方形之间的环形部分可以分成4个完全相同的长方形，不妨设它们的宽是a厘米．长是b厘米，那么大正方形的边长是（a+b）厘米，小正方形的边长是（b—a）厘米．

所以大正方形的面积是(1 2.5+2.5)×(12. 5+2.5)=225（平方厘米）．

8. 正方形ABCD的边长为6米，E是BC的中点（见下图）。四边形OECD的面积为  平方米。

【答案】15

【分析】如下图所示，连接DE，根据等积变形，设S△BEO=1份，那么S△ABO=S△DEO=2份，S△ADO=4份，所以S△DCE=S△DBE=3份，正方形ABCD共为1+2+2+4+3=12(份)，

四边形0ECD的面积为6×6÷1 2×(2+3)=1 5（平方米）．

(1)                (2)

9. 如下图所示，三角形ABC和三角形EFD是面积为2004平方厘米的全等的直角三角形，AB=EF，BC=FD，∠ABC=∠DFE=90°，点B在DE边上，点F在AC边上，形成长方形GBHF，求长方形ADEC的面积。

【答案】4 008平方厘米

【分析】如下图所示，连接BF，因为三角形ADB的面积等于三角形BDF的面积，同时减去三角形BDG的面积，可得三角形ADG的面积与三角形BGF的面积相等，三角形CEH的面积与三角形BHF的面积相等，所以长方形ADEC的面积为三角形ABC面积的2倍，为4008平方厘米，也可以利用一半模型得出结论．

(1)            (2)

10. 如下图所示，一大一小两个正方形拼在一起，若阴影部分的面积是10平方米，小正方形的面积是            平方米。

【答案】20

【分析】如下图所示，连接BF,BF和AC平行，阴影部分面积等于三角形ABC的面积，而三角形ABC的面积是小正方形面积的一半，所以小正方形的面积是阴影部分面积的2倍，为20平方米.

(1)             (2)

11. 如下图所示，AB=24厘米，长方形BDEF中的EF=15厘米，阴影△BCE的面积是60平方厘米，则△DCE的面积是           平方厘米。

【答案】30

【分析】如下图所示，连接AD，则三角形BCE的面积等于三角形ACD的面积，所以CD=60×2÷24=5（厘米），CB=15—5=10（厘米），又因为三角形DCE和三角形BCE同高，且CB是CD的2倍，所以三角形BCE的面积是三角形DCE面积的2倍，所以三角形DCE的面积是6 0÷2=30（平方厘米）．

(1)            (2)

12. 如下图所示，梯形ABCD中上底AB的长度是10厘米，梯形的高BE的长度是12厘米，且E是CD中点，BF将梯形ABCD分成面积相等的两部分。那么，BF的长度是  厘米。

【答案】13

【分析】见下图，取AB中点G，连接GE，因为E是CD中点，所以GE将梯形ABCD分成面积相等的两部分，又因为BF将梯形ABCD分成面积相等的两部分，所以三角形BOG和三角形EOF的面积相等，所以EF= BG=5厘米，由勾股定理，=169，所以BF=13厘米．

(1)     (2)

13. 如下图所示，ABCD是边长为18厘米的正方形，M、N分别是AB边上的点，已知：AM=2MB，CN=2NB,AN与CM相交于点O，则四边形AOCD的面积是        平方厘米。

【答案】243

【分析】如下图(2)所示，连接OB，由AM=2MB，CN=2NB，

有：S△AMO=2S△BMO且S△CNO=2S△BNO

又S△ABN=S△CBM= 18×6÷2=54(平方厘米)，

所以S△AMO= S△CNO=2S△BMO=2S△BNO=54÷4×2=27（平方厘米）

那么S△AOCD=1 8×18-54-27=243(平方厘米)．

(1)              (2)

14. 如下图所示，甲乙丙三个正方形，它们的边长分别是4厘米、6厘米、8厘米。乙的一个顶点在甲的中心点上，丙的一个顶点在乙的中心点上，并且甲和丙没有交集。这三个正方形的覆盖面积是多少？

【答案】103平方厘米

【分析】甲的面积是1 6平方厘米，乙的面积是3 6平方厘米，丙的面积是6 4平方厘米，甲和乙的重合部分，是从甲的中心做一个9 0°的角，甲乙重叠的面积是甲的面积的；同样的，乙和丙的重合部分的面积是乙的面积的，实际上，我们可以旋转甲和乙，如下图（2）所示：那么覆盖的面积是16+36+64-4- 9=103（平方厘米）．

（1）                 （2）

15. 校园里有一块长方形的地，长18米，宽12米，想种上红花、黄花和绿草。一种设计方案如下图，（除长方形四个顶点外，其余各点均为各边中点）那么其中红花的面积是          平方米。

【答案】54平方米

【分析】图中黄花面积十红花面积=长方形面积的一半，而且黄花面积=红花面积，所以，红花面积=18×12÷2÷2=54（平方米）．

16. 如下图所示，5×5的方格中，每个小方格的边长为1，A、B两点在小方格的顶点上。现在要在小方格的顶点上确定一点C，连接AC、BC后，使得三角形ABC的面积最大，请在图中标出C点，并求出最大面积为多少？

【答案】4平方米

【分析】要使三角形ABC的面积尽可能大，因为AB长度同定，那么就是要求A B边上的高尽可能大，显然当另外一个点在C或D时这个高是最大的。

对于C：S△ABC=SEFGC一S△AEC一S△ABF -S△GBC=3×4-3×2÷2—2×1÷2-2×4÷2—4（平方米），

对于D：同理有S△ABD=3×3-3×2÷2-3×1÷2-2×1÷2=3.5（平方米），

所以所求C点如下图所示，且这个最大面积是4平方米．

(1)             (2)

17. 用1、2、3、4、5、6、7、8这8个数作为下图图形的八条边的边长（单位：米），不同的组成有不同的面积，那么这个图形的最大面积是多少？

【答案】50

【分析】首先肯定有a+b+c=d．

要使图形的面积最大，那么d×h要最大，那么是7×8；阴影部分的面积要最小，即a×(g一f)+b×g最小，那么g一f=1，a和b取2和1．

最后组成如下右图所示的图形，面积是7×8一[2×(4-3)+1×4]=50．

18. 如下图所示，有ABCD四块大小一样的正方形纸片，放在一个大正方形纸盒中它们之间互相叠合，已知露在外面的部分中，A的面积为144平方厘米，B的面积是96平方厘米，D的面积是84平方厘米，那么C露出部分的面积是        平方厘米。

【答案】46.25

【分析】首先向左移动正方形B，使它有两边与大正方形的边重合，如下图1所示．

此时正方形B与正方形D露出部分的面积相等，均为(96+84)÷2=90（平方厘米）．所以图1中正方形C露出的面积为90×90÷144=56. 25（平方厘米）．再计算图2中正方形B小E这部分．H部分的面积是90-84=6（平方厘米），E、F两部分的面积和是90，故G、H两部分的面积和是144—90=54（平方厘米）．E部分的面积是90÷(54÷6)=10（平方厘米）．故C露出部分的面积为56. 25-10=46. 25（平方厘米）．

19. 桌面上放有四张大小不同的正方形纸片，边长分别为2米、3米、4米、5米。若分别取走边长为2米、3米、4米、5米的正方形纸片中的一个，则剩下的三张纸片覆盖的面积分别减少2平方米、3平方米、4平方米、5平方米。那么四张纸片覆盖的面积为          平方米。

【答案】34

【分析】方法一：四张纸片的面积分别为4平方米，9平方米，1 6平方米，2 5平方米；每张纸片与其他纸片重叠部分的面积分别为4-2=2（平方米），9-3=6（平方米），16-4=12（平方米），25-5=20（平方米），由于2+6+12=20（平方米），所以只能前3张纸片与第4张分别重叠，没有三张重叠在一起的部分，重叠部分的面积为2 0平方米，所以总的覆盖面积为4+9+16--25-20=34（平方米）．

下图给出一种重叠方式：

方法二：因为若分别取走边长为2米、3米、4米的正方形纸片，剩下的三张纸片覆盖的面积分别减少2平方米、3平方米、4平方米．所以边长为5米的正方形纸片中和其余纸片重叠部分的面积和最多为(2×2—2)+(3×3—3)+(4×4—4)一2 0（平方米），

而又因为去掉边长为5米的正方形纸片则剩下的三张纸片覆盖的面积少了5平方米，所以边长为5米的正方形纸片和其余纸片重叠部分的面积最少为2 0平方米．那么重叠部分面积就是2 0平方米，所以四张纸片覆盖的面积为25+2+3+4=3 4（平方米）．