2021版新高考地区高考数学（人教版）大一轮复习（课件+学案）第11章 阅读与欣赏(九)　概率、统计综合问题的三种常用求解策略

概率、统计综合问题的三种常用求解策略

策略一　公式法

在某校教师趣味投篮比赛中，比赛规则是：每场投6个球，至少投进4个球且最后2个球都投进者获奖；否则不获奖．已知教师甲投进每个球的概率都是.

(1)记教师甲在每场的6次投球中投进球的个数为X，求X的分布列；

(2)求教师甲在一场比赛中获奖的概率．

【解】　(1)X的所有可能取值为0，1，2，3，4，5，6.

依条件可知，X～B(6，)，

P(X＝k)＝C·()k·()6－k(k＝0，1，2，3，4，5，6)．

所以X的分布列为

(2)设教师甲在一场比赛中获奖为事件A，

则P(A)＝C·()2·()4＋C··()5＋()6＝，即教师甲在一场比赛中获奖的概率为.

对于此类问题求解，若随机变量X服从二项分布B(n，p)，则其概率、均值与方差可直接利用公式P(X＝k)＝Cpk(1－p)n－k(k＝0，1，2，…，n)，E(X)＝np，D(X)＝np(1－p)求得．　

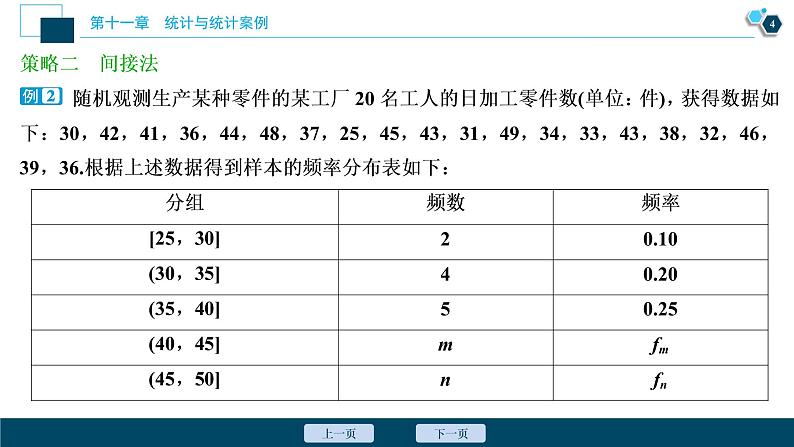
策略二　间接法

随机观测生产某种零件的某工厂20名工人的日加工零件数(单位：件)，获得数据如下：30，42，41，36，44，48，37，25，45，43，31，49，34，33，43，38，32，46，39，36.根据上述数据得到样本的频率分布表如下：

(1)确定样本频率分布表中m，n，fm和fn的值；

(2)根据上述频率分布表，画出样本频率分布直方图；

(3)根据样本频率分布直方图，求在该厂任取3人，至少有1人的日加工零件数落在区间(30，35]内的概率．

【解】　(1)由已知数据，得区间(40，45]内的频数m＝6，区间(45，50]内的频数n＝3，故fm＝＝0.3，fn＝＝0.15.

(2)由频率分布表，画出频率分布直方图如下图：

(3)根据样本频率分布直方图，每人的日加工零件数落在区间(30，35]内的频率为0.2，设所取的3人中，日加工零件数落在区间(30，35]内的人数为ξ，则ξ～B(3，0.2)，

故P(ξ≥1)＝1－P(ξ＝0)＝1－(1－0.2)3＝0.488.

因此至少有1人的日加工零件数落在区间(30，35]内的概率为0.488.

当复杂事件正面情况比较多，反面情况较少时，可利用其对立事件进行求解，即“正难则反”．对于“至少”“至多”等问题往往用这种方法求解．　

策略三　对称法

从某企业生产的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：

(1)求这500件产品质量指标值的样本平均数和样本方差s2(同一组中的数据用该区间的中点值作代表)；

(2)由直方图可以认为，这种产品的质量指标值Z服从正态分布N(μ，σ2)，其中μ近似为样本平均数，σ2近似为样本方差s2.

①利用该正态分布，求P(187.8＜Z＜212.2)；

②某用户从该企业购买了100件这种产品，记X表示这100件产品中质量指标值位于区间(187.8，212.2)的产品件数．利用①的结果，求EX.

附：≈12.2.

若Z～N(μ，σ2)，则P(μ－σ＜Z＜μ＋σ)＝0.682 7，P(μ－2σ＜Z＜μ＋2σ)＝0.954 5.

【解】　(1)抽取产品的质量指标值的样本平均数和样本方差s2分别为＝170×0.02＋180×0.09＋190×0.22＋200×0.33＋210×0.24＋220×0.08＋230×0.02＝200，

s2＝(－30)2×0.02＋(－20)2×0.09＋(－10)2×0.22＋0×0.33＋102×0.24＋202×0.08＋302×0.02＝150.

(2)①由(1)知，Z～N(200，150)，

从而P(187.8＜Z＜212.2)＝P(200－12.2＜Z＜200＋12.2)＝0.682 7.

②由①知，一件产品的质量指标值位于区间(187.8，212.2)的概率为0.682 7，

依题意知X～B(100，0.682 7)，

所以EX＝100×0.682 7＝68.27.

解决与正态分布有关的问题，在理解μ，σ2的意义情况下，记清正态分布的密度曲线是一条关于μ对称的钟形曲线，很多问题都是利用图象的对称性解决的．