初中数学人教版八年级上册14.2 乘法公式综合与测试优秀课时训练

这是一份初中数学人教版八年级上册14.2 乘法公式综合与测试优秀课时训练，共7页。试卷主要包含了2 乘法公式 课时训练，5×200，5）×＝40000﹣0等内容，欢迎下载使用。

一．选择题


1．下列各式中，能用平方差公式计算的是（ ）


A．（p+q）（p+q） B．（p﹣q）（p﹣q） C．（p+q）（p﹣q） D．（p+q）（﹣p﹣q）


2．若（2a+3b）（ ）＝9b2﹣4a2，则括号内应填的代数式是（ ）


A．﹣2a﹣3bB．2a+3bC．2a﹣3bD．3b﹣2a


3．计算（x+3y）2﹣（x﹣3y）2的结果是（ ）


A．12xyB．﹣12xyC．6xyD．﹣6xy


4．若多项式x2+kx+9是一个完全平方式，则常数k的值是（ ）


A．6B．3C．±6D．±3


5．计算（x+1）（x﹣1）（x2+1）的结果是（ ）


A．x2﹣1B．x3﹣1C．x4+1D．x4﹣1


6．已知a+b＝5，ab＝3，则a2+b2＝（ ）


A．25B．22C．19D．13


7．如图，两个正方形边长分别为a、b，且满足a+b＝10，ab＝12，图中阴影部分的面积为（ ）





A．100B．32C．144D．36


8．如图，从边长为m的大正方形中剪掉一个边长为n的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是（ ）





A．（m﹣n）2＝m2﹣2mn+n2B．m2﹣n2＝（m+n）（m﹣n）


C．（m﹣n）2＝m2﹣n2D．m（m﹣n）＝m2﹣mn


二．填空题


9．x2﹣4x+k是完全平方式，则k＝ ．


10．（2x+3y）2＝ ；（2a﹣b）（﹣b﹣2a）＝ ．


11．若x2+y2＝10，xy＝3，则（x﹣y）2＝ ．


12．如果（2x+2y+1）（2x+2y﹣1）＝15，那么x+y的值是 ．


13．已知a+＝3，则a2+的值是 ．


14．计算：12（1+72）（1+74）（1+78）（1+716）的结果为 ．


三．解答题


15．计算：9（x﹣2）2﹣（3x+2）（3x﹣2）











16．199.5×200.5（运用公式简便运算）














17．先化简，再求值：（a+3）2﹣（a+1）（a﹣1）﹣2（2a+4），其中a＝．














18．已知x+y＝4，xy＝3，求下列各式的值：


（1）2x2y+2xy2；


（2）x﹣y




















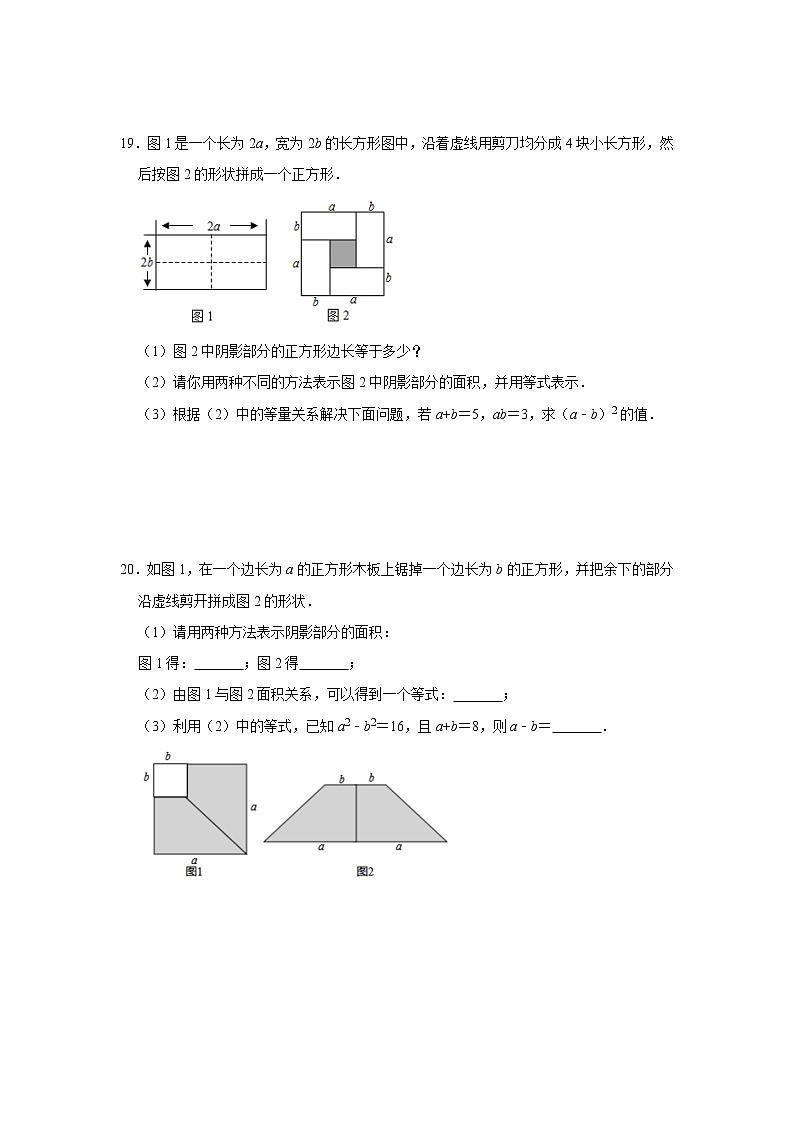
19．图1是一个长为2a，宽为2b的长方形图中，沿着虚线用剪刀均分成4块小长方形，然后按图2的形状拼成一个正方形．





（1）图2中阴影部分的正方形边长等于多少？


（2）请你用两种不同的方法表示图2中阴影部分的面积，并用等式表示．


（3）根据（2）中的等量关系解决下面问题，若a+b＝5，ab＝3，求（a﹣b）2的值．














20．如图1，在一个边长为a的正方形木板上锯掉一个边长为b的正方形，并把余下的部分沿虚线剪开拼成图2的形状．


（1）请用两种方法表示阴影部分的面积：


图1得： ；图2得 ；


（2）由图1与图2面积关系，可以得到一个等式： ；


（3）利用（2）中的等式，已知a2﹣b2＝16，且a+b＝8，则a﹣b＝ ．




















参考答案


一．选择题


1．解：（p+q）（p+q）＝（p+q）2＝p2+2pq+q2；


（p﹣q）（p﹣q）＝（p﹣q）2＝p2﹣2pq+q2；


（p+q）（p﹣q）＝p2﹣q2；


（p+q）（﹣p﹣q）＝﹣（p+q）2＝﹣p2﹣2pq﹣q2．


故选：C．


2．解：∵（2a+3b）（3b﹣2a）＝9b2﹣4a2


即（3b+2a）（3b﹣2a）＝（3b）2﹣（2a）2


∴括号内应填的代数式是3b﹣2a．


故选：D．


3．解：原式＝x2+6xy+9y2﹣（x2﹣6xy+9y2）


＝x2+6xy+9y2﹣x2+6xy﹣9y2


＝12xy．


故选：A．


4．解：∵a2+ka+9＝a2+ka+32，


∴ka＝±2×a×3，


解得k＝±6．


故选：C．


5．解：原式＝（x2﹣1）（x2+1）


＝x4﹣1．


故选：D．


6．解：∵（a+b）2＝a2+2ab+b2，


∴a2+b2＝（a+b）2﹣2ab＝25﹣2×3＝19，


故选：C．


7．解：S阴影＝a2+b2﹣a2﹣（a+b）•b，


＝a2﹣ab+b2，


＝（a2﹣ab+b2），


＝[（a+b）2﹣3ab]，


当a+b＝10，ab＝12时，


原式＝（100﹣36）＝32．


故选：B．


8．解：左边图形的阴影部分可表示为：m2﹣n2


右边图形可表示为：（m﹣n）（m+n）


由于阴影部分面积相等，故m2﹣n2＝（m+n）（m﹣n），


故选：B．


二．填空题


9．解：∵x2﹣4x+k是完全平方式，


∴k＝22＝4，


故答案为：4


10．解：（2x+3y）2＝（2x）2+2•2x•3y+（3y）2＝4x2+12xy+9y2；


（2a﹣b）（﹣b﹣2a）＝（﹣b+2a）（﹣b﹣2a）＝b2﹣4a2．


故答案为：4x2+12xy+9y2，b2﹣4a2．


11．解：∵x2+y2＝10，xy＝3，


∴（x﹣y）2＝x2﹣2xy+y2＝x2+y2﹣2xy＝10﹣6＝4，


故答案为：4．


12．解：（2x+2y+1）（2x+2y﹣1）＝15，


（2x+2y）2﹣12＝15，


（2x+2y）2＝16，


2x+2y＝±4，


x+y＝±2，


故答案为：±2．


13．解：∵a+＝3，


∴a2+2+＝9，


∴a2+＝9﹣2＝7．


故答案为：7．


14．解：原式＝×（1+72）（1+74）（1+78）（1+716）


＝×（1+74）（1+78）（1+716）


＝×（1+78）（1+716）


＝（1+716）


＝．


故答案为：．


三．解答题


15．解：原式＝9（x2﹣4x+4）﹣（9x2﹣4）


＝9x2﹣36x+36﹣9x2+4


＝﹣36x+40．


16．解：原式＝（200﹣0.5）×（200+0.5）＝40000﹣0.25＝39999.75．


17．解：原式＝a2+6a+9﹣（a2﹣1）﹣4a﹣8


＝2a+2，


∵a＝，


∴原式＝1+2＝3．


18．解：（1）∵x+y＝4，xy＝3，


∴2x2y+2xy2＝2xy（x+y）＝2×4×3＝24；


（2）∵x+y＝4，xy＝3，


∴（x﹣y）2＝（x+y）2﹣4xy＝42﹣4×3＝4．


∴．


19．解：（1）根据拼图可知，阴影正方形的边长为（a﹣b），


（2）阴影正方形的边长为（a﹣b），因此S阴影正方形的面积＝（a﹣b）2，


S阴影正方形的面积＝S大正方形的面积﹣S图1的面积＝（a+b）2﹣4ab，


故有（a﹣b）2＝（a+b）2﹣4ab；


（3）由（2）得（a﹣b）2＝（a+b）2﹣4ab，


当a+b＝5，ab＝3时，（a﹣b）2＝（a+b）2﹣4ab＝52﹣4×3＝25﹣12＝13．


即（a﹣b）2的值为13．


20．解：（1）图1中阴影部分的面积为：a2﹣b2，


图2中阴影部分的面积为：（2b+2a）（a﹣b），即（a+b）（a﹣b）；


故答案为：a2﹣b2，（a+b）（a﹣b）；


（2）由图1与图2面积关系，可以得到一个等式：a2﹣b2＝（a+b）（a﹣b），


故答案为：a2﹣b2＝（a+b）（a﹣b）；


（3）∵a2﹣b2＝16，且a+b＝8，


∴（a+b）（a﹣b）＝16，


即8（a﹣b）＝16，


∴a﹣b＝2．


故答案为：2．