

初中数学人教版九年级上册第二十三章 旋转综合与测试优秀测试题
展开《23.1图形的旋转》
一、单选题
1.如图,将△ABC旋转至△CDE,则下列结论中一定成立的是( )
A.ACCEB.ADECC.ABCDD.BCEC
2.如图,将绕点逆时针旋转70°到的位置,若,则( )
A.45°B.40°C.35°D.30°
3.把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A.30°B.90°C.120°D.180°
4.如图,在平面直角坐标系中,将点绕原点顺时针旋转90°得到点,则的坐标为( )
A.B.C.D.
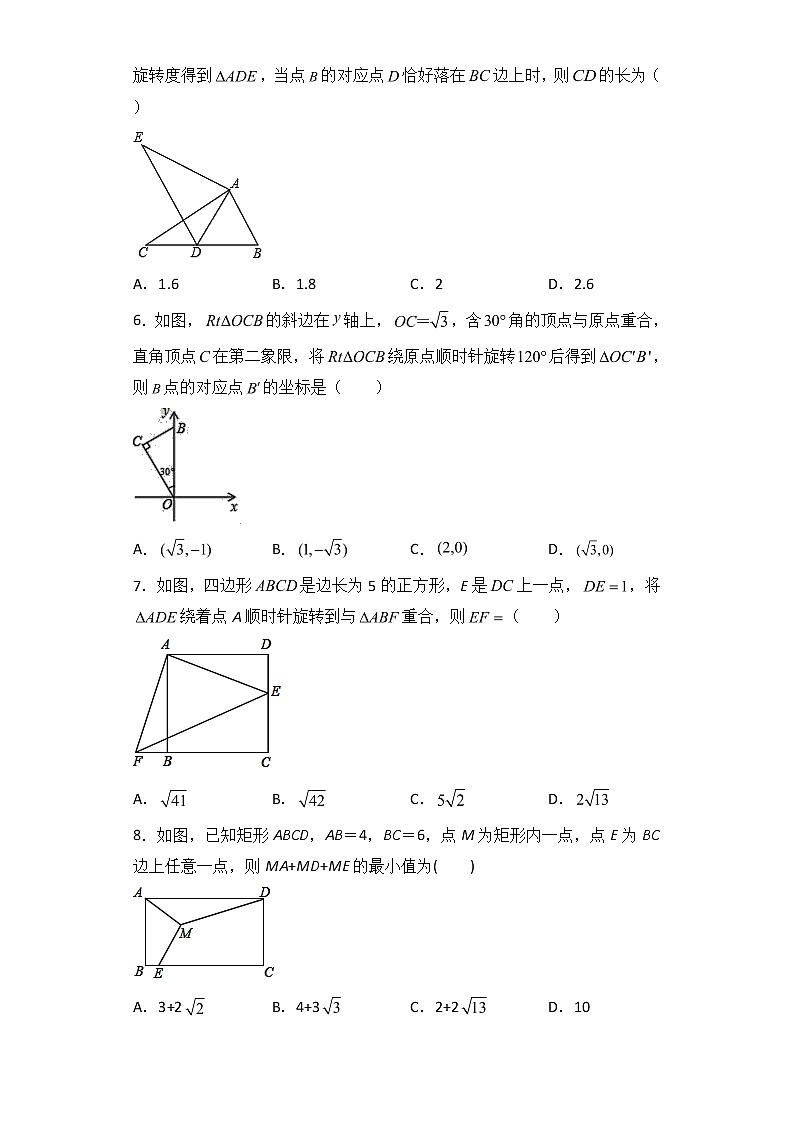
5.如图,在中,,,,将绕点顺时针旋转度得到,当点的对应点恰好落在边上时,则的长为( )
A.1.6B.1.8C.2D.2.6
6.如图,的斜边在轴上,,含角的顶点与原点重合,直角顶点在第二象限,将绕原点顺时针旋转后得到,则点的对应点的坐标是( )
A.B.C.D.
7.如图,四边形是边长为5的正方形,E是上一点,,将绕着点A顺时针旋转到与重合,则( )
A.B.C.D.
8.如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为( )
A.3+2B.4+3C.2+2D.10
二、填空题
9.将边长为1的正方形绕点按顺时针方向旋转到的位置(如图),使得点落在对角线上,与相交于点,则=_________.(结果保留根号)
10.在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是____________..
11.如图,在平面直角坐标系中,的直角顶点的坐标为 ,点在轴正半轴上,且.将先绕点逆时针旋转,再向左平移3个单位,则变换后点的对应点的坐标为______.
12.如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为__________
13.一副三角板如图放置,将三角板ADE绕点A逆时针旋转,使得三角板ADE的一边所在的直线与BC垂直,则的度数为______.
14.如图,等边三角形ABC内有一点P,分別连结AP、BP、CP,若,,.则=_______.
三、解答题
15.如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移两个单位长度,点A的对应点为点,点B的对应点为点,请画出平移后的线段;
(2)将线段绕点按逆时针方向旋转,点的对应点为点,请画出旋转后的线段;
(3)连接、,求的面积.
16.如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D, AB=AD.
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
17.如图,直线与轴交于点,与轴交于点,将线段绕点顺时针旋转90°得到线段,反比例函数的图象经过点.
(1)求直线和反比例函数的解析式;
(2)已知点是反比例函数图象上的一个动点,求点到直线距离最短时的坐标.
18.如图,在中,,,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转得到线段CE,连结DE交BC于点F,连接BE.
求证:≌;
当时,求的度数.
19.(1)问题发现
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.
填空:线段AD,BE之间的关系为 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.
(3)解决问题
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.
答案
1.D 2.D 3.C 4.D 5.A 6.A 7.D 8.B
9. 10.90°
11. 12.
13.15°或60°. 14.
15.解(1)线段如图所示;
(2)线段如图所示;
(3).
16.解:(1)、∵∠BAC=∠DAE,AB=AD,∠B=∠D,∴△ABD≌△ADE.
(2)、∵△ABC≌△ADE, ∴AC与AE是一组对应边, ∴∠CAE的旋转角,
∵AE=AC,∠AEC=75°, ∴∠ACE=∠AEC=75°, ∴∠CAE=180°—75°—75°=30°
17.解:(1)将点,点,代入,
∴,
∴;
∵过点作轴,
∵线段绕点顺时针旋转90°得到线段,
∴≌(),
∴,,
∴,
∴,
∴;
(2)设与平行的直线,
联立,
∴,
当时,,此时点到直线距离最短;
∴;
18.解由题意可知:,,
,
,
,
,
在与中,
,
≌;
,,
,
由可知:,
,
,
.
19.解(1)结论:AD=BE,AD⊥BE.
理由:如图1中,
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,
∠ACB=∠ACD=90°,
在Rt△ACD和Rt△BCE中
∴△ACD≌△BCE(SAS),
∴AD=BE,∠EBC=∠CAD
延长BE交AD于点F,
∵BC⊥AD,
∴∠EBC+∠CEB=90°,
∵∠CEB=AEF,
∴∠EAD+∠AEF=90°,
∴∠AFE=90°,即AD⊥BE.
∴AD=BE,AD⊥BE.
故答案为AD=BE,AD⊥BE.
(2)结论:AD=BE,AD⊥BE.
理由:如图2中,设AD交BE于H,AD交BC于O.
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=90°,
∴ACD=∠BCE,
在Rt△ACD和Rt△BCE中
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE,
∵∠CAO+∠AOC=90°,∠AOC=∠BOH,
∴∠BOH+∠OBH=90°,
∴∠OHB=90°,
∴AD⊥BE,
∴AD=BE,AD⊥BE.
(3)如图3中,作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,
∴PC=BE,
图3-1中,当P、E、B共线时,BE最小,最小值=PB-PE=5-3,
图3-2中,当P、E、B共线时,BE最大,最大值=PB+PE=5+3,
∴5-3≤BE≤5+3,
即5-3≤PC≤5+3.
九年级数学上册 23. 2中心对称
基础闯关全练
1.下列图形中,△A'B'C'与△ABC成中心对称的是( )
A.
B.
C.
D.
2.如图23 -2-1-1,△ABC与△DEF成中心对称,则对称中心是( )
点C
B.点D
C.线段BC的中点
D.线段FC的中点
3.如图23-2-1-2,△ABC与△DEF关于点O成中心对称,则AB_______DE,BC//________,AC=______.
4.如图23-2-1-3,在方格网中,已知格点△ABC和点O.
(1)画△A'B'C'和△ABC关于点O成中心对称;
(2)请在方格网中标出所有使以点A、O、C'、D为顶点的四边形是平行四边形的D点.
能力提升全练
1.如图23 -2-1-4,△DEC是由△ABC经过了如下的几何变换而得到的:①以AC所在直线为对称轴作轴对称,再以C为旋转中心,顺时针旋转90°;②以C为旋转中心,顺时针旋转90°得△A'B'C,再以A'C所在直线为对称轴作轴对称;③将△ABC向下、向左各平移1个单位,再以AC的中点为中心作中心对称.其中正确的变换有( )
①②
①③
②③
D.①②③
2.如图23 -2-1-5所示,△AOD和△COB关于点O中心对称,∠AOD= 60°,∠ADO=90°,BD=12,点P是AO上一动点,点Q是OC上一动点(P,Q不与端点重合),且AP= OQ,连接BQ,DP,则DP+BQ的最小值是_________.
三年模拟全练
一、选择题
1.(2019四川自贡富顺期中,2,★☆☆)如图23-2-1-6,△ABC与△A'B'C'关于点O成中心对称,下列结论中不成立的是( )
OC = OC'
OA = OA '
BC=B'C'
∠ABC= ∠A'C'B'
二、填空题
2.(2018山东东营胜利一中期末,14,★☆☆)如图23-2-1-7,在△ABC中,点O是AC
的中点,△CDA与△ABC关于点O中心对称,若AB=6,∠BAC= 40º,则CD的长度为________,∠ACD的度数为_________.
三、解答题
3.△ABC在平面直角坐标系xOy中的位置如图23 -2 -1-8所示.
(1)作△ABC关于点C成中心对称的△A₁B₁C;
(2)写出点A₁、B₁的坐标.
解答题
如图23 -2 -1-9,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).
(1)作出△ABC关于原点O成中心对称的△A₁B₁C₁;
(2)作出点A关于x轴的对称点A ',若把点A'向右平移a个单位长度后落在△A₁B₁C₁的内部(不包括顶点和边界),求a的取值范围.
核心素养全练
1.(2018山东潍坊中考)在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图23-2-1-10,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径,点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定
逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,-300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
Q( 3,240°)
Q( 3,-120°)
Q( 3,600°)
Q( 3,-500°)
2.(2019江苏无锡外国语学校月考)如图23-2-1-11,点O是□ABCD的对称中心,AD>AB,点E、F在边AB上,且AB=2EF,点G、H在边BC上,且BC= 3GH,则△EOF和△GOH的面积比为_________.
九年级数学上册 23. 2.1中心对称
基础闯关全练
1.A 根据中心对称的定义知选A.
2.D ∵△ABC与△DEF成中心对称,∴对称中心是线段FC的中点,故选D.
3.答案 =;EF;DF
解析 ∵△ABC与△DEF关于点O成中心对称,
∴△ABC≌△DEF,
∴AB=DE,AC=DF.
易知△BOC≌△EOF,∴∠BCO= ∠EFO,∴BC∥EF.
4.解析(1)如图:
(2)点D的位置共有三种可能,如图:
能力提升全练
1.A 根据题意分析可得△DEC可以由△ABC经过:①以AC所在直线为对称轴作轴对称,再以C为旋转中心,顺时针旋转90°得到,故正确;②以C为旋转中心,顺时针旋转90°得
△A'B'C,再以A'C所在直线为对称轴作轴对称变化得到,故正确;③将△ABC向下、向左各平移1个单位,所得三角形与△DEC为轴对称图形,以AC的中点为中心,作中心对称得不
到△DEC,故错误.
2.答案 12
解析 当AP= OP时,DP+BQ的值最小,此时P为OA的中点,∴DP=OA.∵△AOD和△COB关于点O中心对称,∴OD= OB,且O,B,D三点共线,又BD=12,∴OD=6.∵∠ADO=90°,∠AOD=60°,∴AO=20D= 12,∴DP=6,同理BQ=6,∴DP+BQ的最小值为6+6= 12.
三年模拟全练
一、选择题
1.D 对应点的连线被对称中心O平分,A,B中结论正确;成中心对称的两个图形是全等图形,那么对应线段相等,C中结论正确,故选D.
二、填空题
2.答案 6;40
解析 ∵△CDA与△ABC关于点O中心对称,AB=6,∠BAC=40°,∴ CD=AB=6,∠ACD= ∠BAC=40°.
三、解答题
3.解析 (1)如图,△A₁B₁C₁即为所求.
(2)由图可知A₁(2,1),B₁(1,3).
五年中考全练
解答题
解析 (1)如图所示,△A₁B₁C₁即为所求.
(2)由题易知,点A'的坐标为(-2,2).
若要使点A'向右平移后落在△A₁B₁C₁的内部(不包括顶点和边界),则4
核心素养全练
1.D 由点P与点Q关于点O成中心对称可得,点Q的极坐标为(3,240°)或(3,-120°)或(3,600°).故选D.
2.答案 3:2
解析 连接AC、BD,∵点O是□ABCD的对称中心,∴AC、BD交于点O,∴,∵AB=2EF,∴,∵BC=3GH,∴,∴.
23.3 课题学习 图案设计
基础训练
1.已知:图A、图B分别是6×6正方形网格上的两个轴对称图形(阴影部分),其面积分别为、(网格中最小的正方形面积为一个平方单位),请观察图形并解答下列问题.
(1)填空: 的值是_________;
(2)请在图C的网格上画出一个面积为8个平方单位的中心对称图形.
2.如图中的图案是由一个怎样的基本图形经过旋转、轴对称和平移得到的呢?
[来源:学&科&网]
3.请你用基本图形 经过旋转、平移和轴对称设计一个美丽的图案。
能力提升
1.在右图的方框中做出以O为旋转中心旋转后的图形.
[来源:ZXXK]
2.利用你所学过的图形变换的知识设计一个图案,
参考答案[来源:学#科#网]
基础训练 1.(1)9∶11;(2)略.2.略。
能力提升1.图略.2.略
[来源:]
人教版九年级上册第二十三章 旋转综合与测试练习: 这是一份人教版九年级上册第二十三章 旋转综合与测试练习,共5页。
初中数学人教版九年级上册第二十三章 旋转综合与测试课时练习: 这是一份初中数学人教版九年级上册第二十三章 旋转综合与测试课时练习,共5页。试卷主要包含了选择题,填空题,解答题,附加题等内容,欢迎下载使用。
初中数学人教版九年级上册第二十三章 旋转综合与测试巩固练习: 这是一份初中数学人教版九年级上册第二十三章 旋转综合与测试巩固练习,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













