
北师大版九年级上册第六章 反比例函数综合与测试精品课时训练
展开这是一份北师大版九年级上册第六章 反比例函数综合与测试精品课时训练,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题(本大题共10小题,每小题3分,共30分)
1、如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y=B.y=C.y=D.y=
2、若A(2,4)与B(﹣2,a)都是反比例函数y=kx(k≠0)图象上的点,则a的值是( )
A.4B.﹣4C.2D.﹣2
3、已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y=kx(k<0)的图象上,且x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A.y2>y1>y3B.y3>y2>y1C.y1>y2>y3D.y3>y1>y2
4、如图,A、B是反比例函数y=2x的图象上关于原点O对称的任意两点,过点A作AC⊥x轴于点C,连接BC,则△ABC的面积为( )
A.1B.2C.3D.4
5、反比例函数y=kx在第一象限内的图象如图,点P是图象上一点,PQ⊥x轴,垂足为Q.若△POQ的面积为2,则k的值为( )
A.1B.2C.4D.2
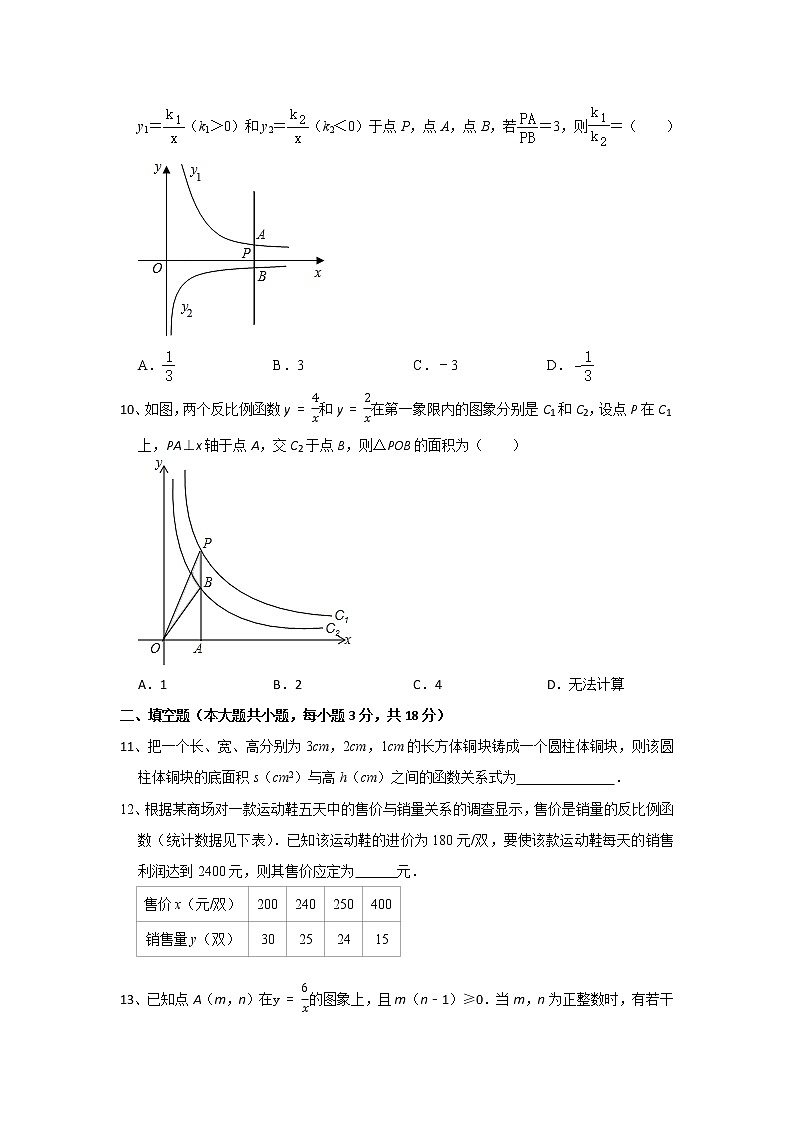
6、一款便携式音箱以锂电池作为电源,该电池的电压为定值,工作时电流I(单位:A)与电阻R(单位:Ω)之间的函数关系如图所示,则当电阻R为4Ω时,电流I为( )
A.6AB.32AC.1AD.23A
7、如图,一次函数y=-43x与反比例函数y=kx的图象交于A,B两点,点C在x轴上,连接AC,BC.若∠ACB=90°,△ABC的面积为20,则k的值是( )
A.﹣8B.﹣10C.﹣12D.﹣20
8、某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )
A.27分钟B.20分钟C.13分钟D.7分钟
9、如图,反比例函数y1=(k1>0)和y2=(k2<0)中,作直线x=10,分别交x轴,y1=(k1>0)和y2=(k2<0)于点P,点A,点B,若=3,则=( )
A.B.3C.﹣3D.
10、如图,两个反比例函数y=4x和y=2x在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )
A.1B.2C.4D.无法计算
二、填空题(本大题共小题,每小题3分,共18分)
11、把一个长、宽、高分别为3cm,2cm,1cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积s(cm2)与高h(cm)之间的函数关系式为 .
12、根据某商场对一款运动鞋五天中的售价与销量关系的调查显示,售价是销量的反比例函数(统计数据见下表).已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 元.
13、已知点A(m,n)在y=6x的图象上,且m(n﹣1)≥0.当m,n为正整数时,有若干满足题意的A点坐标,并从中随机抽取一个点,求在直线y=﹣x+6下方的概率 .
14、反比例函数y=-4x(x<0)如图所示,则矩形OAPB的面积是 .
15、某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160kPa时,气球将爆炸,为了安全,气球的体积V的范围是 .
16、如图,直线y=x+n与y轴的正半轴交于点A,与双曲线y=6x交于点P,Q(点Q在第一象限内),过点Q作QB⊥x轴于点B,若S△AOP﹣S梯形AOBQ=6,则n的值为 .
三、解答题(本大题共6小题,共72分.解答时应写出文字说明、证明过程或演算步骤)
17、已知矩形的面积是6cm2.它的一组邻边长分别是x(单位:cm)和y(单位:cm).
(1)写出y与x之间的函数关系式.并求出自变量的取值范围.
(2)画出这个函数的图象.
18、若函数y=(m﹣2)xm2-5是y关于x的反比例函数.
(1)求m的值;
(2)函数图象在哪些象限?在每个象限内,y随x的增大而怎样变化?
(3)当﹣3≤x≤-12时,求y的取值范围.
19、如图,点A、B分别在函数y1=2x(x>0)与y1=-2x(x<0)的图象上,A、B的横坐标分别为a、b.
(1)求△OAB的面积(用含a、b的式子表示);
(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值.
20、据报道,从2018年8月以来,“非洲猪瘟”给生猪养殖户带来了不可估量的损失.某养殖户为了预防“非洲猪瘟”的侵袭,每天对猪场进行药熏消毒,已知一瓶药物释放过程中,一个圈舍内每立方米空气中含药量y(毫克)与时间x(分钟)之间满足正比例函数关系;药物释放完后,y与x之间满足反比例函数关系,如图所示,结合图中提供的信息解答下列问题:
(1)分别求当0≤x≤10和x>10时,y与x之间满足的函数关系式;
(2)据测定,当空气中每立方米的含药量不低于6毫克时,消毒才有效,那么这次熏药的有效消毒时间是多少分钟.
21、如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,直线AB与反比例函数y=mx(m>0)在第一象限的图象交于点C、点D,其中点C的坐标为(1,8),点D的坐标为(4,n).
(1)分别求m、n的值;
(2)连接OD,求△ADO的面积.
22、如图,点A在反比例函数y=kx的图象在第二象限内的分支上,AB⊥x轴于点B,O是原点,且△AOB的面积为1.试解答下列问题:
(1)比例系数k= ;
(2)在给定直角坐标系中,画出这个函数图象的另一个分支;
(3)当x>1时,写出y的取值范围.
23、疫情期间,某药店出售一批进价为2元的口罩,在市场营销中发现此口罩的日销售单价x(元)与日销售量y(只)之间有如下关系:
(1)猜测并确定y与x之间的函数关系式;
(2)设经营此口罩的销售利润为W元,求出W与x之间的函数关系式,
(3)若物价局规定此口罩的售价最高不能超过10元/只,请你求出当日销售单价x定为多少时,才能获得最大日销售利润?最大利润是多少元?
24、如图,点A(32,4),B(3,m)是直线AB与反比例函数y=nx(x>0)图象的两个交点,AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
(1)求反比例函数和直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2,求S2﹣S1.
参考答案
一、选择题(本大题共10小题,每小题3分,共30分)
1、如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y=B.y=C.y=D.y=
【解答】解:∵等腰三角形的面积为10,底边长为x,底边上的高为y,
∴xy=10,
∴y与x的函数关系式为:y=.
故选:C.
2、若A(2,4)与B(﹣2,a)都是反比例函数y=kx(k≠0)图象上的点,则a的值是( )
A.4B.﹣4C.2D.﹣2
【解析】∵A(2,4)与B(﹣2,a)都是反比例函数y=kx(k≠0)图象上的点,
∴k=2×4=﹣2a,
∴a=﹣4,
故选:B.
3、已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y=kx(k<0)的图象上,且x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A.y2>y1>y3B.y3>y2>y1C.y1>y2>y3D.y3>y1>y2
【解析】∵反比例函数y=kx(k<0)的图象分布在第二、四象限,
在每一象限y随x的增大而增大,
而x1<x2<0<x3,
∴y3<0<y1<y2.
即y2>y1>y3.
故选:A.
4、如图,A、B是反比例函数y=2x的图象上关于原点O对称的任意两点,过点A作AC⊥x轴于点C,连接BC,则△ABC的面积为( )
A.1B.2C.3D.4
【解析】由题意可知:△AOC的面积为1,
∵A、B关于原点O对称,
∴△AOC与△BOC的面积相等,
∴S△ABC=2S△AOC=2,
故选:B.
5、反比例函数y=kx在第一象限内的图象如图,点P是图象上一点,PQ⊥x轴,垂足为Q.若△POQ的面积为2,则k的值为( )
A.1B.2C.4D.2
【解析】∵反比例函数的解析式为y=kx,
∵△POQ的面积为2,
∴12|k|=2,
∴|k|=4,
∴k=±4,
∵反比例函数y=kx在第一象限,
∴k=4;
故选:C.
6、一款便携式音箱以锂电池作为电源,该电池的电压为定值,工作时电流I(单位:A)与电阻R(单位:Ω)之间的函数关系如图所示,则当电阻R为4Ω时,电流I为( )
A.6AB.32AC.1AD.23A
【解析】设用电阻R表示电流I的函数解析式为I=kR,
∵反比例函数图象过(2,3),
∴k=3×2=6,
∴I=6R,
当R=4Ω时,I=64=32,
故选:B.
7、如图,一次函数y=-43x与反比例函数y=kx的图象交于A,B两点,点C在x轴上,连接AC,BC.若∠ACB=90°,△ABC的面积为20,则k的值是( )
A.﹣8B.﹣10C.﹣12D.﹣20
【解析】设点A为(a,-43a),
则OA=a2+(43a)2=-53a,
∵点C为x轴上一点,∠ACB=90°,且△ACB的面积为20,
∴OA=OB=OC=-53a,
∴S△ACB=12×OC×(yA+|yB|)=12×(-53a)×(-83a)=20,
解得,a=±3(舍弃3),
∴点A为(﹣3,4),
∴k=﹣3×4=﹣12,
故选:C.
8、某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )
A.27分钟B.20分钟C.13分钟D.7分钟
【解答】解:∵开机加热时每分钟上升10℃,
∴从30℃到100℃需要7分钟,
设一次函数关系式为:y=k1x+b,
将(0,30),(7,100)代入y=k1x+b得k1=10,b=30
∴y=10x+30(0≤x≤7),令y=50,解得x=2;
设反比例函数关系式为:y=,
将(7,100)代入y=得k=700,
∴y=,
将y=35代入y=,解得x=20;
∴水温从100℃降到35℃所用的时间是20﹣7=13分钟,
故选:C.
9、如图,反比例函数y1=(k1>0)和y2=(k2<0)中,作直线x=10,分别交x轴,y1=(k1>0)和y2=(k2<0)于点P,点A,点B,若=3,则=( )
A.B.3C.﹣3D.
【解答】解:∵点A在反比例函数y1=y1=(k1>0)的图象上,点B在反比例函数y2=(k2<0)的图象上,且=3,
∴k1=OP•PA,k2=﹣OP•BP,
∴==﹣3,
故选:C.
如图,两个反比例函数y=4x和y=2x在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )
A.1B.2C.4D.无法计算
【解析】∵PA⊥x轴于点A,交C2于点B,
∴S△POA=12×4=2,S△BOA=12×2=1,
∴S△POB=2﹣1=1.
故选:A.
二、填空题(本大题共小题,每小题3分,共18分)
11、把一个长、宽、高分别为3cm,2cm,1cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积s(cm2)与高h(cm)之间的函数关系式为 .
【解答】解:由题意可得:sh=3×2×1,
则s=.
故答案为:s=.
12、根据某商场对一款运动鞋五天中的售价与销量关系的调查显示,售价是销量的反比例函数(统计数据见下表).已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 元.
【解答】解:由表中数据得:xy=6000,
∴y=,
则所求函数关系式为y=;
由题意得:(x﹣180)y=2400,
把y=代入得:(x﹣180)•=2400,
解得:x=300,
经检验,x=300是原方程的根,
答:若计划每天的销售利润为2400元,则其单价应定为300元.
故答案为:300.
13、已知点A(m,n)在y=6x的图象上,且m(n﹣1)≥0.当m,n为正整数时,有若干满足题意的A点坐标,并从中随机抽取一个点,求在直线y=﹣x+6下方的概率 12 .
【解析】∵点A(m,n)在y=6x的图象上,
∴mn=6,
又∵m,n为正整数,
∴A点坐标可能为:(1,6),(2,3),(3,2),(6,1),共4种情况,
其中(2,3),(3,2)在直线y=﹣x+6下方,有2种情况,
∴从满足题意的A点坐标中随机抽取一个点,在直线y=﹣x+6下方的概率为24=12,
故答案为:12.
14、反比例函数y=-4x(x<0)如图所示,则矩形OAPB的面积是 4 .
【解析】设P点的坐标为(x,y),
∵P在反比例函数y=-4x(x<0)的图象上,
∴xy=﹣4,
即PB×PA=4,
∴矩形OAPB的面积是4,
故答案为:4.
15、某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160kPa时,气球将爆炸,为了安全,气球的体积V的范围是 V≥35 .
【解析】设球内气体的气压P(kPa)和气体体积V(m3)的关系式为P=kV,
∵图象过点(1.5,64),
∴k=96,
即P=96V,在第一象限内,P随V的增大而减小,
∴当P≤160时,V=96V≥35.
故答案为:V≥35.
16、如图,直线y=x+n与y轴的正半轴交于点A,与双曲线y=6x交于点P,Q(点Q在第一象限内),过点Q作QB⊥x轴于点B,若S△AOP﹣S梯形AOBQ=6,则n的值为 32 .
【解析】设:点P、Q的坐标分别为(x1,y1)、(x2、y2),则x2y2=6,
直线y=x+n与y轴的正半轴交于点A,则OA=n,
联立直线与反比例函数表达式并整理得:x2+nx﹣6=0,
则x1+x2=﹣n,
S△AOP﹣S梯形AOBQ=6,
即:12×OA×|x1|-12(AO+y2)x2=6,
即:AO(x1+x2)+x2y2=﹣12,
即﹣n2=﹣18,
解得:n=32(舍去负值),
故答案为:32.
三、解答题(本大题共6小题,共72分.解答时应写出文字说明、证明过程或演算步骤)
17、已知矩形的面积是6cm2.它的一组邻边长分别是x(单位:cm)和y(单位:cm).
(1)写出y与x之间的函数关系式.并求出自变量的取值范围.
(2)画出这个函数的图象.
【解答】解:(1)∵矩形的面积是6cm2.它的一组邻边长分别是x(单位:cm)和y(单位:cm),
∴xy=6,
故y与x之间的函数关系式为:y=,自变量的取值范围是:x>0;
(2)如图所示:
.
18、若函数y=(m﹣2)xm2-5是y关于x的反比例函数.
(1)求m的值;
(2)函数图象在哪些象限?在每个象限内,y随x的增大而怎样变化?
(3)当﹣3≤x≤-12时,求y的取值范围.
【分析】(1)根据反比例函数的定义列出关于m的不等式组,求出m的值即可;
(2)根据反比例函数的性质即可得出结论;
(3)分别令x=﹣3,x=-12,求出y的对应值即可.
【解析】(1)∵函数y=(m﹣2)xm2-5是y关于x的反比例函数,
∴m-2≠0m2-5=-1,解得m=﹣2;
(2)∵m=﹣2,
∴反比例函数的关系式为:y=-4x.
∵﹣4<0,
∴函数图象的两个分支分别位于第二四象限,且在每个象限内,y随x的增大而增大;
(3)∵反比例函数的关系式为:y=-4x,
∴当x=﹣3时,y=43;当x=-12时,y=8,
∴43≤y≤8.
19、如图,点A、B分别在函数y1=2x(x>0)与y1=-2x(x<0)的图象上,A、B的横坐标分别为a、b.
(1)求△OAB的面积(用含a、b的式子表示);
(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值.
【解析】作AC⊥x轴于C,BD⊥x轴于D,
∴AC∥BD∥y轴,
根据题意得A、B的纵坐标分别为2a,-2b,
∴CD=OC+OD=a﹣b,
∴S△AOB=S梯形ABDC-S△AOC-S△BOD=12⋅CD⋅(AC+BD)=12(a-b)(2a-2b)=-(a-b)2ab;
(2)根据两点间的距离公式得到OA2=a2+(2a)2,OB2=b2+(-2b)2,
∵△OAB是以AB为底边的等腰三角形,
∴OA=OB,
∴a2+(2a)2=b2+(-2b)2,
∴(a+b)(b-b)(1-4a2b2)=0,
∵a+b≠0,a>0,b<0,
∴1-4a2b2=0,
∴ab=2.
20、据报道,从2018年8月以来,“非洲猪瘟”给生猪养殖户带来了不可估量的损失.某养殖户为了预防“非洲猪瘟”的侵袭,每天对猪场进行药熏消毒,已知一瓶药物释放过程中,一个圈舍内每立方米空气中含药量y(毫克)与时间x(分钟)之间满足正比例函数关系;药物释放完后,y与x之间满足反比例函数关系,如图所示,结合图中提供的信息解答下列问题:
(1)分别求当0≤x≤10和x>10时,y与x之间满足的函数关系式;
(2)据测定,当空气中每立方米的含药量不低于6毫克时,消毒才有效,那么这次熏药的有效消毒时间是多少分钟.
【解析】(1)当0≤x≤10,设y与x之间满足的函数关系式为y=kx,
∵过点(10,30),
∴30=10k,
解得:k=3,
∴y=3x(0≤x≤10),
x>10时,设y与x之间满足的函数关系式为y=kx,
∵过点(10,30),
∴30=k10,
k=300,
∴y=300x(x>10);
(2)y=3x(0≤x≤10)中,当y≥6时,x≥2,
y=300x(x>10)中,当y≥6时,x≤50,
∴2≤x≤50,
∴这次熏药的有效消毒时间是:50﹣2=48(分钟)
答:这次熏药的有效消毒时间是48分钟.
21、如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,直线AB与反比例函数y=mx(m>0)在第一象限的图象交于点C、点D,其中点C的坐标为(1,8),点D的坐标为(4,n).
(1)分别求m、n的值;
(2)连接OD,求△ADO的面积.
【解析】(1)∵反比例函数y=mx(m>0)在第一象限的图象交于点C(1,8),
∴8=m1,
∴m=8,
∴函数解析式为y=8x,
将D(4,n)代入y=8x得,n=84=2.
(2)设直线AB的解析式为y=kx+b,由题意得 k+b=84k+b=2,
解得 k=-2b=10,
∴直线AB的函数解析式为y=﹣2x+10,
令x=0,则y=10,
∴A(0,10),
∴△ADO的面积=12×10×4=20=20.
22、如图,点A在反比例函数y=kx的图象在第二象限内的分支上,AB⊥x轴于点B,O是原点,且△AOB的面积为1.试解答下列问题:
(1)比例系数k= ﹣2 ;
(2)在给定直角坐标系中,画出这个函数图象的另一个分支;
(3)当x>1时,写出y的取值范围.
【解答】(1)解:由于△AOB的面积为1,则|k|=2,又函数图象位于第一象限,k>0,
则k=2,反比例函数关系式为y=-2x.
故答案为:﹣2;
(2)如图所示:
;
(3)利用图象可得出:
当x>1时:﹣2<y<0.
23、疫情期间,某药店出售一批进价为2元的口罩,在市场营销中发现此口罩的日销售单价x(元)与日销售量y(只)之间有如下关系:
(1)猜测并确定y与x之间的函数关系式;
(2)设经营此口罩的销售利润为W元,求出W与x之间的函数关系式,
(3)若物价局规定此口罩的售价最高不能超过10元/只,请你求出当日销售单价x定为多少时,才能获得最大日销售利润?最大利润是多少元?
【解析】(1)由表可知,xy=6000,
∴y=6000x (x>0);
(2)根据题意,得:
W=(x﹣2)•y=(x﹣2)•6000x=6000-12000x;
(3)∵x≤10,
∴6000-12000x≤4800,
即当x=10时,W取得最大值,最大值为4800元,
答:当日销售单价x定为10元/个时,才能获得最大日销售利润,最大利润是4800元.
24、如图,点A(32,4),B(3,m)是直线AB与反比例函数y=nx(x>0)图象的两个交点,AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
(1)求反比例函数和直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2,求S2﹣S1.
【解析】(1)由点A(32,4)在反比例函数y=nx(x>0)图象上,
∴4=n3,解得n=6,
∴反比例函数的解析式为y=6x(x>0),
将点B(3,m)代入y=6x(x>0)并解得m=2,
∴B(3,2),
设直线AB的表达式为y=kx+b,
∴4=32k+b2=3k+b,解得k=-43b=6,
∴直线AB的表达式为y=-43x+6;
(2)由点A坐标得AC=4,
则点B到AC的距离为3-32=32,
∴S1=12×4×32=3,
设AB与y轴的交点为E,则点E(0,6),如图:
∴DE=6﹣1=5,
由点A(32,4),B(3,2)知,点A,B到DE的距离分别为32,3,
∴S2=S△BDE-S△AED=12×5×3-12×5×32=154,
∴S2-S1=154-3=34.
售价x(元/双)
200
240
250
400
销售量y(双)
30
25
24
15
日销售单价x(元)
3
4
5
6
日销售量y(只)
2000
1500
1200
1000
售价x(元/双)
200
240
250
400
销售量y(双)
30
25
24
15
日销售单价x(元)
3
4
5
6
日销售量y(只)
2000
1500
1200
1000
相关试卷
这是一份数学九年级上册1 反比例函数单元测试测试题,共6页。试卷主要包含了选择题,四象限,则k的取值可以是,解答题等内容,欢迎下载使用。
这是一份初中数学北师大版九年级上册第六章 反比例函数1 反比例函数精品精练,文件包含单元复习卷北师大版数学九年级上册--第六章反比例函数单元复习试卷教师版doc、单元复习卷北师大版数学九年级上册--第六章反比例函数单元复习试卷学生版doc等2份试卷配套教学资源,其中试卷共14页, 欢迎下载使用。
这是一份北师大版九年级上册第六章 反比例函数综合与测试随堂练习题,共21页。试卷主要包含了单选题,解答题等内容,欢迎下载使用。













