初中北师大版第四章 三角形3 探索三角形全等的条件多媒体教学ppt课件

这是一份初中北师大版第四章 三角形3 探索三角形全等的条件多媒体教学ppt课件，共26页。PPT课件主要包含了温故知新，想一想，两边及夹角，两边及其一边的对角，归纳总结，学以致用，变式训练，拓展提升，达标检测，①③④等内容，欢迎下载使用。

教学内容分析本节课选自北师大版《七年级数学下册》第四章第三节探索三角形全等的条件第三课时。在前两课时已探索了三角形的三种判定：SSS，ASA，AAS，本节课探索第四种判定方法—-----边角边（SAS），为了使学生更好地掌握这一部分内容，遵循启发式教学原则，利用类比的思想，通过回顾类比，引导学生操作、观察、探索、发现、归纳，真正把学生放到主体位置，体会分析问题、解决问题的方法，积累数学活动经验，为以后的证明打下基础。
学生学习情况分析学生的知识技能基础：学生在前两节课的学习中，已经探索了三角形全等的条件——SSS，ASA，AAS，利用实验验证了其正确性，并会进行简单的证明，对本节课要学习的三角形全等条件中的“边角边”来说已经具备了一定的知识技能基础。学生活动经验基础：在前两节课及前面学习过程中，学生已经经历了一些探索图形全等的活动，通过作图，折纸，比较等方式验证三角形的全等，获得了一些数学活动经验的基础。
设计思想在这之前学生已掌握尺规作图的方法，并在之前两节课探索了三角形全等的条件（SSS、ASA、AAS），这为探究三角形全等的条件3（SAS）做好了知识上的准备。另外，学生也基本具备了利用尺规做三角形的能力，具备探索的热情和愿望，这使学生能主动参与本节课的操作、探究。遵循启发式教学原则，采用问题形式引入课题激起学生探索问题的热情。通过回顾类比，引导学生操作、观察、探索、发现、归纳，真正把学生放到主体位置，体会分析问题、解决问题的方法。
　1．探索并正确理解三角形全等的判定方法“SAS”;（重点）　2．会用“SAS”判定方法证明两个三角形全等及进行简单的应用;（重点） 3.了解“SSA”不能作为两个三角形全等的条件.（难点）　
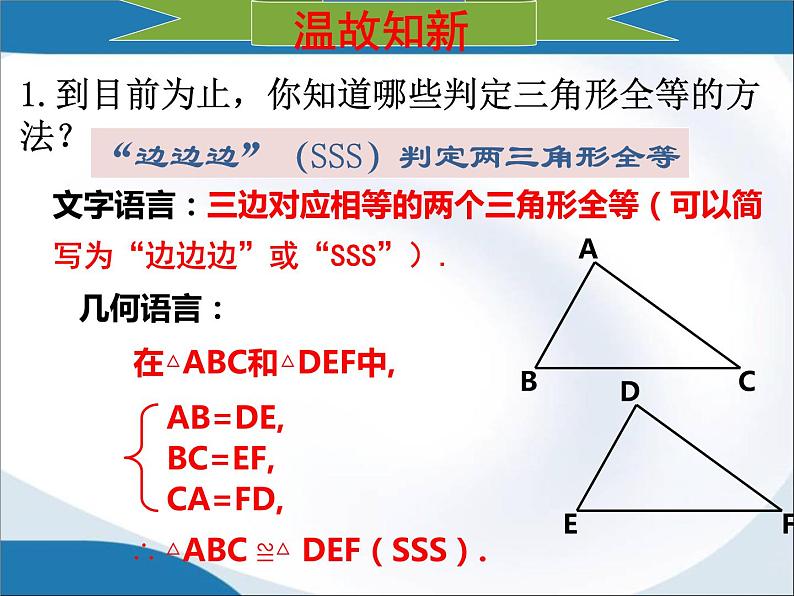
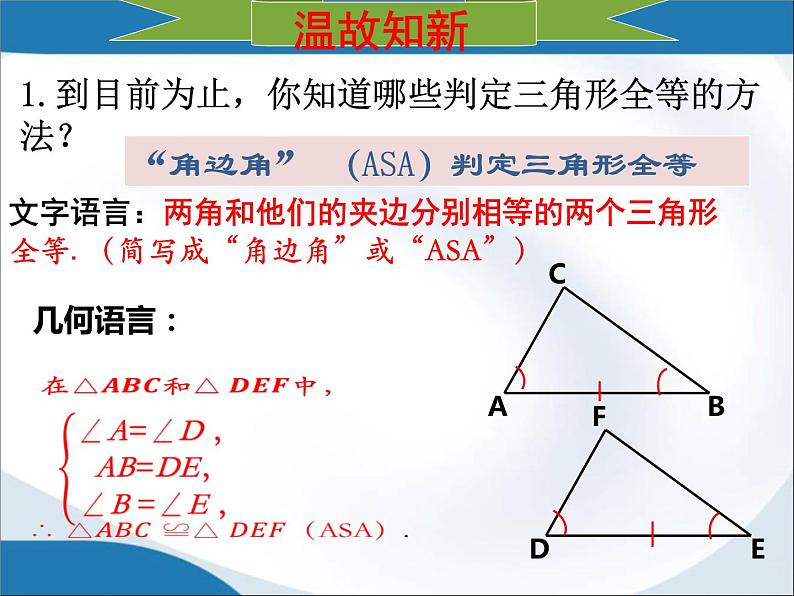
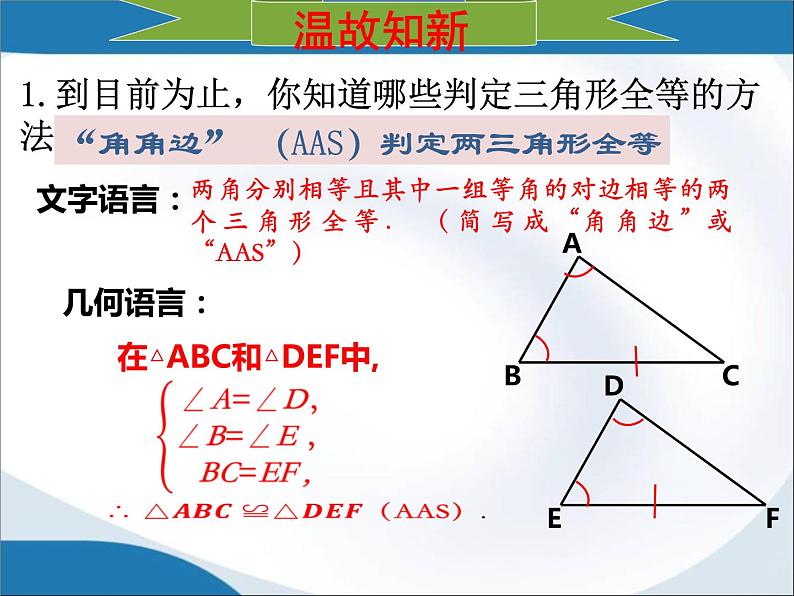
1.到目前为止，你知道哪些判定三角形全等的方法？
文字语言：三边对应相等的两个三角形全等（可以简写为“边边边”或“SSS”）.
“边边边”（SSS）判定两三角形全等
文字语言：两角和他们的夹边分别相等的两个三角形全等.（简写成“角边角”或“ASA”）
“角边角” （ASA）判定三角形全等
如图线段AB是一个池塘的长度，现在想测量这个池塘的长度，在水上测量不方便，你有什么好的方法较方便地把池塘的长度测量出来吗？想想看。通过回顾类比，不但引入了本课的课题，而且激发了学生的好奇心和求知欲，调动了学生的学习积极性，使他们体会探索的过程是为了解决问题的实际需要。通过问题情境的创设，不但引入了本课的课题，而且激发了学生的好奇心和求知欲，调动了学生的学习积极性，使他们体会探索的过程是为了解决问题的实际需要。联系生活，充分调动学生的积极性
小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结CD，用米尺测出DE的长，这个长度就等于A，B两点的距离。你知道小明的依据吗？
通过问题情境的创设，不但引入了本课的课题，而且激发了学生的好奇心和求知欲，调动了学生的学习积极性，使他们体会探索的过程是为了解决问题的实际需要。联系生活，充分调动学生的积极性
只知道三角形的两边及一角，有几种可能的情况呢？
三角形两边分别为2.5cm，3.5cm，它们所夹的角为40°，你能画出这个三角形吗？你画的三角形与同伴画的一定全等吗？
△ABC就是所求三角形
结论：在两个三角形中，如果有两条边及它们的夹角对应相等，那么这两个三角形全等.
从实践操作中，引发总结，将前面画图的结果升华成理论，让学生学会思考，善于思考。参与构建对知识的形成和体验。
两条边的长分别为2.5cm，3.5cm，长度为2.5cm的边所对的角为40°，情况又怎样？动手画一画，你发现了什么？
作法：（1）画一线段AC，使它等于3.5cm,（2）画∠CAM= ；（3）以C为圆心，2.5cm长为半径画弧交AM于点B；（4）连接BC.
△AB1C与△AB2C都符合所要求的三角形
结论：两边及其中一边的对角相等，两个三角形无法确定全等.
培养学生调动学生的主观能动性，使学生积极主动地参与教学活动，使学生对两边及其一边的对角的条件得不到三角形全等有更直观的认识。并从不同三角形的画法说明两边及其一边的对角的条件得不到三角形全等的原因，使学生对SSA不能用于证明三角形的全等有更深刻的印象。
三角形全等的条件： 两边和它们的夹角对应相等的两个三角形全等，简写为“边角边”或“SAS”.
在△ ABC和△ DEF中．
所以△ABC ≌ △DEF．(SAS)
1.在下列图中找出全等三角形进行连线.
如图线段AB是一个池塘的长度，现在想测量这个池塘的长度，在水上测量不方便，你有什么好的方法较方便地把池塘的长度测量出来吗？想想看。
例 1 在△ABC中，AB=AC，AD是∠BAC的角平分线，(1)试说明:△ABD≌△ACD
(2)试说明： BD=DC
（2）∵ △ABD≌△ACD（已证） ∴BD=DC（全等三角形的性质）
解：∵AD是∠BAC的角平分线（已知）∴∠BAD＝∠CAD(角平分线的定义）
例2 如图，已知AB＝AC，DC＝BE,(1)求证：∠B＝∠C.
在△ABD和△ACE中 AB＝AC（已知）∠A＝∠A（公共角）　AD＝AE（已知）∴△ABD≌△ACD（SAS）∴∠B=∠C（全等三角形的性质）
(2)求证：EO＝DO
(2) 证明：在△BOE和△COD中， ∠B=∠C （已证）∠EOB＝∠COD（对顶角角）　BE＝DC（已知）∴△BOE≌△COD（AAS）∴ EO=DO（全等三角形的性质）
(1)证明：∵AB=AC，CD=BE（已知）∴AB-BE=AC-DC（等式的性质）即AE=AD
(3)若CE=5,OD＝1,求BO长
（3） ∵ △ABD≌△ACD（已证）∴BD=CE（全等三角形的性质）
∵ CE=5（已知）∴BD=5，∴BO=BD-OD=5-1=4（等式性质）
变式1：如图，∠B＝∠E，AB＝EF，BD＝EC，那么△ABC与　△FED全等吗？为什么？
AC∥FD吗？为什么？
解： △ABC与△FED全等.理由如下∵BD=EC（已知）　　　∴BD－CD＝EC－CD即BC=DED。即BC＝ED　　
（2）AC∥FD.理由如下∵ △ABC≌△FED（已证） ∴∠1＝∠2（全等三角形的性质）
∴∠3＝∠4（等角的补角相等）
∴AC∥FD（内错角相等，两直线平行）
变:2：如图，点E、F在AC上，AD//BC，AD=CB，AE=CF. 问：线段BE、DF有什么数量关系和位置关系？并加以说明.
∴ BE=DF,∴ ∠BEC=∠DFE（全等三角形的性质），
∴DF //BE（内错角相等两直线平行）
故线段BE、DF的数量关系为DF=BE，位置关系DF //BE.
变式3：已知:如图, AC=AB,AE=AD,∠BAC＝ ∠ DAE，（1）试说明:∠B=∠ACE.
在△ABD和△ACE中, AB＝AC(已知)， ∠DAB＝∠CAE(已证)， AD＝AE(已知)， ∴△ABD≌△ACE(SAS). ∴ ∠B=∠ACE(全等三角形的性质).
解:∵ ∠BAC＝ ∠ DAE(已知)， ∴∠BAC-∠DAC＝ ∠DAE- ∠DAC(等式的性质)， 即∠DAB＝∠CAE.
（2）若∠BAC=100°，求∠BCE.
（2）在△ABC中， ∠ BAC=100° ∠BAC+ ∠B+ ∠ BCA=180°（三角形内角和定理）∴ ∠B+ ∠ BCA=80°
在△ABC中， ∠ BAC=100° ∵ ∠B=∠ACE（已证）∴ ∠ACE+ ∠ BCA=80°即∠BCE= 80°
如图已知AB=AE，∠B=∠E，BC=ED，F是CD的中点，试说明AF⊥CD
∴△ABC≌△ADE（SSS）∴ ∠AFC=∠AFD（全等三角形的性质）
∴AF⊥CD（垂直定义）
1. 新的三角形全等的条件：两边和它们的夹角对应相等的两个三角形全等. (边角边或SAS)
2三角形全等判定方法：SSS，ASA，AAS，SAS
3. 注意对应边和对应角的确定，特别是公共边、公共角、角的平分线和中点的应用.
5.遇到较为复杂的图形时，可以采用图形分离法（将基本图形分离）.
6.无法直接证明三角形全等时，考虑辅助线的添加.
4.当已知条件给出的边相等（或角相等）不是所证的两个三角形的边（或角）时，可以利用相等线段（或角）的和或差求出所在的 三角形的边（或角）.
4.如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE.下列说法：①△ABD和△ACD的面积相等；②∠BAD＝∠CAD；③△BDF≌△CDE；④BF∥CE；⑤CE＝AE.其中正确的有 .(填序号)
5. 小明做了一个如图所示的风筝，其中∠EDH=∠FDH, ED=FD ，将上述条件标注在图中，小明不用测量就能知道EH=FH吗？与同桌进行交流。
必做题：课本P104 习题4.8 第1、2、4题．