人教版华师大北师大版等通用版 中考数学 专题08 函数之反比例函数问题（含解析）

专题08 函数之反比例函数问题

中考压轴题中函数之反比例函数问题，选择、填空和解答三种题型都有，内容主要包括反比例函数关系式的建立，反比例函数图象的分析，反比例函数的性质，反比例函数的应用四方面的内容。

一. 反比例函数关系式的建立：

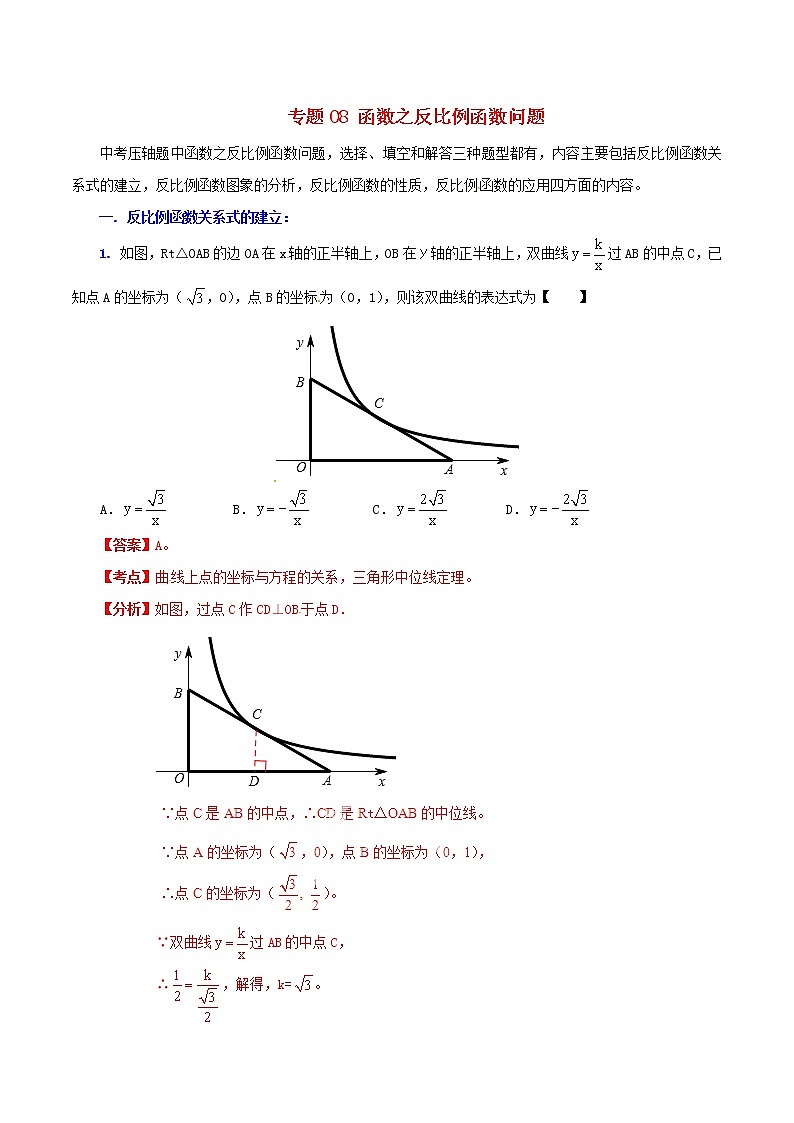
1. 如图，Rt△OAB的边OA在x轴的正半轴上，OB在ｙ轴的正半轴上，双曲线过AB的中点C，已知点A的坐标为（，0），点B的坐标为（0，1），则该双曲线的表达式为【    】

 A．        B．        C．       D．

【答案】A。

【考点】曲线上点的坐标与方程的关系，三角形中位线定理。

【分析】如图，过点C作CD⊥OB于点D．

∵双曲线过AB的中点C，

∴，解得，k=。

∴该双曲线的表达式为。

故选A。　

2. 如图，已知点A在反比例函数图象上，点B在反比例函数 (k≠0)的图象上，CB∥x轴，BD∥AO，若CA=CB，则双曲线的表达式为       。

【答案】。

【考点】反比例函数的图象和性质。

二. 反比例函数图象的分析：

3. 点A(x1，y1)、B(x2，y2)、C(x3，y3)都在反比例函数的图象上，且x1＜0＜x2＜x3，则y1、y2、y3的大小关系是【    】

A．y3＜y1＜y2          B．y1＜y2＜y3          C．y3＜y2＜y1          D．y2＜y3＜y1

【答案】D。

【考点】反比例函数的图象和性质，数形结合思想的应用。

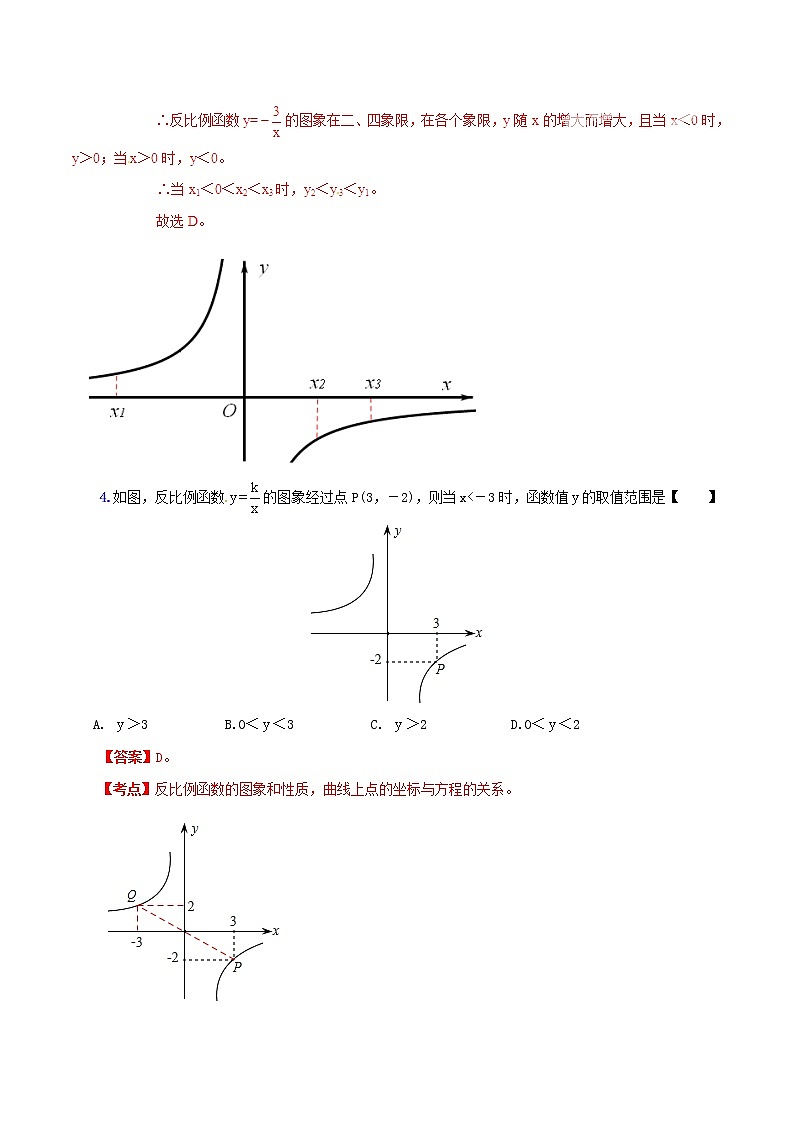
4.如图，反比例函数的图象经过点P(3，－2)，则当x<－3时，函数值的取值范围是【    】

A. ＞3           B.0＜＜3           C. ＞2            D.0＜＜2      

【答案】D。

【考点】反比例函数的图象和性质，曲线上点的坐标与方程的关系。

三. 反比例函数的性质：

5. 如图所示，点A是双曲线y=（x＞0）上的一动点，过A作AC⊥y轴，垂足为点C，作AC的垂直平分线双曲线于点B，交x轴于点D．当点A在双曲线上从左到右运动时，四边形ABCD的面积（　　）

A．逐渐变小             B．由大变小再由小变大

C．由小变大再有大变小   D．不变

【答案】D

【解析】

即四边形ABCD的面积不随C点的变化而变化．

故选D．

考点：反比例函数系数k的几何意义．

点评：本题主要考查的是利用反比例函数系数k的几何意义求对角线互相垂直的四边形面积的计算方法．

四. 反比例函数的应用：

6. 为了预防“非典”,某学校对教室采用药熏清毒法进行消毒, 已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x 的函数关系式为: ________, 自变量x 的取值范围是:_______,药物燃烧后y关于x的函数关系式为_______.

(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室;

(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?

【答案】(1)y=,0<x≤8,y=；(2)30；(3)此次消毒有效

【解析】

设药物燃烧后y关于x的函数关系式为（k2＞0）

代入（8，6）为，

∴k2=48

∴药物燃烧时y关于x的函数关系式为(1)y=，0<x≤8，药物燃烧后y关于x的函数关系式为y=（x＞8）；

（2）结合实际，令y=中y≤1.6得x≥30

即从消毒开始，至少需要30分钟后学生才能进入教室；