
还剩16页未读,
继续阅读
2020-2021学年安徽省淮南市田家庵区八年级(上)期中数学试卷 解析版
展开
2020-2021学年安徽省淮南市田家庵区八年级(上)期中数学试卷
一、选择题:(本大题10小题,每小题3分,共30分)
1.下列四个地铁标志中,是轴对称图形的是( )
A. B. C. D.
2.以下各组线段为边,能组成三角形的是( )
A.1cm,2cm,3cm B.1cm,3cm,5cm
C.2cm,3cm,4cm D.2cm,4cm,6cm
3.在平面直角坐标系中,点A关于x轴的对称点为A1(3,﹣2),则点A的坐标为( )
A.(3,2) B.(﹣3,﹣2) C.(3,﹣2) D.(﹣3、7)
4.一个多边形的每一个外角都等于36°,则这个多边形的边数n等于( )
A.8 B.10 C.12 D.14
5.三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的( )
A.三条中线的交点 B.三边垂直平分线的交点
C.三条高的交点 D.三条角平分线的交点
6.如图,已知△ABC的3条边和3个角,则能判断和△ABC全等的是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
7.如图,AD是△ABC的外角∠EAC的平分线,AD∥BC,∠B=32°,则∠C的度数是( )
A.64° B.32° C.30° D.40°
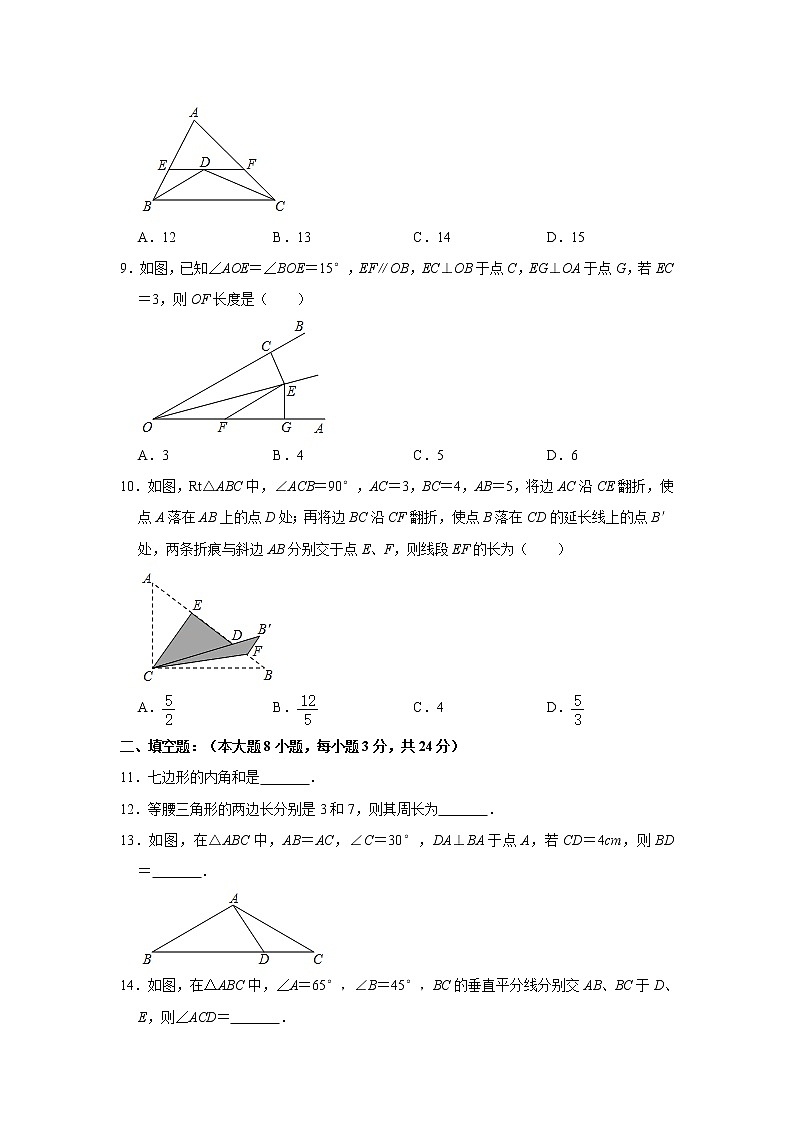
8.如图,△ABC中,AB=6,AC=9,BD、CD分别平分∠ABC,∠ACB过点D作直线平行于BC,分别交AB、AC于E、F,则△AEF的周长为( )
A.12 B.13 C.14 D.15
9.如图,已知∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C,EG⊥OA于点G,若EC=3,则OF长度是( )
A.3 B.4 C.5 D.6
10.如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段EF的长为( )
A. B. C.4 D.
二、填空题:(本大题8小题,每小题3分,共24分)
11.七边形的内角和是 .
12.等腰三角形的两边长分别是3和7,则其周长为 .
13.如图,在△ABC中,AB=AC,∠C=30°,DA⊥BA于点A,若CD=4cm,则BD= .
14.如图,在△ABC中,∠A=65°,∠B=45°,BC的垂直平分线分别交AB、BC于D、E,则∠ACD= .
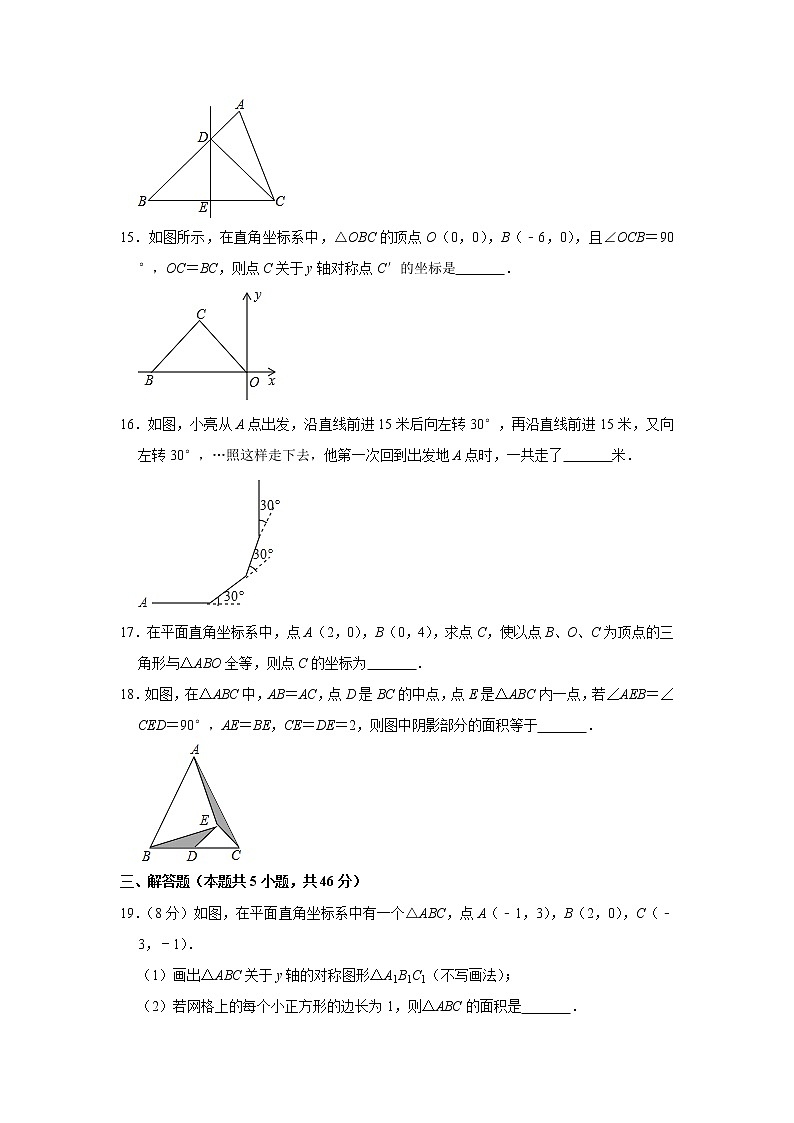
15.如图所示,在直角坐标系中,△OBC的顶点O(0,0),B(﹣6,0),且∠OCB=90°,OC=BC,则点C关于y轴对称点C′的坐标是 .
16.如图,小亮从A点出发,沿直线前进15米后向左转30°,再沿直线前进15米,又向左转30°,…照这样走下去,他第一次回到出发地A点时,一共走了 米.
17.在平面直角坐标系中,点A(2,0),B(0,4),求点C,使以点B、O、C为顶点的三角形与△ABO全等,则点C的坐标为 .
18.如图,在△ABC中,AB=AC,点D是BC的中点,点E是△ABC内一点,若∠AEB=∠CED=90°,AE=BE,CE=DE=2,则图中阴影部分的面积等于 .
三、解答题(本题共5小题,共46分)
19.(8分)如图,在平面直角坐标系中有一个△ABC,点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .
20.(8分)如图:已知点A、E、F、B在一条直线上,AE=BF,CF=DE,AC=BD,求证:GE=GF.
21.(8分)如图,已知:△ABC中,AB边上的垂直平分线DE交AB于D,交AC于E,△BCE的周长为16cm,△ABC的周长为24cm,求AD的长度.
22.(10分)如图,在△ABC中,AB=AC,点D在AB边上且点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)连接CD,若CD=CB,求∠B的度数.
23.(12分)如图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
(1)求∠AEB的度数.
(2)试证明AE=BE+2CM.
2020-2021学年安徽省淮南市田家庵区八年级(上)期中数学试卷
参考答案与试题解析
一、选择题:(本大题10小题,每小题3分,共30分)
1.下列四个地铁标志中,是轴对称图形的是( )
A. B. C. D.
【分析】直接利用轴对称图形的定义得出答案.
【解答】解:A、不是轴对称图形,不合题意;
B、是轴对称图形,符合题意;
C、不是轴对称图形,不合题意;
D、不是轴对称图形,不合题意.
故选:B.
2.以下各组线段为边,能组成三角形的是( )
A.1cm,2cm,3cm B.1cm,3cm,5cm
C.2cm,3cm,4cm D.2cm,4cm,6cm
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【解答】解:根据三角形的三边关系,知
A、1+2=3,不能组成三角形;
B、1+3<5,不能组成三角形;
C、2+3>4,能够组成三角形;
D、2+4=6,不能组成三角形.
故选:C.
3.在平面直角坐标系中,点A关于x轴的对称点为A1(3,﹣2),则点A的坐标为( )
A.(3,2) B.(﹣3,﹣2) C.(3,﹣2) D.(﹣3、7)
【分析】利用关于x轴的对称点的坐标特点进行解答即可.
【解答】解:∵点A关于x轴的对称点为A1(3,﹣2),
∴点A的坐标为(3,2),
故选:A.
4.一个多边形的每一个外角都等于36°,则这个多边形的边数n等于( )
A.8 B.10 C.12 D.14
【分析】多边形的外角和是固定的360°,依此可以求出多边形的边数.
【解答】解:∵一个多边形的每一个外角都等于36°,
∴多边形的边数为360°÷36°=10.
故选:B.
5.三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的( )
A.三条中线的交点 B.三边垂直平分线的交点
C.三条高的交点 D.三条角平分线的交点
【分析】根据线段垂直平分线的性质:线段垂直平分线上任意一点,到线段两端点的距离相等可得答案.
【解答】解:三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的三边垂直平分线的交点,
故选:B.
6.如图,已知△ABC的3条边和3个角,则能判断和△ABC全等的是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
【分析】首先观察图形,然后根据三角形全等的判定方法(AAS与SAS),即可求得答案.
【解答】解:如图:
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SAS);
在△ABC和△MNK中,
,
∴△ABC≌△MNK(AAS).
∴甲、乙、丙三个三角形中和△ABC全等的图形是:乙或丙.
故选:B.
7.如图,AD是△ABC的外角∠EAC的平分线,AD∥BC,∠B=32°,则∠C的度数是( )
A.64° B.32° C.30° D.40°
【分析】根据平行线的性质求出∠EAD,根据角平分线的定义得到∠EAC=2∠EAD=64°,根据三角形的外角性质计算即可.
【解答】解:∵AD∥BC,
∴∠EAD=∠B=32°,
∵AD是△ABC的外角∠EAC的平分线,
∴∠EAC=2∠EAD=64°,
∵∠EAC是△ABC的外角,
∴∠C=∠EAC﹣∠B=64°﹣32°=32°,
故选:B.
8.如图,△ABC中,AB=6,AC=9,BD、CD分别平分∠ABC,∠ACB过点D作直线平行于BC,分别交AB、AC于E、F,则△AEF的周长为( )
A.12 B.13 C.14 D.15
【分析】根据平行线的性质得到∠EDB=∠DBC,∠FDC=∠DCB,根据角平分线的性质得到∠EBD=∠DBC,∠FCD=∠DCB,等量代换得到∠EDB=∠EBD,∠FDC=∠FCD,于是得到ED=EB,FD=FC,即可得到结果.
【解答】解:∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB,
∵△ABC中,∠ABC和∠ACB的平分线相交于点D,
∴∠EBD=∠DBC,∠FCD=∠DCB,
∴∠EDB=∠EBD,∠FDC=∠FCD,
∴ED=EB,FD=FC,
∵AB=6,AC=9,
∴△AEF的周长为:AE+EF+AF=AE+ED+FD+AF=AE+EB+FC+AF=AB+AC=6+9=15.
故选:D.
9.如图,已知∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C,EG⊥OA于点G,若EC=3,则OF长度是( )
A.3 B.4 C.5 D.6
【分析】根据角平分线的性质得到EG的长度,再根据平行线的性质得到∠OEF=∠COE=15°,然后利用三角形的外角和内角的关系求出∠EFG=30°,利用30°角所对的直角边是斜边的一半,即可得到EF的长,进而得出OF的长.
【解答】解:∵∠AOE=∠BOE=15°,EC⊥OB于点C,EG⊥OA于点G,
∴CE=EG=3,
∵EF∥OB,
∴∠COE=∠OEF=15°
∴∠EFG=15°+15°=30°,∠EOF=∠OEF,
∴OF=EF=2EG=2×3=6.
故选:D.
10.如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段EF的长为( )
A. B. C.4 D.
【分析】根据翻折的性质可知角ECF为45度,根据等腰直角三角形的性质和三角形的面积即可求解.
【解答】解:根据两次翻折可知:
∠ACE=∠DCE,∠BCF=∠DCF,CE⊥AD,
∵∠ACB=90°,
∴∠ECF=∠ECD+∠FCD=∠ACB=45°,
∴∠EFC=45°,
∴EF=CE,
∵S△ABC=AC•BC=AB•CE,
∴5CE=3×4,CE=.
∴EF=.
故选:B.
二、填空题:(本大题8小题,每小题3分,共24分)
11.七边形的内角和是 900° .
【分析】由n边形的内角和是:180°(n﹣2),将n=7代入即可求得答案.
【解答】解:七边形的内角和是:180°×(7﹣2)=900°.
故答案为:900°.
12.等腰三角形的两边长分别是3和7,则其周长为 17 .
【分析】因为边为3和7,没明确是底边还是腰,所以有两种情况,需要分类讨论.
【解答】解:分两种情况:
当3为底时,其它两边都为7,3、7、7可以构成三角形,周长为17;
当3为腰时,其它两边为3和7,3+3=6<7,所以不能构成三角形,故舍去,
所以等腰三角形的周长为17.
故答案为:17.
13.如图,在△ABC中,AB=AC,∠C=30°,DA⊥BA于点A,若CD=4cm,则BD= 8cm .
【分析】根据等腰三角形的性质求出∠B=∠C=30°,根据三角形内角和定理求出∠BAC,求出∠DAC=∠C=30°,求出AD=CD=4cm,根据含30°角的直角三角形的性质求出即可.
【解答】解:∵在△ABC中,AB=AC,∠C=30°,
∴∠B=∠C=30°,
∴∠BAC=180°﹣∠C﹣∠B=120°,
∵DA⊥AB,
∴∠BAD=90°,
∴∠DAC=120°﹣90°=30°,
∴∠C=∠DAC=30°,
∵CD=4cm,
∴AD=CD=4cm,
在Rt△BAD中,∠BAD=90°,AD=4cm,∠B=30°,
∴BD=2AD=8cm,
故答案为:8cm.
14.如图,在△ABC中,∠A=65°,∠B=45°,BC的垂直平分线分别交AB、BC于D、E,则∠ACD= 25° .
【分析】在△ABC中,∠A=65°,∠B=45°,根据三角形内角和定理可得∠ACB=70°,再由线段垂直平分线的性质可得DB=DC,根据等边对等角得出∠DCB=∠B=45°,然后根据∠ACD=∠ACB﹣∠DCB,计算即可求解.
【解答】解:在△ABC中,∵∠A=65°,∠B=45°,
∴∠ACB=180°﹣∠A﹣∠B=70°,
∵DE是BC的垂直平分线,
∴DB=DC,
∴∠DCB=∠B=45°,
∴∠ACD=∠ACB﹣∠DCB=70°﹣45°=25°.
故答案为25°.
15.如图所示,在直角坐标系中,△OBC的顶点O(0,0),B(﹣6,0),且∠OCB=90°,OC=BC,则点C关于y轴对称点C′的坐标是 (3,3) .
【分析】过点C作CD⊥OB于D,根据等腰直角三角形的性质可得CD=OD=OB,从而求出点C的坐标,再根据关于y轴对称的点,纵坐标相同,横坐标互为相反数求解即可.
【解答】解:如图,过点C作CD⊥OB于D,
∵∠OCB=90°,OC=BC,
∴△BOC是等腰直角三角形,
∴CD=OD=OB,
∵O(0,0),B(﹣6,0),
∴OB=6,
∴CD=OD=×6=3,
∴点C的坐标为(﹣3,3),
∴点C关于y轴对称点C′的坐标是(3,3).
故答案为:(3,3).
16.如图,小亮从A点出发,沿直线前进15米后向左转30°,再沿直线前进15米,又向左转30°,…照这样走下去,他第一次回到出发地A点时,一共走了 180 米.
【分析】由题意可知小亮所走的路线为一个正多边形,根据多边形的外角和即可求出答案.
【解答】解:∵360÷30=12,
∴他需要走12次才会回到原来的起点,即一共走了15×12=180(米).
故答案为:180.
17.在平面直角坐标系中,点A(2,0),B(0,4),求点C,使以点B、O、C为顶点的三角形与△ABO全等,则点C的坐标为 (﹣2,0)或(2,4)或(﹣2,4) .
【分析】由条件可知BO为两三角形的公共边,且△ABO为直角三角形,当△ABO和△BCO全等时,则可知△BCO为直角三角形,且有CO=AO可BC=AO,可得出C点的坐标.
【解答】解:∵点A(2,0),B(0,4),
∴AO=2,且△ABO为直角三角形,
当△ABO和△BCO全等时,则可知△BCO为直角三角形,且有公共边BO,
∴CO=AO或BC=AO,
当CO=AO时,则C点坐标为(﹣2,0);
当BC=AO时,则BC=2,且BC⊥OB,
∴C点坐标为(2,4)或(﹣2,4);
综上可知点C的坐为(﹣2,0)或(2,4)或(﹣2,4),
故答案为:(﹣2,0)或(2,4)或(﹣2,4).
18.如图,在△ABC中,AB=AC,点D是BC的中点,点E是△ABC内一点,若∠AEB=∠CED=90°,AE=BE,CE=DE=2,则图中阴影部分的面积等于 4 .
【分析】作GD⊥BE于G,作CF⊥AE于F,可证△DEG≌△CEF可得DG=CF,则S△BDE=S△AEC,由D是BC中点可求S△BED=2,即可求阴影部分面积.
【解答】解:如图作GD⊥BE于G,作CF⊥AE于F,
∵∠AEB=∠DEC=90°,
∴∠GED+∠DEF=90°,∠DEF+∠CEF=90°,
∴∠DEG=∠CEF且DE=EC,∠DGE=∠CFE=90°,
∴△GDE≌△FCE(AAS),
∴DG=CF;
∵S△BED=BE×DG,S△ACE=AE×CF且AE=BE,DG=CF,
∴S△BED=S△AEC;
∵D是BC中点,
∴S△BDE=S△DEC=×2×2=2,
∴S阴影部分=2+2=4.
故答案为:4.
三、解答题(本题共5小题,共46分)
19.(8分)如图,在平面直角坐标系中有一个△ABC,点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 9 .
【分析】(1)根据关于y轴对称的点的坐标特点画出△A1B1C1即可;
(2)利用矩形的面积减去三个顶点上三角形的面积即可.
【解答】解:(1)如图所示;
(2)S△ABC=4×5﹣×2×4﹣×3×3﹣×1×5
=20﹣4﹣﹣
=9.
故答案为:9.
20.(8分)如图:已知点A、E、F、B在一条直线上,AE=BF,CF=DE,AC=BD,求证:GE=GF.
【分析】由条件可先求得AF=BE,则可证得△ACF≌△BDE,可证得∠GEF=∠GFE,可证得GE=GF.
【解答】证明:
∵AF=BE,
∴AF+EF=BE+EF,
即AF=BE.
在△ACF和△BDE中,
∴△ACF≌△BDE(SSS),
∴∠GEF=∠GFE,
∴GE=GF.
21.(8分)如图,已知:△ABC中,AB边上的垂直平分线DE交AB于D,交AC于E,△BCE的周长为16cm,△ABC的周长为24cm,求AD的长度.
【分析】根据线段垂直平分线的性质得到EA=EB,AD=AB,根据三角形的周长公式计算,得到答案.
【解答】解:∵DE是AB边上的垂直平分线,
∴EA=EB,AD=AB,
∵△BCE的周长为16cm,
∴BC+CE+BE=BC+CE+EA=BC+AC=16cm,
∵△ABC的周长为24cm,
∴BC+AC+AB=24cm,
∴AB=24﹣16=8cm,
∴AD=AB=4cm.
22.(10分)如图,在△ABC中,AB=AC,点D在AB边上且点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)连接CD,若CD=CB,求∠B的度数.
【分析】(1)作线段AC的垂直平分线交AB于点D,点D即为所求.
(2)根据等腰三角形的性质和三角形的内角和解答即可.
【解答】解:(1)如图,点D即为所求.
(2)由(1)可知DE垂直平分AC,
∴AD=CD,
∴∠A=∠ACD,
设∠A=x,
∴∠ACD=x,
∴∠BDC=∠A+∠ACD=2x,
∵CD=CB,
∴∠B=∠BDC=2x,
∵AB=AC,
∴∠ACB=∠B=2x,
∵∠A+∠B+∠ACB=180°,
即x+2x+2x=180°,
解得:x=36,
∴∠B=2x=72°.
23.(12分)如图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
(1)求∠AEB的度数.
(2)试证明AE=BE+2CM.
【分析】(1)根据等腰直角三角形的性质得到CA=CB,CD=CE,∠CDE=∠CED=45°,求出∠ADC=135°,利用SAS定理证明△ADC≌△BEC,可得∠BEC=∠ADC=135°,即可求解;
(2)根据等腰三角形的性质、直角三角形的性质得到DE=2CM,结合图形证明即可.
【解答】解:(1)∵∠ACB=∠DCE=90°,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,即∠ACD=∠BCE,
∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠CDE=∠CED=45°,
∴∠ADC=135°,
在△ADC和△BEC中,
,
∴△ADC≌△BEC(SAS);
∴∠BEC=∠ADC=135°,
∴∠AEB=135°﹣45°=90°;
(2)∵△ADC≌△BEC,
∴BE=AD,
∵△DCE为等腰直角三角形,CM为△DCE中DE边上的高,
∴DE=2CM,
∴AE=AD+DE=BE+2CM.
一、选择题:(本大题10小题,每小题3分,共30分)
1.下列四个地铁标志中,是轴对称图形的是( )
A. B. C. D.
2.以下各组线段为边,能组成三角形的是( )
A.1cm,2cm,3cm B.1cm,3cm,5cm
C.2cm,3cm,4cm D.2cm,4cm,6cm
3.在平面直角坐标系中,点A关于x轴的对称点为A1(3,﹣2),则点A的坐标为( )
A.(3,2) B.(﹣3,﹣2) C.(3,﹣2) D.(﹣3、7)
4.一个多边形的每一个外角都等于36°,则这个多边形的边数n等于( )
A.8 B.10 C.12 D.14
5.三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的( )
A.三条中线的交点 B.三边垂直平分线的交点
C.三条高的交点 D.三条角平分线的交点
6.如图,已知△ABC的3条边和3个角,则能判断和△ABC全等的是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
7.如图,AD是△ABC的外角∠EAC的平分线,AD∥BC,∠B=32°,则∠C的度数是( )
A.64° B.32° C.30° D.40°
8.如图,△ABC中,AB=6,AC=9,BD、CD分别平分∠ABC,∠ACB过点D作直线平行于BC,分别交AB、AC于E、F,则△AEF的周长为( )
A.12 B.13 C.14 D.15
9.如图,已知∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C,EG⊥OA于点G,若EC=3,则OF长度是( )
A.3 B.4 C.5 D.6
10.如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段EF的长为( )
A. B. C.4 D.
二、填空题:(本大题8小题,每小题3分,共24分)
11.七边形的内角和是 .
12.等腰三角形的两边长分别是3和7,则其周长为 .
13.如图,在△ABC中,AB=AC,∠C=30°,DA⊥BA于点A,若CD=4cm,则BD= .
14.如图,在△ABC中,∠A=65°,∠B=45°,BC的垂直平分线分别交AB、BC于D、E,则∠ACD= .
15.如图所示,在直角坐标系中,△OBC的顶点O(0,0),B(﹣6,0),且∠OCB=90°,OC=BC,则点C关于y轴对称点C′的坐标是 .
16.如图,小亮从A点出发,沿直线前进15米后向左转30°,再沿直线前进15米,又向左转30°,…照这样走下去,他第一次回到出发地A点时,一共走了 米.
17.在平面直角坐标系中,点A(2,0),B(0,4),求点C,使以点B、O、C为顶点的三角形与△ABO全等,则点C的坐标为 .
18.如图,在△ABC中,AB=AC,点D是BC的中点,点E是△ABC内一点,若∠AEB=∠CED=90°,AE=BE,CE=DE=2,则图中阴影部分的面积等于 .
三、解答题(本题共5小题,共46分)
19.(8分)如图,在平面直角坐标系中有一个△ABC,点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .
20.(8分)如图:已知点A、E、F、B在一条直线上,AE=BF,CF=DE,AC=BD,求证:GE=GF.
21.(8分)如图,已知:△ABC中,AB边上的垂直平分线DE交AB于D,交AC于E,△BCE的周长为16cm,△ABC的周长为24cm,求AD的长度.
22.(10分)如图,在△ABC中,AB=AC,点D在AB边上且点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)连接CD,若CD=CB,求∠B的度数.
23.(12分)如图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
(1)求∠AEB的度数.
(2)试证明AE=BE+2CM.
2020-2021学年安徽省淮南市田家庵区八年级(上)期中数学试卷
参考答案与试题解析
一、选择题:(本大题10小题,每小题3分,共30分)
1.下列四个地铁标志中,是轴对称图形的是( )
A. B. C. D.
【分析】直接利用轴对称图形的定义得出答案.
【解答】解:A、不是轴对称图形,不合题意;
B、是轴对称图形,符合题意;
C、不是轴对称图形,不合题意;
D、不是轴对称图形,不合题意.
故选:B.
2.以下各组线段为边,能组成三角形的是( )
A.1cm,2cm,3cm B.1cm,3cm,5cm
C.2cm,3cm,4cm D.2cm,4cm,6cm
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【解答】解:根据三角形的三边关系,知
A、1+2=3,不能组成三角形;
B、1+3<5,不能组成三角形;
C、2+3>4,能够组成三角形;
D、2+4=6,不能组成三角形.
故选:C.
3.在平面直角坐标系中,点A关于x轴的对称点为A1(3,﹣2),则点A的坐标为( )
A.(3,2) B.(﹣3,﹣2) C.(3,﹣2) D.(﹣3、7)
【分析】利用关于x轴的对称点的坐标特点进行解答即可.
【解答】解:∵点A关于x轴的对称点为A1(3,﹣2),
∴点A的坐标为(3,2),
故选:A.
4.一个多边形的每一个外角都等于36°,则这个多边形的边数n等于( )
A.8 B.10 C.12 D.14
【分析】多边形的外角和是固定的360°,依此可以求出多边形的边数.
【解答】解:∵一个多边形的每一个外角都等于36°,
∴多边形的边数为360°÷36°=10.
故选:B.
5.三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的( )
A.三条中线的交点 B.三边垂直平分线的交点
C.三条高的交点 D.三条角平分线的交点
【分析】根据线段垂直平分线的性质:线段垂直平分线上任意一点,到线段两端点的距离相等可得答案.
【解答】解:三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的三边垂直平分线的交点,
故选:B.
6.如图,已知△ABC的3条边和3个角,则能判断和△ABC全等的是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
【分析】首先观察图形,然后根据三角形全等的判定方法(AAS与SAS),即可求得答案.
【解答】解:如图:
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SAS);
在△ABC和△MNK中,
,
∴△ABC≌△MNK(AAS).
∴甲、乙、丙三个三角形中和△ABC全等的图形是:乙或丙.
故选:B.
7.如图,AD是△ABC的外角∠EAC的平分线,AD∥BC,∠B=32°,则∠C的度数是( )
A.64° B.32° C.30° D.40°
【分析】根据平行线的性质求出∠EAD,根据角平分线的定义得到∠EAC=2∠EAD=64°,根据三角形的外角性质计算即可.
【解答】解:∵AD∥BC,
∴∠EAD=∠B=32°,
∵AD是△ABC的外角∠EAC的平分线,
∴∠EAC=2∠EAD=64°,
∵∠EAC是△ABC的外角,
∴∠C=∠EAC﹣∠B=64°﹣32°=32°,
故选:B.
8.如图,△ABC中,AB=6,AC=9,BD、CD分别平分∠ABC,∠ACB过点D作直线平行于BC,分别交AB、AC于E、F,则△AEF的周长为( )
A.12 B.13 C.14 D.15
【分析】根据平行线的性质得到∠EDB=∠DBC,∠FDC=∠DCB,根据角平分线的性质得到∠EBD=∠DBC,∠FCD=∠DCB,等量代换得到∠EDB=∠EBD,∠FDC=∠FCD,于是得到ED=EB,FD=FC,即可得到结果.
【解答】解:∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB,
∵△ABC中,∠ABC和∠ACB的平分线相交于点D,
∴∠EBD=∠DBC,∠FCD=∠DCB,
∴∠EDB=∠EBD,∠FDC=∠FCD,
∴ED=EB,FD=FC,
∵AB=6,AC=9,
∴△AEF的周长为:AE+EF+AF=AE+ED+FD+AF=AE+EB+FC+AF=AB+AC=6+9=15.
故选:D.
9.如图,已知∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C,EG⊥OA于点G,若EC=3,则OF长度是( )
A.3 B.4 C.5 D.6
【分析】根据角平分线的性质得到EG的长度,再根据平行线的性质得到∠OEF=∠COE=15°,然后利用三角形的外角和内角的关系求出∠EFG=30°,利用30°角所对的直角边是斜边的一半,即可得到EF的长,进而得出OF的长.
【解答】解:∵∠AOE=∠BOE=15°,EC⊥OB于点C,EG⊥OA于点G,
∴CE=EG=3,
∵EF∥OB,
∴∠COE=∠OEF=15°
∴∠EFG=15°+15°=30°,∠EOF=∠OEF,
∴OF=EF=2EG=2×3=6.
故选:D.
10.如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段EF的长为( )
A. B. C.4 D.
【分析】根据翻折的性质可知角ECF为45度,根据等腰直角三角形的性质和三角形的面积即可求解.
【解答】解:根据两次翻折可知:
∠ACE=∠DCE,∠BCF=∠DCF,CE⊥AD,
∵∠ACB=90°,
∴∠ECF=∠ECD+∠FCD=∠ACB=45°,
∴∠EFC=45°,
∴EF=CE,
∵S△ABC=AC•BC=AB•CE,
∴5CE=3×4,CE=.
∴EF=.
故选:B.
二、填空题:(本大题8小题,每小题3分,共24分)
11.七边形的内角和是 900° .
【分析】由n边形的内角和是:180°(n﹣2),将n=7代入即可求得答案.
【解答】解:七边形的内角和是:180°×(7﹣2)=900°.
故答案为:900°.
12.等腰三角形的两边长分别是3和7,则其周长为 17 .
【分析】因为边为3和7,没明确是底边还是腰,所以有两种情况,需要分类讨论.
【解答】解:分两种情况:
当3为底时,其它两边都为7,3、7、7可以构成三角形,周长为17;
当3为腰时,其它两边为3和7,3+3=6<7,所以不能构成三角形,故舍去,
所以等腰三角形的周长为17.
故答案为:17.
13.如图,在△ABC中,AB=AC,∠C=30°,DA⊥BA于点A,若CD=4cm,则BD= 8cm .
【分析】根据等腰三角形的性质求出∠B=∠C=30°,根据三角形内角和定理求出∠BAC,求出∠DAC=∠C=30°,求出AD=CD=4cm,根据含30°角的直角三角形的性质求出即可.
【解答】解:∵在△ABC中,AB=AC,∠C=30°,
∴∠B=∠C=30°,
∴∠BAC=180°﹣∠C﹣∠B=120°,
∵DA⊥AB,
∴∠BAD=90°,
∴∠DAC=120°﹣90°=30°,
∴∠C=∠DAC=30°,
∵CD=4cm,
∴AD=CD=4cm,
在Rt△BAD中,∠BAD=90°,AD=4cm,∠B=30°,
∴BD=2AD=8cm,
故答案为:8cm.
14.如图,在△ABC中,∠A=65°,∠B=45°,BC的垂直平分线分别交AB、BC于D、E,则∠ACD= 25° .
【分析】在△ABC中,∠A=65°,∠B=45°,根据三角形内角和定理可得∠ACB=70°,再由线段垂直平分线的性质可得DB=DC,根据等边对等角得出∠DCB=∠B=45°,然后根据∠ACD=∠ACB﹣∠DCB,计算即可求解.
【解答】解:在△ABC中,∵∠A=65°,∠B=45°,
∴∠ACB=180°﹣∠A﹣∠B=70°,
∵DE是BC的垂直平分线,
∴DB=DC,
∴∠DCB=∠B=45°,
∴∠ACD=∠ACB﹣∠DCB=70°﹣45°=25°.
故答案为25°.
15.如图所示,在直角坐标系中,△OBC的顶点O(0,0),B(﹣6,0),且∠OCB=90°,OC=BC,则点C关于y轴对称点C′的坐标是 (3,3) .
【分析】过点C作CD⊥OB于D,根据等腰直角三角形的性质可得CD=OD=OB,从而求出点C的坐标,再根据关于y轴对称的点,纵坐标相同,横坐标互为相反数求解即可.
【解答】解:如图,过点C作CD⊥OB于D,
∵∠OCB=90°,OC=BC,
∴△BOC是等腰直角三角形,
∴CD=OD=OB,
∵O(0,0),B(﹣6,0),
∴OB=6,
∴CD=OD=×6=3,
∴点C的坐标为(﹣3,3),
∴点C关于y轴对称点C′的坐标是(3,3).
故答案为:(3,3).
16.如图,小亮从A点出发,沿直线前进15米后向左转30°,再沿直线前进15米,又向左转30°,…照这样走下去,他第一次回到出发地A点时,一共走了 180 米.
【分析】由题意可知小亮所走的路线为一个正多边形,根据多边形的外角和即可求出答案.
【解答】解:∵360÷30=12,
∴他需要走12次才会回到原来的起点,即一共走了15×12=180(米).
故答案为:180.
17.在平面直角坐标系中,点A(2,0),B(0,4),求点C,使以点B、O、C为顶点的三角形与△ABO全等,则点C的坐标为 (﹣2,0)或(2,4)或(﹣2,4) .
【分析】由条件可知BO为两三角形的公共边,且△ABO为直角三角形,当△ABO和△BCO全等时,则可知△BCO为直角三角形,且有CO=AO可BC=AO,可得出C点的坐标.
【解答】解:∵点A(2,0),B(0,4),
∴AO=2,且△ABO为直角三角形,
当△ABO和△BCO全等时,则可知△BCO为直角三角形,且有公共边BO,
∴CO=AO或BC=AO,
当CO=AO时,则C点坐标为(﹣2,0);
当BC=AO时,则BC=2,且BC⊥OB,
∴C点坐标为(2,4)或(﹣2,4);
综上可知点C的坐为(﹣2,0)或(2,4)或(﹣2,4),
故答案为:(﹣2,0)或(2,4)或(﹣2,4).
18.如图,在△ABC中,AB=AC,点D是BC的中点,点E是△ABC内一点,若∠AEB=∠CED=90°,AE=BE,CE=DE=2,则图中阴影部分的面积等于 4 .
【分析】作GD⊥BE于G,作CF⊥AE于F,可证△DEG≌△CEF可得DG=CF,则S△BDE=S△AEC,由D是BC中点可求S△BED=2,即可求阴影部分面积.
【解答】解:如图作GD⊥BE于G,作CF⊥AE于F,
∵∠AEB=∠DEC=90°,
∴∠GED+∠DEF=90°,∠DEF+∠CEF=90°,
∴∠DEG=∠CEF且DE=EC,∠DGE=∠CFE=90°,
∴△GDE≌△FCE(AAS),
∴DG=CF;
∵S△BED=BE×DG,S△ACE=AE×CF且AE=BE,DG=CF,
∴S△BED=S△AEC;
∵D是BC中点,
∴S△BDE=S△DEC=×2×2=2,
∴S阴影部分=2+2=4.
故答案为:4.
三、解答题(本题共5小题,共46分)
19.(8分)如图,在平面直角坐标系中有一个△ABC,点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 9 .
【分析】(1)根据关于y轴对称的点的坐标特点画出△A1B1C1即可;
(2)利用矩形的面积减去三个顶点上三角形的面积即可.
【解答】解:(1)如图所示;
(2)S△ABC=4×5﹣×2×4﹣×3×3﹣×1×5
=20﹣4﹣﹣
=9.
故答案为:9.
20.(8分)如图:已知点A、E、F、B在一条直线上,AE=BF,CF=DE,AC=BD,求证:GE=GF.
【分析】由条件可先求得AF=BE,则可证得△ACF≌△BDE,可证得∠GEF=∠GFE,可证得GE=GF.
【解答】证明:
∵AF=BE,
∴AF+EF=BE+EF,
即AF=BE.
在△ACF和△BDE中,
∴△ACF≌△BDE(SSS),
∴∠GEF=∠GFE,
∴GE=GF.
21.(8分)如图,已知:△ABC中,AB边上的垂直平分线DE交AB于D,交AC于E,△BCE的周长为16cm,△ABC的周长为24cm,求AD的长度.
【分析】根据线段垂直平分线的性质得到EA=EB,AD=AB,根据三角形的周长公式计算,得到答案.
【解答】解:∵DE是AB边上的垂直平分线,
∴EA=EB,AD=AB,
∵△BCE的周长为16cm,
∴BC+CE+BE=BC+CE+EA=BC+AC=16cm,
∵△ABC的周长为24cm,
∴BC+AC+AB=24cm,
∴AB=24﹣16=8cm,
∴AD=AB=4cm.
22.(10分)如图,在△ABC中,AB=AC,点D在AB边上且点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)连接CD,若CD=CB,求∠B的度数.
【分析】(1)作线段AC的垂直平分线交AB于点D,点D即为所求.
(2)根据等腰三角形的性质和三角形的内角和解答即可.
【解答】解:(1)如图,点D即为所求.
(2)由(1)可知DE垂直平分AC,
∴AD=CD,
∴∠A=∠ACD,
设∠A=x,
∴∠ACD=x,
∴∠BDC=∠A+∠ACD=2x,
∵CD=CB,
∴∠B=∠BDC=2x,
∵AB=AC,
∴∠ACB=∠B=2x,
∵∠A+∠B+∠ACB=180°,
即x+2x+2x=180°,
解得:x=36,
∴∠B=2x=72°.
23.(12分)如图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
(1)求∠AEB的度数.
(2)试证明AE=BE+2CM.
【分析】(1)根据等腰直角三角形的性质得到CA=CB,CD=CE,∠CDE=∠CED=45°,求出∠ADC=135°,利用SAS定理证明△ADC≌△BEC,可得∠BEC=∠ADC=135°,即可求解;
(2)根据等腰三角形的性质、直角三角形的性质得到DE=2CM,结合图形证明即可.
【解答】解:(1)∵∠ACB=∠DCE=90°,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,即∠ACD=∠BCE,
∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠CDE=∠CED=45°,
∴∠ADC=135°,
在△ADC和△BEC中,
,
∴△ADC≌△BEC(SAS);
∴∠BEC=∠ADC=135°,
∴∠AEB=135°﹣45°=90°;
(2)∵△ADC≌△BEC,
∴BE=AD,
∵△DCE为等腰直角三角形,CM为△DCE中DE边上的高,
∴DE=2CM,
∴AE=AD+DE=BE+2CM.
相关资料
更多








