






所属成套资源:九年级数学上册 全一册课件(打包28套)(新版)新人教版
数学人教版22.1.1 二次函数课文配套课件ppt
展开这是一份数学人教版22.1.1 二次函数课文配套课件ppt,共16页。PPT课件主要包含了y=-x2+2x+3等内容,欢迎下载使用。
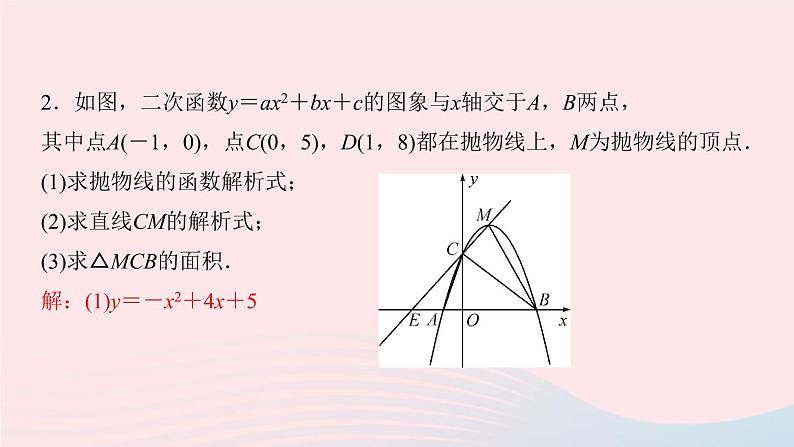
2.如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A(-1,0),点C(0,5),D(1,8)都在抛物线上,M为抛物线的顶点.(1)求抛物线的函数解析式;(2)求直线CM的解析式;(3)求△MCB的面积.解:(1)y=-x2+4x+5
3.已知一个二次函数,当x=1时,y有最大值8,其图象的形状、开口方向与抛物线y=-2x2相同,则这个二次函数的解析式是( )A.y=-2x2-x+3 B.y=-2x2+4C.y=-2x2+4x+8 D.y=-2x2+4x+6
4.已知某二次函数的最大值为2,图象的顶点在直线y=x+1上,并且图象经过点(2,1),求二次函数的解析式.解:∵函数的最大值是2,则此函数顶点的纵坐标是2,又顶点在y=x+1上,∴2=x+1,即x=1,∴顶点坐标为(1,2),设此函数的解析式是y=a(x-1)2+2,再把(2,1)代入函数中可得a(2-1)2+2=1,解得a=-1,故函数解析式是y=-(x-1)2+2,即y=-x2+2x+1
5.已知二次函数y=ax2+bx+c的x与y的部分对应值如下表:(1)求此二次函数的解析式;(2)画出此函数图象;(3)结合函数图象,写出当-4<x≤1时y的取值范围.解:(1)由表知,抛物线的顶点坐标为(-1,4),设y=a(x+1)2+4,把(0,3)代入得a(0+1)2+4=3,解得a=-1,∴抛物线的解析式为y=-(x+1)2+4,即y=-x2-2x+3 (2)图象略 (3)-5<y≤4
6.已知一个二次函数的图象经过点A(-1,0),B(3,0)和C(0,-3)三点;(1)求此二次函数的解析式;(2)对于实数m,点M(m,-5)是否在这个二次函数的图象上?说明理由.解:(1)设二次函数的解析式为y=a(x+1)(x-3),由于二次函数的图象经过C(0,-3),则有-3=a(0+1)(0-3),解得a=1,∴二次函数的解析式为y=(x+1)(x-3),即y=x2-2x-3 (2)由(1)可知y=x2-2x-3=(x-1)2-4,则y的最小值为-4>-5,因此无论m取何值,点M都不在这个二次函数的图象上
7.已知抛物线在x轴上截得的线段长是4,对称轴是x=-1,且过点(-2,-6),求该抛物线的解析式.解:∵抛物线的对称轴为x=-1,在x轴上截得的线段长为4,∴抛物线与x轴的交点坐标为(-3,0),(1,0),设抛物线解析式为y=a(x+3)(x-1),把(-2,-6)代入得a(-2+3)(-2-1)=-6,解得a=2,∴抛物线解析式为y=2(x+3)(x-1),即y=2x2+4x-6
8.已知y=x2+bx+c的图象向右平移2个单位长度,再向下平移3个单位长度,得到的图象对应的函数解析式为y=x2-2x-3.(1)b=___,c=___;(2)求原函数图象的顶点坐标;(3)求两个图象顶点之间的距离.
9.如图,已知抛物线y=-x2+bx+c的对称轴为直线x=1,且与x轴的一个交点为(3,0),那么它对应的函数解析式是________________.
相关课件
这是一份初中数学人教版九年级上册22.1.1 二次函数作业ppt课件,共13页。
这是一份人教版九年级上册22.1.1 二次函数习题课件ppt,共19页。
这是一份人教版九年级上册22.1.4 二次函数y=ax2+bx+c的图象和性质获奖ppt课件,共15页。PPT课件主要包含了待定系数法,探究归纳,对称性,①已知任意三点坐标,已知条件,所选方法等内容,欢迎下载使用。













