全面的北师大版数学八年级上册知识点总结

这是一份数学八年级上册本册综合学案，共6页。学案主要包含了实数的概念及分类，实数的倒数，平方根，算术平方根有关计算，实数的运算，正比例函数和一次函数等内容，欢迎下载使用。
勾股定理


1、勾股定理


直角三角形两直角边a，b的平方和等于斜边c的平方，即a2 +b2=c2


2、勾股定理的逆定理


如果三角形的三边长a，b，c有关系，a2 +b2=c2那么这个三角形是直角三角形。


勾股数：满足a2 +b2=c2的三个正整数，称为勾股数。


常见的勾股数（3，4，5），（6，8，10），（5，12，13），（8，15，17），（7，24，25）


第二章 实数


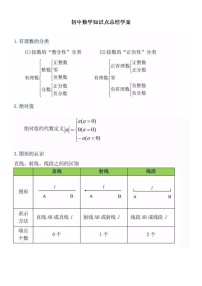
一、实数的概念及分类


1、实数的分类





整数（包括正整数，0，负整数）





有理数


实数 分数（包括正分数和负分数）








正无理数


无理数 无限不循环小数


负无理数


2、无理数：无限不循环小数叫做无理数。


在理解无理数时，要抓住“无限不循环”，归纳起来有三类：


（1）开方开不尽的数，如等；（2）化简后含有π的数，如+8等；


（3）有特定结构的数，如0.1010010001…等；注意：分数是有理数，不是分数。


二、实数的倒数、相反数和绝对值


1、相反数：实数与它的相反数是一对数（只有符号不同的两个数叫做互为相反数，零的相反数是零），从数轴上看，互为相反数的两个数所对应的点关于原点对称，如果a与b互为相反数，则有a+b=0，a=—b，反之亦成立。


2、绝对值：在数轴上，一个数所对应的点与原点的距离，叫做该数的绝对值。（|a|≥0）。零的绝对值是它本身，也可看成它的相反数，若|a|=a，则a≥0；若|a|=-a，则a≤0。


3、倒数：如果a与b互为倒数，则有ab=1，反之亦成立。倒数等于本身的数是1和-1。零没有倒数。


4、数轴：规定了原点、正方向和单位长度的直线叫做数轴（画数轴时，要注意上述规定的三要素缺一不可）。


三、平方根、算数平方根和立方根


1、算术平方根：一般地，如果一个正数x的平方等于a，即x2=a，那么这个正数x就叫做a的算术平方根。特别地，0的算术平方根是0。


表示方法：记作“”，读作根号a。算数平方根等于本身的数有0和1


性质：正数和零的算术平方根都只有一个，零的算术平方根是零。


2、平方根：一般地，如果一个数x的平方等于a，即x2=a，那么这个数x就叫做a的平方根（或二次方根）。


表示方法：正数a的平方根记做“”，读作“正、负根号a”。平方根等于本身的数有0和1.


性质：一个正数有两个平方根，它们互为相反数；零的平方根是零；负数没有平方根。


开平方：求一个数a的平方根的运算，叫做开平方。 注意的双重非负性：≥０，≥0


3、立方根


一般地，如果一个数x的立方等于a，即x3=a那么这个数x就叫做a 的立方根（或三次方根）。


表示方法：记作，性质：一个正数有一个正的立方根；一个负数有一个负的立方根；零的立方根是零。


1、实数比较大小：正数大于零，负数小于零，正数大于一切负数；数轴上的两个点所表示的数，右边的总比左边的大；两个负数，绝对值大的反而小。


2、实数大小比较的几种常用方法


（1）数轴比较：在数轴上表示的两个数，右边的数总比左边的数大。


（2）求差比较：设a、b是实数，若a－b≥0 则a≥b，若a－b≦0 则a≦b


（3）求商比较法：设a、b是两正实数，a÷b≥1 则a≥b a÷b≤1 则a≤b


（4）绝对值比较法：设a、b是两负实数，则|a|≥|b| 则a≤b


（5）平方法：设a、b是两负实数，。a2 ≥b2则a≤b


五、算术平方根有关计算（二次根式）


1、含有二次根号“”；被开方数a必须是非负数。


2、运算结果若含有“”形式，必须是最简二次根式。


满足：（1）被开方数的因数是整数，因式是整式；（2）被开方数中不含能开得尽方的因数或因式


3、性质：


（1） （2）


（3）


（4） （5）=a


4、运算结果若含有“”形式，必须满足：（1）被开方数的因数是整数，因式是整式；（2）被开方数中不含能开得尽方的因数或因式。


六、实数的运算


（1）六种运算：加、减、乘、除、乘方、开方


（2）实数的运算顺序


先算乘方和开方，再算乘除，最后算加减，如果有括号，就先算括号里面的。


第三章 位置的确定


一、 在平面内，确定物体的位置一般需要两个数据。


二、 平面直角坐标系内点的坐标特征:


若P的坐标为(a,b)，则P到x轴距离为_______，到y轴距离为_______．


(1)坐标轴把平面分隔成四个象限。根据点所在位置填表


(2)坐标轴上的点不属于任何象限，它们的坐标特征：


eq \\ac(○,1)在x轴上的点______坐标为0; eq \\ac(○,2) 在y轴上的点______坐标为0;


(3)P(a,b)关于x轴、y轴、原点的对称点坐标特征


eq \\ac(○,1) 点P(a,b)关于x轴对称点P1_____________ ；


eq \\ac(○,2)点 P(a,b)关于y轴对称点P2_____________ ；


eq \\ac(○,3)点P(a,b)关于原点对称点P3_____________ 。


5.平行于x轴的直线上的点______坐标相同；平行于y轴的直线上的点_______坐标相同．


6.探索图形变换与坐标变化规律


(1)若两个图形关于x轴对称．则对应各点横坐标_________，纵坐标互为___________．


(2)若两个图形关于y轴对称，则对应各点纵坐标_________，横坐标互为___________．


第四章 一次函数


一、函数：


一般地，在某一变化过程中有两个变量x与y，如果给定一个x值，相应地就确定了一个y值，那么我们称y是x的函数，其中x是自变量，y是因变量。


二、自变量取值范围


使函数有意义的自变量的取值的全体，叫做自变量的取值范围。一般从整式（取全体实数），分式（分母不为0）、二次根式（被开方数为非负数）、实际意义几方面考虑。


三、函数的三种表示法：列表法，图像法，关系式法


四、正比例函数和一次函数


1、正比例函数和一次函数的概念


一般地，若两个变量x，y间的关系可以表示成y=kx+b（k，b为常数，k不等于0）的形式，则称y是x的一次函数（x为自变量，y为因变量）。


特别地，当一次函数y=kx+b中的b=0时（即y=kx）（k为常数，k不等于0），称y是x的正比例函数。


2、一次函数的图像:所有一次函数的图像都是一条直线。


3、一次函数的图像


4、一次函数、正比例函数图像的主要特征：


（1）一次函数y=kx+b（k、b为常数，k≠0）的图像是经过点（0，b），（，0）的直线；正比例函数y=kx的图像是经过原点（0，0）的直线。


（2）两条直线当k相同时，两直线平行，当b相同时，两直线交于y轴同一点（0，b）。


5、一次函数的性质


一般地，一次函数y=kx+b（k、b为常数，k≠0）有下列性质：


（1）当k>0时，y随x的增大而增大


（2）当k