

数学必修22.1 空间点、直线、平面之间的位置关系教案设计
展开§2.1.3 空间中直线与平面之间的位置关系
一、教材分析
空间中直线与平面之间的位置关系是立体几何中最重要的位置关系,直线与平面的相交和平行是本节的重点和难点.空间中直线与平面之间的位置关系是根据交点个数来定义的,要求学生在公理1的基础上会判断直线与平面之间的位置关系.本节重点是结合图形判断空间中直线与平面之间的位置关系.
二、教学目标
1.知识与技能
(1)了解空间中直线与平面的位置关系;
(2)培养学生的空间想象能力.
2.过程与方法
(1)学生通过观察与类比加深了对这些位置关系的理解、掌握;
(2)让学生利用已有的知识与经验归纳整理本节所学知识.
3.情感、态度与价值
让学生感受到掌握空间直线与平面关系的必要性,提高学生的学习兴趣.
三、教学重点与难点
正确判定直线与平面的位置关系.
四、课时安排
1课时
五、教学设计
(一)导入新课
思路1.(情境导入)
一支笔所在的直线与我们的课桌面所在的平面,可能有几个交点?可能有几种位置关系?
思路2.(事例导入)
观察长方体(图1),你能发现长方体ABCD—A′B′C′D′中,线段A′B所在的直线与长方体ABCD—A′B′C′D′的六个面所在平面有几种位置关系?
图1
(二)推进新课、新知探究、提出问题
①什么叫做直线在平面内?
②什么叫做直线与平面相交?
③什么叫做直线与平面平行?
④直线在平面外包括哪几种情况?
⑤用三种语言描述直线与平面之间的位置关系.
活动:教师提示、点拨从直线与平面的交点个数考虑,对回答正确的学生及时表扬.
讨论结果:①如果直线与平面有无数个公共点叫做直线在平面内.
②如果直线与平面有且只有一个公共点叫做直线与平面相交.
③如果直线与平面没有公共点叫做直线与平面平行.
④直线与平面相交或平行的情况统称为直线在平面外.
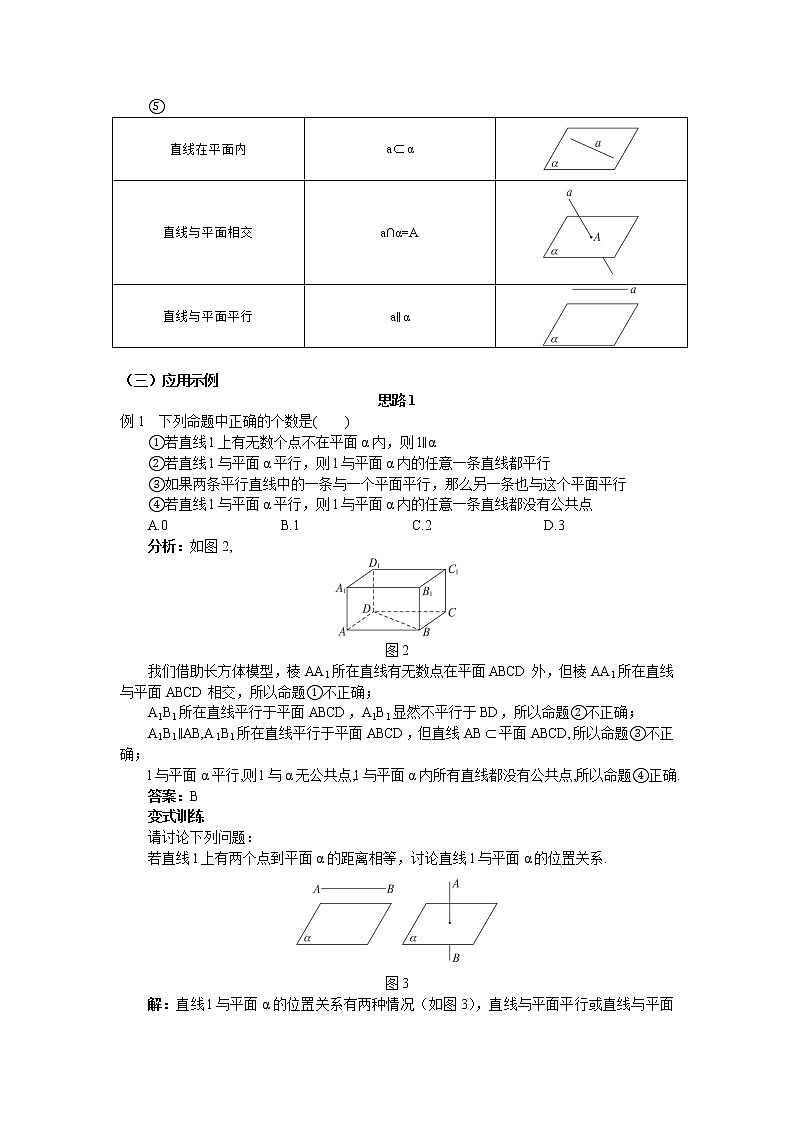
⑤
直线在平面内 | aα | |
直线与平面相交 | a∩α=A | |
直线与平面平行 | a∥α |
(三)应用示例
思路1
例1 下列命题中正确的个数是( )
①若直线l上有无数个点不在平面α内,则l∥α
②若直线l与平面α平行,则l与平面α内的任意一条直线都平行
③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行
④若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点
A.0 B.1 C.2 D.3
分析:如图2,
图2
我们借助长方体模型,棱AA1所在直线有无数点在平面ABCD外,但棱AA1所在直线与平面ABCD相交,所以命题①不正确;
A1B1所在直线平行于平面ABCD,A1B1显然不平行于BD,所以命题②不正确;
A1B1∥AB,A1B1所在直线平行于平面ABCD,但直线AB平面ABCD,所以命题③不正确;
l与平面α平行,则l与α无公共点,l与平面α内所有直线都没有公共点,所以命题④正确.
答案:B
变式训练
请讨论下列问题:
若直线l上有两个点到平面α的距离相等,讨论直线l与平面α的位置关系.
图3
解:直线l与平面α的位置关系有两种情况(如图3),直线与平面平行或直线与平面相交.
点评:判断直线与平面的位置关系要善于找出空间模型,结合图形来考虑,注意考虑问题要全面.
例2 已知一条直线与三条平行直线都相交,求证:这四条直线共面.
已知直线a∥b∥c,直线l∩a=A,l∩b=B,l∩c=C.
求证:l与a、b、c共面.
证明:如图4,∵a∥b,
图4
∴a、b确定一个平面,设为α.
∵l∩a=A,l∩b=B,∴A∈α,B∈α.
又∵A∈l,B∈l,∴ABα,即lα.
同理b、c确定一个平面β,lβ,
∴平面α与β都过两相交直线b与l.
∵两条相交直线确定一个平面,
∴α与β重合.故l与a、b、c共面.
变式训练
已知aα,bα,a∩b=A,P∈b,PQ∥a,
求证:PQα.
证明:∵PQ∥a,∴PQ、a确定一个平面,设为β.
∴P∈β,aβ,Pa.又P∈α,aα,Pa,
由推论1:过P、a有且只有一个平面,
∴α、β重合.∴PQα.
点评:证明两个平面重合是证明直线在平面内问题的重要方法.
思路2
例1 若两条相交直线中的一条在平面α内,讨论另一条直线与平面α的位置关系.
解:如图5,另一条直线与平面α的位置关系是在平面内或与平面相交.
图5
用符号语言表示为:若a∩b=A,bα,则aα或a∩α=A.
变式训练
若两条异面直线中的一条在平面α内,讨论另一条直线与平面α的位置关系.
分析:如图6,另一条直线与平面α的位置关系是与平面平行或与平面相交.
图6
用符号语言表示为:若a与b异面,aα,则b∥α或b∩α=A.
点评:判断直线与平面的位置关系要善于找出空间模型,结合图形来考虑,注意考虑问题要全面.
例2 若直线a不平行于平面α,且aα,则下列结论成立的是( )
A.α内的所有直线与a异面 B.α内的直线与a都相交
C.α内存在唯一的直线与a平行 D.α内不存在与a平行的直线
分析:如图7,若直线a不平行于平面α,且aα,则a与平面α相交.
图7
例如直线A′B与平面ABCD相交,直线AB、CD在平面ABCD内,直线AB与直线A′B相交,直线CD与直线A′B异面,所以A、B都不正确;平面ABCD内不存在与a平行的直线,所以应选D.
答案:D
变式训练
不在同一条直线上的三点A、B、C到平面α的距离相等,且Aα,给出以下三个命题:
①△ABC中至少有一条边平行于α;②△ABC中至多有两边平行于α;③△ABC中只可能有一条边与α相交.
其中真命题是_____________.
分析:如图8,三点A、B、C可能在α的同侧,也可能在α两侧,
图8
其中真命题是①.
答案:①
变式训练
若直线aα,则下列结论中成立的个数是( )
(1)α内的所有直线与a异面 (2)α内的直线与a都相交 (3)α内存在唯一的直线与a平行 (4)α内不存在与a平行的直线
A.0 B.1 C.2 D.3
分析:∵直线aα,∴a∥α或a∩α=A.
如图9,显然(1)(2)(3)(4)都有反例,所以应选A.
图9
答案:A
点评:判断一个命题是否正确要善于找出空间模型(长方体是常用空间模型),另外考虑问题要全面即注意发散思维.
(四)知能训练
已知α∩β=l,aα且aβ,bβ且bα,又a∩b=P.
求证:a与β相交,b与α相交.
证明:如图10,∵a∩b=P,
图10
∴P∈a,P∈b.
又bβ,∴P∈β.
∴a与β有公共点P,即a与β相交.
同理可证,b与α相交.
(五)拓展提升
过空间一点,能否作一个平面与两条异面直线都平行?
解:(1)如图11,
C′D′与BD是异面直线,可以过P点作一个平面与两异面直线C′D′、BD都平行.
如图12,
图11 图12 图13
显然,平面PQ是符合要求的平面.
(2)如图13,当点P与直线C′D′确定的平面和直线BD平行时,不存在过P点的平面与两异面直线C′D′、BD都平行.
点评:判断一个命题是否正确要善于找出空间模型(长方体是常用空间模型),另外考虑问题要全面即注意发散思维.
(六)课堂小结
本节主要学习直线与平面的位置关系,直线与平面的位置关系有三种:
①直线在平面内——有无数个公共点,
②直线与平面相交——有且只有一个公共点,
③直线与平面平行——没有公共点.
另外,空间想象能力的培养是本节的重点和难点.
(七)作业
课本习题2.1 A组7、8.
高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系公开课教案: 这是一份高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系公开课教案,共7页。教案主要包含了已知M等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系教案设计: 这是一份高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系教案设计,共3页。
高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系教案设计: 这是一份高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系教案设计,共3页。













