北京师范大学亚太实验学校2020-2021学年第一学期高三期中数学试卷含答案

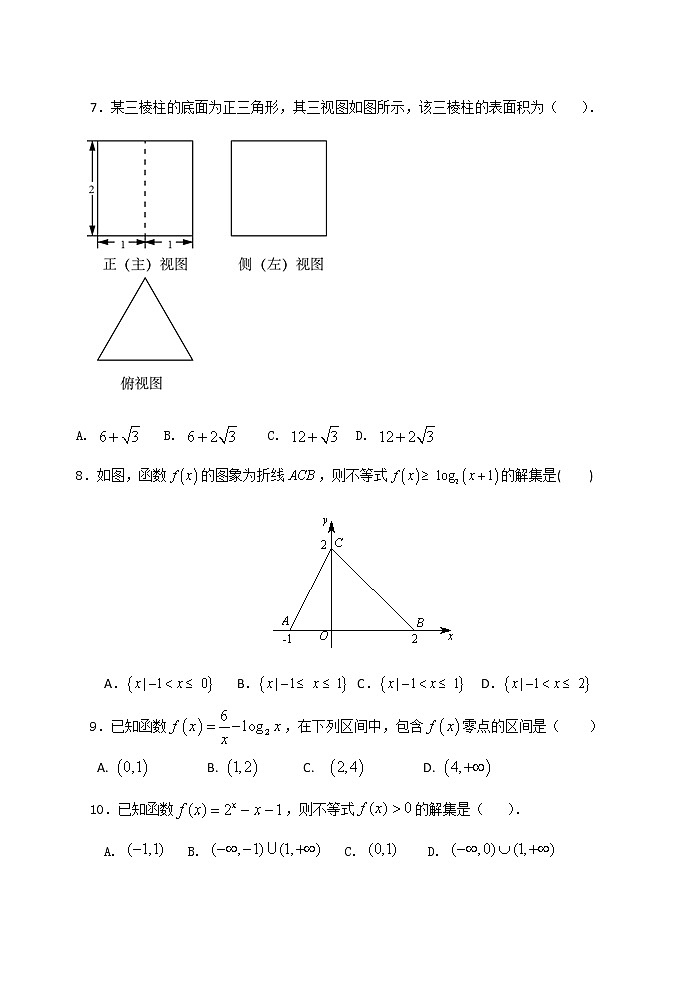
北京师范大学亚太实验学校2020-2021学年第一学期期中测试 高三数学        试卷说明: 本次考试满分150分,考试时间120分钟第一部分（选择题   共40分）一、    选择题:本大题共10小题,每小题4分，共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1. 已知集合，，则     (      )（A）  （B）（C） （D）2．已知集合P=｛x︱x2≤1｝,M=｛a｝.若P∪M=P,则a的取值范围是(   )（A）(-∞, -1] （B）[1, +∞） （C）[-1，1]  （D）（-∞，-1] ∪[1，+∞）3. 下列函数中，在区间（0，+）上单调递增的是  (      )（A） （B）y=   （C）    （D）4. 已知函数在区间上单调递增，那么区间可以是   (      )（A）   （B）       （C）      （D） 5. 命题””的否定为   (      )（A）                     （B） （C）                     （D） 66．已知函数，则    (       ) （A）是奇函数，且在R上是增函数         （B）是偶函数，且在R上是增函数 （C）是奇函数，且在R上是减函数         （D）是偶函数，且在R上是减函数    7．某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为（    ）．
A.    B.     C.  D. 8．如图，函数的图象为折线，则不等式的解集是(    )A．   B． C．  D．9．已知函数，在下列区间中，包含零点的区间是（    ）   A.         B.       C.          D. 10．已知函数，则不等式的解集是（    ）．A.    B.    C.     D.   第二部分（非选择题   共110分）二.填空题:本大题共5小题,每题5分,共25分，答案写在横线上.11. ，，三个数中最大数的是         ．12．函数的定义域是_____________________．13．已知{}是各项均为正的等比数列，为其前项和，若，，则公比____，____．14．已知向量，，若，则___________.15．李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为60元/盒、65元/盒、80元/盒、90元/盒．为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x元．每笔订单顾客网上支付成功后，李明会得到支付款的80%．①当x=10时，顾客一次购买草莓和西瓜各1盒，需要支付__________元；②在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x的最大值为__________．三.解答题:本大题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16（本小题满分14分）如图，在四棱锥P-ABCD中，PD=2AD,底面ABCD为正方形，M、N分别为AD、PD的中点。（1）求证：（2） 求直线PB与平面MNC所成角的正弦值                   17. （本小题满分14分）已知函数.（1）求的最小正周期； （2）若在区间上的最大值为，求的最小值.             18.（本小题14分）在中，，再从条件①、条件②这两个条件中选择一个作为己知，求：（Ⅰ）a的值：（Ⅱ）和的面积．条件①：；条件②：．注：如果选择条件①和条件②分别解答，按第一个解答计分．                          19.（本小题14分）已知{}是公比为q的无穷等比数列，其前n项和为Sn，满足是否存在正整数k,使得若存在，求k的最小值；若不存在，说明理由。从（1）q=2  ,  (2)    (3) q=-2 这三个条件中任选一个，补充在上面问题中并作答。注：如果选择多个条件分别解答，按第一个解答计分。                               20．（本小题14分）已知函数f（x）=（x+1）2﹣3alnx，a∈R．（1）求函数f（x）图象经过的定点坐标；（2）当a=1时，求曲线f（x）在点（1，f（1））处的切线方程及函数f（x）单调区间；（3）若对任意x∈[1，e]，f（x）≤4恒成立，求实数a的取值范围．                              21. （本小题15分）已知函数．（Ⅰ）求曲线的斜率为1的切线方程；（Ⅱ）当时，求证：；（Ⅲ）设，记在区间上的最大值为M（a），当M（a）最小时，求a的值．                         2020-2021学年北京师范大学亚太实验学校高三数学参考答案一、 选择：1A 2,C 3,A 4,D 5,A,6,A,7,D,8,C.9,C,10,D二、填空11，    12， （-1，1）      13，    14，  -5   15，130，15三、解答题16解：（Ⅰ）因为分别为的中点， 所以．           …………… 2分                                   又因为平面，   …………… 3分                                     所以平面．      …………… 5分                                   （Ⅱ）如图建立空间直角坐标系．设，则，，，，，，                                                   ……………… 7分，．设平面的法向量为，则　即                         ……………… 10分令，则，．所以．            ……………… 12分设直线与平面所成角为，所以．　       　      ……………… 14分           17【解析】，所以的最小正周期为.    ……..6分（2）由（1）知.因为，所以.要使得在上的最大值为，即在上的最大值为1.所以，即.      …….12分所以的最小值为.  …….14分18．【详解】选择条件①（Ⅰ）    …….6分（Ⅱ）由正弦定理得：   ……..10分选择条件②（Ⅰ）正弦定理得：（Ⅱ）   …….14分19．解1：选择①                                                因为，所以．                              ……………… 4分所以公式给3分                       ………………9分令， 即．                          ……………… 12分所以使得的正整数的最小值为．           ……………… 14分           解2：选择②                                                           因为，所以．                             ……………… 4分．                           ……………… 9分因为，                                   ……………… 12分所以不存在满足条件的正整数.                         ……………… 14分 解3：选择③                                                 因为，所以．                               ……………… 4分所以．                        ……………… 9分令, 即，整理得．    ……………… 12分当为偶数时，原不等式无解；当为奇数时，原不等式等价于， 所以使得的正整数的最小值为．             ……………… 14分20．解：（1）当x=1时，ln1=0，所以f（1）=4，所以函数f（x）的图象无论a为何值都经过定点（1，4）。…….4分（2）当a=1时，f（x）=（x+1）2﹣3lnx．f（1）=4，，f'（1）=1，则切线方程为y﹣4=1×（x﹣1），即y=x+3．   ……8分在x∈（0，+∞）时，如果，即时，函数f（x）单调递增；如果，即时，函数f（x）单调递减．,,,,,,,,10分（3），x＞0．当a≤0时，f'（x）＞0，f（x）在[1，e]上单调递增．f（x）min=f（1）=4，f（x）≤4不恒成立．当a＞0时，设g（x）=2x2+2x﹣3a，x＞0．∵g（x）的对称轴为，g（0）=﹣3a＜0，∴g（x）在（0，+∞）上单调递增，且存在唯一x0∈（0，+∞），使得g（x0）=0．∴当x∈（0，x0）时，g（x）＜0，即f'（x）＜0，f（x）在（0，x0）上单调递减；∴当x∈（x0，+∞）时，g（x）＞0，即f'（x）＞0，f（x）在（x0，+∞）上单调递增．∴f（x）在[1，e]上的最大值f（x）max=max{f（1），f（e）}．∴，得（e+1）2﹣3a≤4，解得．……..14分21．解：（Ⅰ）由得．令，即，得或．又，，所以曲线的斜率为1的切线方程是与，即与．……6分（Ⅱ）令．由得．令得或．的情况如下：       所以的最小值为，最大值为．故，即． …….12分（Ⅲ）由（Ⅱ）知，当时，；当时，；当时，．综上，当最小时，．  …….15分。