2020年北师大版九上数学期末复习：《投影与视图》（含答案） 试卷

北师大版九上数学期末复习《投影与视图》

一、选择题

1.如果在同一时刻的阳光下，小莉的影子比小玉的影子长，那么在同一路灯下（    ）

A.小莉的影子比小玉的影子长

B.小莉的影子比小玉的影子短

C.小莉的影子与小玉的影子一样长

D.无法判断谁的影子长

2.某数学课外活动小组想利用树影测量树高，他们在同一时刻测得一身高为1.5 m的同学的影长为1.35 m，由于大树靠近一幢建筑物，因此树影的一部分落在建筑物上，如图，他们测得地面部分的影长为3.6 m，建筑物上的影长为1.8 m，则树的高度为(　　)

A.5.4 m          B.5.8 m          C.5.22 m            D.6.4 m

3.如图是滨河公园中的两个物体一天中四个不同时刻在太阳光的照射下落在地面上的影子，按照时间的先后顺序排列正确的是(　　)

A.③④①②        B.④③①②        C.④③②①      D.②④③①

4.用三个正方体，一个圆柱体，一个圆锥摆成如图所示的几何体，其主视图为(    )

5.下列几何体中，俯视图是圆的几何体是（　　）

A.   B.  C.   D.

6.如图，由6个相同的小正方体组合成一个立体图形，它的俯视图为(　　)

   A．  B．   C．  D．

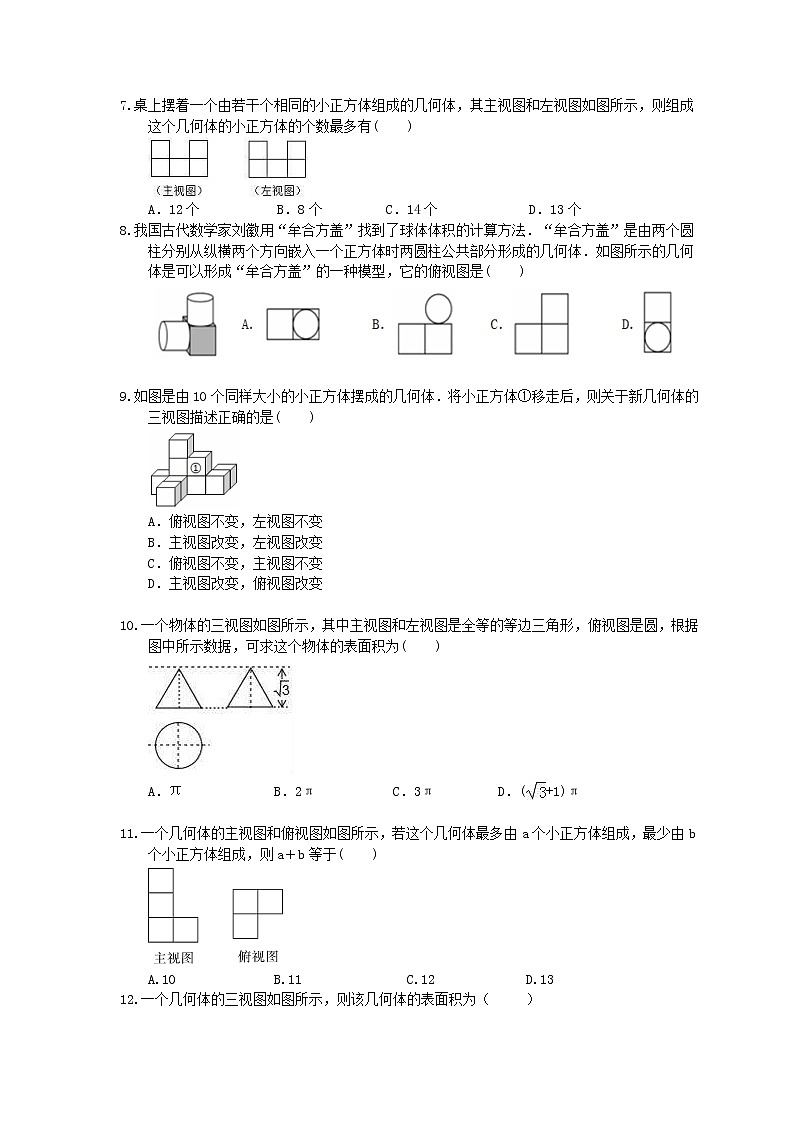
7.桌上摆着一个由若干个相同的小正方体组成的几何体，其主视图和左视图如图所示，则组成这个几何体的小正方体的个数最多有(　　)

A．12个      B．8个     C．14个       D．13个

8.我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法．“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体．如图所示的几何体是可以形成“牟合方盖”的一种模型，它的俯视图是(　　)

9.如图是由10个同样大小的小正方体摆成的几何体．将小正方体①移走后，则关于新几何体的三视图描述正确的是(　　)

A．俯视图不变，左视图不变

B．主视图改变，左视图改变

C．俯视图不变，主视图不变

D．主视图改变，俯视图改变

10.一个物体的三视图如图所示，其中主视图和左视图是全等的等边三角形，俯视图是圆，根据图中所示数据，可求这个物体的表面积为(　　)

A．π       B．2π      C．3π     D．(+1)π

11.一个几何体的主视图和俯视图如图所示，若这个几何体最多由a个小正方体组成，最少由b个小正方体组成，则a＋b等于(　　)

A.10              B.11               C.12             D.13

12.一个几何体的三视图如图所示，则该几何体的表面积为（     ）

A．4π        B．3π        C．2π+4             D．3π+4

二、填空题

13.如图是测得的两根木杆在同一时间的影子，它们是由_______形成的投影(填“太阳光”或“灯光”).

14.一个长方体的三视图如图所示，若其俯视图为正方形，则这个长方体的表面积为________.

15.对于下列说法：

①太阳光线可以看成平行光线，这样的光线形成的投影是平行投影；

②物体投影的长短在任何情况下，仅与物体的长短有关；

③物体的俯视图是光线垂直照射时，物体的投影；

④看书时人们之所以使用台灯，是因为台灯发出的光线是平行光线.

其中正确的是________.(把所有正确结论的序号都填上)

16.如图，晚上，小亮走在大街上.他发现：当他站在大街两边的两盏路灯之间，并且自己被两边路灯照在地上的两个影子成一直线时，自己右边的影子长为3米，左边的影子长为1.5米.又知自己身高1.8米，两盏路灯的高相同，两盏路灯之间的距离为12米，则路灯的高为__________米.

17.如图是一个长方体的三视图（单位：cm），根据图中数据计算这个长方体的体积是_________.

18.如图，小军、小珠之间的距离为2.7m，他们在同一盏路灯下的影长分别为1.8m，1.5m，已知小军、小珠的身高分别为1.8m，1.5m，则路灯的高为     m．

三、作图题

19.画图题：

①由大小相同的小立方块搭成的几何体如左图，请在右图的方格中画出该几何体的俯视图和左视图。

②用小立方体搭一几何体，使得它的俯视图和左视图与你在右图方格中所画的图一致，

则这样的几何体最少要_______个小立方块，最多要_______个小立方块。

四、解答题

20.如图是由两个长方体组合而成的一个立体图形的三视图，根据图中所示尺寸(单位：mm)，计算出这个立体图形的表面积.

21.如图，在路灯下，小明的身高如图中线段AB所示，他在地面上的影子如图中线段AC所示，小亮的身高如图中线段FG所示，路灯灯泡在线段DE上.

（1）请你确定灯泡所在的位置，并画出小亮在灯光下形成的影子.

（2）如果小明的身高AB=1.6m，他的影子长AC=1.4m，且他到路灯的距离AD=2.1m，求灯泡的高.

22.我国《道路交通安全法》第四十七条规定“机动车行经人行横道时，应当减速行驶；遇行人通过人行横道，应当停车让行”.如图：一辆汽车在一个十字路口遇到行人时刹车停下，汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°，如果斑马线的宽度是AB=3米，驾驶员与车头的距离是0.8米，这时汽车车头与斑马线的距离x是多少？

23.如图，小明家窗外有一堵围墙AB，由于围墙的遮挡，清晨太阳光恰好从窗户的最高点C射进房间的地板F处，中午太阳光恰好能从窗户的最低点D射进房间的地板E处，小明测得窗子距地面的高度OD=0.8m，窗高CD=1.2m，并测得OE=0.8m，OF=3m，求围墙AB的高度.

24.晚饭后，小聪和小军在社区广场散步，小聪问小军：“你有多高？”小军一时语塞.小聪思考片刻，提议用广场照明灯下的影长及地砖长来测量小军的身高.于是，两人在灯下沿直线NQ移动，如图，当小聪正好站在广场的A点(距N点5块地砖长)时，其影长AD恰好为1块地砖长；当小军正好站在广场的B点(距N点9块地砖长)时，其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成，小聪的身高AC为1.6米，MN⊥NQ，AC⊥NQ，BE⊥NQ.请你根据以上信息，求出小军身高BE的长(结果精确到0.01米).

参考答案

1.答案为：D　

2.答案为：B.

3.答案为：C

4.答案为：A；

5.答案为：A.

6.答案为：D

7.答案为：D

8.答案为：A.

9.答案为：A.

10.答案为：C．

11.答案为：C　

12.D

13.答案为：太阳光.　

14.答案为：66.

15.答案为：①

16.答案为：6.6.

17.答案为：24.

18.答案为：3m．

19.解：（1）如图：

  （2）5，7.

20.解：根据三视图可得：上面的长方体长4mm，高4mm，宽2mm，

下面的长方体长8 mm，宽6 mm，高2 mm，

∴立体图形的表面积是：

4×4×2＋4×2×2＋4×2＋6×2×2＋8×2×2＋6×8×2－4×2=200(mm2)

21.解：

22.解：如图所示：延长AB，

∵CD∥AB，

∴∠CAB=30°，∠CBF=60°，

∴∠BCA=60°﹣30°=30°，即∠BAC=∠BCA，

∴BC=AB=3m，

在Rt△BCF中，BC=3m，∠CBF=60°，

∴BF=0.5BC=1.5m，故x=BF﹣EF=1.5﹣0.8=0.7（m），

答：这时汽车车头与斑马线的距离x是0.7m.

23.解：延长OD，

∵DO⊥BF，

∴∠DOE=90°，

∵OD=0.8m，OE=0.8m，

∴∠DEB=45°，

∵AB⊥BF，

∴∠BAE=45°，

∴AB=BE，

设AB=EB=x m，

∵AB⊥BF，CO⊥BF，

∴AB∥CO，

∴△ABF∽△COF，

，解得：x=4.4.

经检验：x=4.4是原方程的解.

答：围墙AB的高度是4.4m.

24.解：