七年级上册期末专题复习08：第四章几何图形初步（提升卷）附答案解析

【七年级数学(上)期末专题复习】
专题08 第四章几何图形初步(提升卷)
(测试时间：60分钟 试卷总分：120分)
班级：________ 姓名：________ 得分：________
一、选择题(每小题3分，共30分)
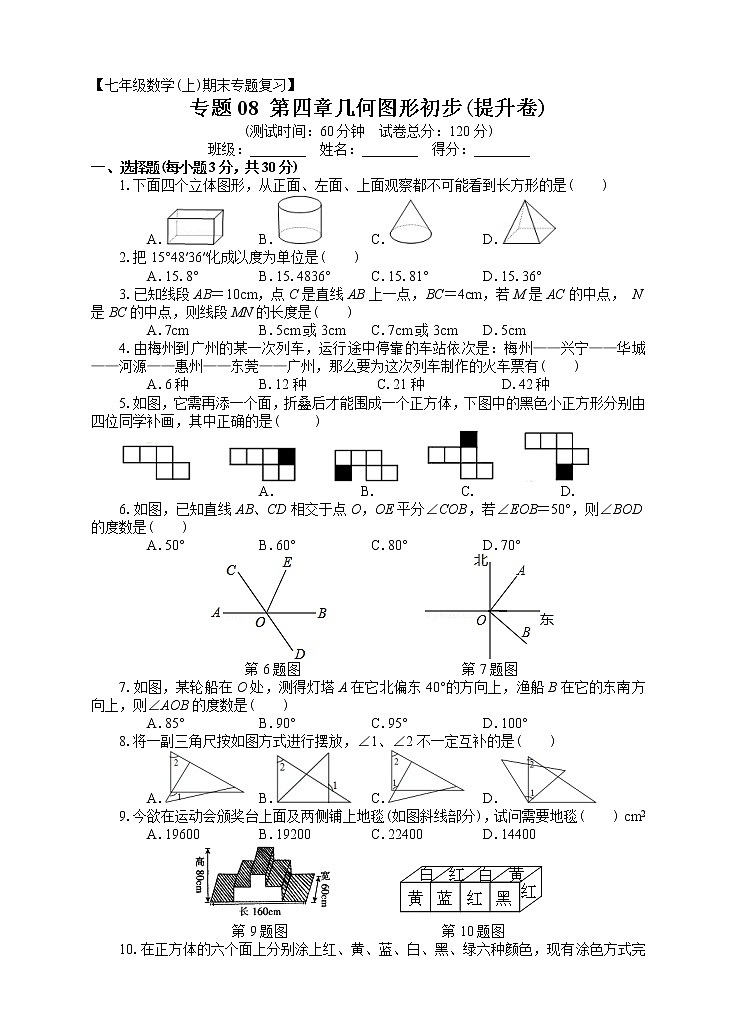
1.下面四个立体图形，从正面、左面、上面观察都不可能看到长方形的是( )
A. B. C. D.
2.把15°48′36″化成以度为单位是( )
A.15.8° B.15.4836° C.15.81° D.15.36°
3.已知线段AB＝10cm，点C是直线AB上一点，BC＝4cm，若M是AC的中点， N是BC的中点，则线段MN的长度是( )
A.7cm B.5cm或3cm C.7cm或3cm D.5cm
4.由梅州到广州的某一次列车，运行途中停靠的车站依次是：梅州——兴宁——华城——河源——惠州——东莞——广州，那么要为这次列车制作的火车票有( )
A.6种 B.12种 C.21种 D.42种
5.如图，它需再添一个面，折叠后才能围成一个正方体，下图中的黑色小正方形分别由四位同学补画，其中正确的是( )

A. B. C. D.
6.如图，已知直线AB、CD相交于点O，OE平分∠COB，若∠EOB＝50°，则∠BOD的度数是( )
A.50° B.60° C.80° D.70°

第6题图 第7题图
7.如图，某轮船在O处，测得灯塔A在它北偏东40°的方向上，渔船B在它的东南方向上，则∠AOB的度数是( )
A.85° B.90° C.95° D.100°
8.将一副三角尺按如图方式进行摆放，∠1、∠2不一定互补的是( )
A. B. C. D.
9.今欲在运动会颁奖台上面及两侧铺上地毯(如图斜线部分)，试问需要地毯( ) cm2
A.19600 B.19200 C.22400 D.14400

第9题图 第10题图
10.在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色，现有涂色方式完全相同的四个正方体，按照如图所示拼成一个长方体，那么涂黄、白两种颜色的面的对面分别涂有( )颜色.
A. 蓝、红 B. 蓝、黑 C. 蓝、绿 D. 绿、白
二、填空题(每小题3分，共30分)
11.若一个角的补角是这个角的余角的3倍，则这个角的度数为 .
12.一个棱锥的棱数是12，则这个棱锥的面数是 .
13.如图，直线AB，CD相交于点O，OE平分，若，则的度数是 .

第13题图 第14题图 第15题图
14.如图，C、D是线段AB上两点，若CB＝4cm，DB＝7cm，且D是AC中点，则AC的长 等于 cm.
15.如图，直线AB、CD相交于点O，∠BOD与∠BOE互为余角，∠BOE ＝18°，则∠AOC＝ °.
16.如图是以长为120cm，宽为80cm的长方形硬纸，在它的四个角处各剪去一个边长为20cm的正方形后，将其折叠成如图所示的无盖的长方体，则这个长方体的体积为 .

第16题图 第19题图
17.已知直线l上有三点A、B、C，且AB＝6，BC＝4，M、N分别是线段AB、BC的中点，则MN＝ .
18.对于线段的中点，有以下几种说法：①若AM＝MB，则M是AB的中点；②若AM＝MB＝AB，则M是AB的中点；③若AM＝AB，则M是AB的中点；④若A，M，B在一条直线上，且AM＝MB，则M是AB的中点.其中正确的是 .
19.有一个正方体的六个面上分别标有数字1、2、3、4、5、6，从三个不同的角度观察这个正方体所得到的结果如图所示，如果标有数字6的面所对面上的数字记为a，2的面所对面上数字记为b，那么a＋b的值为 .
20.下面左图是一个没有完全剪开的正方体，若再剪开一条棱，则得到的平面展开图可能是下面右图中六种图形中的 .(填写字母)

三、解答题(共60分)
21.(6分)计算：
(1)22°18′×5； (2)90°﹣57°23′27″.



22.(6分)如图，已知∠BOC＝2∠AOC，OD平分∠AOB，且∠COD＝20°，求∠AOB的度数.

23.(6分)用小立方块搭一个几何体，使它从正面和上面看到的形状如图所示，从上面看到形状中小正方形中的字母表示在该位置上小立方块的个数，请问：

(1)，各表示几？ 答：_____ ，_____；
(2)这个几何体最少由_____个小立方块搭成，最多由____个小立方块搭成；
(3)能搭出满足条件的几何体共有____种情况，其中从左面看这个几何体的形状图共有____种，请在所给网格图中画出其中的任意一种.
24.(6分)已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD、OE.
(1)如图①,当∠BOC＝70°时，求∠DOE的度数；
(2)如图②，当射线OC在∠AOB内绕点O旋转时，∠DOE的大小是否发生变化？若变化，说明理由；若不变，求∠DOE的度数.




25.(8分)已知一道路沿途5个车站A、B、C、D、E，它们之间的距离如图所示(km)

(1)求D、E两站之间的距离；
(2)如果a＝8，D为线段AE的中点，求b的值.




26.(8分)如图所示.

(1)若线段AB＝4cm，点C在线段AB上(如图①)，点M、N分别是线段AC、BC的中点，求线段MN长.
(2)若线段AB＝acm，点C在线段AB的延长线上(如图②)，点M、N分别是线段AC、BC的中点，你能猜想出MN的长度吗？请写出你的结论，并说明理由.





27.(10分)钟面角是指时钟的时针与分针所成的角.如图，图①、图②、图③三个钟面上的时刻分别记录了某中学的早晨上课时间7：30、中午放学时间11：50、下午放学时间17：00.
(1)分别写出图中钟面角的度数：∠1＝ °、∠2＝ °、∠3＝ °；
(2)在某个整点，钟面角可能会等于90°，写出可能的一个时刻为 ；
(3)请运用一元一次方程的知识解决问题：钟面上，在7：30～8：00之间，钟面角等于90°的时刻是多少？






28.(10分)已知点A在数轴上对应的数为a，点B对应的数为b，且，A、B之间的距离记作，
(1)求线段AB的长|AB|；
(2)设点P在数轴上对应的数为x，当|PA|－|PB|＝2时，求x的值；
(3)若点P在点A的左侧，M、N分别是PA、PB的中点，当点P在A的左侧移动时，下列两个结论：①|PM|＋|PN|的值不变；②|PN|－|PM|的值不变，其中只有一个结论正确，请判断出正确结论，并求其值.




参考答案
1.C
2.C
【解析】根据度、分、秒之间的换算关系求解.
解：15°48′36″，
＝15°＋48′＋(36÷60)′，
＝15°＋(48.6÷60)°，
＝15.81°.
故选C.
3.D.
【解析】分类讨论：(1)当点C在线段AB上时，则(2)当点C在线段AB的延长线上时，则综合上述情况，线段MN的长度是5cm.故选D.
4.D.
【解析】每两站点都要设火车票，所以从每一个城市出发到其他6个城市都有6种车票，运行途中停靠的车站依次是：梅州－－兴宁－－华城－－河源－－惠州－－东莞－－广州，共7个城市，所以要为这次列车制作的火车票有6×7＝42种.故选D.
5.C
【解析】根据正方体的展开图形可得只有C能够满足条件.
6.C
【解析】首先根据角平分线的性质可得∠EOB＝∠COE，进而得到∠COB的度数，再根据邻补角互补可算出∠BOD的度数.
解：∵OE平分∠COB，
∴∠EOB＝∠COE，
∵∠EOB＝50°，
∴∠COB＝100°，
∴∠BOD＝180°﹣100°＝80°.
故选：C.
7.C
【解析】根据方向角的定义以及角度的和差即可求解.
解：∠AOB＝180°﹣40°﹣45°＝95°.
故选C.
8.D
【解析】如果两个角的和等于180°(平角)，就说这两个角互为补角.即其中一个角是另一个角的补角，据此分别判断出每个选项中∠1＋∠2的度数和是不是180°，即可判断出它们是否一定互补.
解：如图1，，
∵∠2＋∠3＝90°，∠3＋∠4＝90°，
∴∠2＝∠4，
∵∠1＋∠4＝180°，
∴∠1＋∠2＝180°，
∴∠1、∠2互补.
如图2，，
∠2＝∠3，
∵∠1＋∠3＝180°，
∴∠1＋∠2＝180°，
∴∠1、∠2互补.
如图3，，
∵∠2＝60°，∠1＝30°＋90°＝120°，
∴∠1＋∠2＝180°，
∴∠1、∠2互补.
如图4，，
∵∠1＝90°，∠2＝60°，
∴∠1＋∠2＝90°＋60°＝150°，
∴∠1、∠2不互补.
故选：D.

9.B.
【解析】解：地毯总长：80×2＋160＝320(cm)，
320×60＝19200cm2，
故选B.
10.B
【解析】根据对应的性质可得：黄对蓝、白对黑、红对绿.
11.45°
【解析】解：设这个角是x，
则这个角的补角为180°－x，余角为90°－x，
所以3(90°－x)＝180°－x，
整理，可得2x＝90°，
解得：x＝45°，
即这个角的度数为45°.
12.7.
【解析】棱数是12，故多面体为六棱锥，可得多面体的面数为7.
解：因为一个棱锥的棱数是12，
可得多面体为六棱锥，
所以多面体的面数为7，
故答案为：7.
13.72°
【解析】根据∠AOB＝180°，∠AOE＝144°可得：∠BOE＝180°－144°＝36°，根据角平分线的性质可得：∠BOD＝2∠BOE＝2×36°＝72°，根据对顶角的性质可得：∠AOC＝∠BOD＝72°.
14.6
【解析】根据线段中点的性质可知：
由D是AC的中点，得AC＝2DC，再由CB＝4cm，DB＝7cm得CD＝BD－CB＝3cm，因此可得AC＝6cm.
15.72°
【解析】根据∠BOD与∠BOE互为余角，∠BOE＝18°可得：∠BOD＝72°，根据对顶角的性质可得：∠AOC＝∠BOD＝72°.
16.64000立方厘米.
【解析】要求这个长方体的体积，需要知道它的长、宽、高，由题意可知：长方体的长与宽即硬纸片长、宽分别减去小正方形两个边长，长方体的高即小正方形的边长，再根据长方体的体积(容积)公式：v＝abh，把数据代入公式解答.
解：(120﹣20×2)×(80﹣20×2)×20
＝80×40×20
＝64000(立方厘米)
答：这个长方体的体积是64000立方厘米.
故答案为：64000立方厘米.
17.5或1.
【解析】本题没有给出图形，在画图时，应考虑到A、B、C三点之间的位置关系的多种可能，再根据正确画出的图形解题.
解：①如图1：
∵M为AB的中点，AB＝6，
∴MB＝AB＝3，
∵N为BC在中点，AB＝4，
∴NB＝BC＝2，
∴MN＝MB＋NB＝5.
②如图2：
∵M为AB的中点，AB＝6，
∴MB＝AB＝3，
∵N为BC的中点，AB＝4，
∴NB＝BC＝2，
∴MN＝MB﹣NB＝1.
故答案为：5或1.

18.②④
【解析】因为点A，B，M要在一条直线上，且AM＝MB时，M是AB的中点，所以①错误；若AM＝MB＝AB，则M是AB的中点，所以②正确；因为点A，B，M要在一条直线上，且AM＝AB，则M是AB的中点，所以③错误，因为若A，M，B在一条直线上，且AM＝MB，则M是AM的中点，所以④正确；所以正确的有②④.
19.7
【解析】根据与1相邻的面的数字有2、3、4、6判断出1的对面数字是5，与4相邻的面的数字有1、3、5、6判断出4的对面数字是2，从而确定出3的对面数字是6，然后确定出a、b的值，相加即可.
解：由图可知，∵与1相邻的面的数字有2、3、4、6，
∴1的对面数字是5，
∵与4相邻的面的数字有1、3、5、6，
∴4的对面数字是2，
∴3的对面数字是6，
∵标有数字6的面所对面上的数字记为a，2的面所对面上数字记为b，
∴a＝3，b＝4，
∴a＋b＝3＋4＝7.
故答案为：7.
20.A、B、E
【解析】根据正方体的展开图的画法可得：只有A、B、E符合条件.
21.(1)111°30′；(2)32°36′33″.
【解析】(1)先让度、分、秒分别乘5，秒的结果若满60，转换为1分；分的结果若满60，则转化为1度.相同单位相加，满60，向前进1即可.
(2)此题是度数的减法运算，注意1°＝60′即可.
解：(1)22°18′×5＝110°90′＝111°30′；
(2)90°﹣57°23′27″＝32°36′33″.
22.120°
【解析】设∠AOC＝x，则∠BOC＝2x，∠AOB＝3x.先由角平分线的定义得出∠AOD＝，再根据∠AOD﹣∠AOC＝∠COD＝20°，列出关于x的方程，解方程求出x的值，进而得到∠AOB的度数.
解：设∠AOC＝x，则∠BOC＝2∠AOC＝2x，∠AOB＝∠BOC＋∠AOC＝3x.
∵OD平分∠AOB，
∴∠AOD＝∠AOB＝.
又∵∠AOD﹣∠AOC＝∠COD＝20°，
∴﹣x＝20°，
解得x＝40°，
∴∠AOB＝3x＝120°.
23.(1)b＝1，c＝3；(2)9，11；(3)详见解析.
【解析】(1)由主视图可知，第二列小立方体的个数均为1，第3列小正方体的个数为3，那么b＝1，c＝3；(2)第一列小立方体的个数最多为2＋2＋2，最少为2＋1＋1，那么加上其他两列小立方体的个数即可；(3)能搭出满足条件的几何体共有7种情况，其中从左面看这个几何体的形状图共有4种，请在所给网格图中画出其中的任意一种即可.
解：(1)b＝1，c＝3；
(2)最少由_9___个小立方块搭成，最多由11_个小立方块搭成。
(3)能搭出满足条件的几何体共有7种情况，其中从左面看这个几何体的形状图共有4种，请在所给网格图中画出其中的任意一种.下图供参考：

24.(1)45°；(2)，不变，∠DOE＝45°
【解析】根据角平分线的性质可以得到∠BOC＝2∠COE，∠AOC＝2∠DOC，再根据∠AOC＋∠BOC＝90°就可以得出∠DOE的度数.
解：(1)∵OD、OE分别平分∠AOC和∠BOC.
∴∠COE＝∠COB＝35°, ∠COD＝∠AOC＝15°
∴∠DOE＝∠DOC＋∠EOC＝ 45°
(2) ∠DOE的大小不变等于45°
理由：∠DOE＝ ∠DOC＋∠COE＝∠A OC＋∠COB＝(∠AOC＋∠ COB)＝∠AOB＝45°
25.(1)D、E两站之间的距离是a＋2b；(2)b＝4.
【解析】(1)根据线段的和差，可得答案；
(2)根据线段中点的性质，可得关于b的方程，根据解方程，可得答案.
解：(1)由线段的和差，得
DE＝CE﹣CD＝(3a﹣b)﹣(2a﹣3b)＝a＋2b；
D、E两站之间的距离是a＋2b；
(2)D为线段AE的中点，得
AD＝DE，即a＋b＋2a﹣3b＝a＋2b，
a＝2b＝8，b＝4.
26.(1)2cm；(2)acm.
【解析】(1)先根据点M，N分别是AC、BC的中点得出MC＝AC，NC＝BC，再根据MN＝MC＋NC即可得出结论；
(2)先根据点M，N分别是AC、BC的中点得出MC＝AC，NC＝BC，再根据MN＝MC﹣NC即可得出结论；
解：(1)∵点M，N分别是AC、BC的中点，AB＝4cm，
∴MC＝AC，NC＝BC，
∴MN＝MC＋NC＝(AC＋BC)＝AB＝×4cm＝2cm；
(2)MN＝acm，
理由是：∵点M，N分别是AC、BC的中点，AB＝acm，
∴MC＝AC，NC＝BC，
∴MN＝MC﹣NC＝(AC﹣BC)＝AB＝×acm＝acm.
27.(1)45°；55°150°.(2)3：00或者9：00.(3)钟面上，在7：30～8：00之间，钟面角等于90°的时刻是7：54.
【解析】(1)由钟面有12大格可知每个大格度数为＝30°，结合时针走一大格等于一小时等于分针走12大格的关系可找出结论；
(2)整点是最好找的，由分针指向12，可得知时针指向3或者9时，钟面角为90°；
(3)设经过x分钟钟面角为90°，由时针和分针转动的速度的关系可得出结论.
解：(1)由图①知，此时钟面角为(1＋)＝45°；
由图②知，此时钟面角为(1＋)＝55°；
由图③知，此时钟面角为(5﹣0)＝150°.
故答案为：45°；55°150°.
(2)当3：00时，时针指向3，分针指向12，此时钟面角为90°，
当9：00时，时针指向9，分针指向12，此时钟面角为90°
故答案为3：00或者9：00.
(3)设从7：30开始经过x分钟后钟面角为90°，此时：
分针转过的角度为＝6x°，时针转过的角度为分针的，即，
|6x°﹣(45°＋)|＝90°
解得x＝，或x＝﹣(舍去)
30＋＝＝54，
所以，钟面上，在7：30～8：00之间，钟面角等于90°的时刻是7：54.
28.(1)5；(2)；(3)第②个结论正确，|PN|－|PM|＝.
【解析】(1)应用非负数的性质得，a＋4＝0，b－1＝0,解得a和b的值，进而求得|AB|的值；
(2)应考虑到A、B、P三点之间的位置关系的多种可能解题；
(3)当P在A的左侧移动时，设点P对应的数为x，列式求出|PN|－|PM|的值即可.
解：(1)由题意得a＋4＝0，b－1＝0，解得a＝－4，b＝1，所以|AB|＝1－(－4)＝5；
(2)当P在点A左侧时，|PA|－|PB|＝－(|PB|－|PA|)＝－|AB|＝－5≠2，
当P在点B右侧时，|PA|－|PB|＝|AB|＝5≠2，
∴上述两种情况的点P不存在，
当P在A、B之间时，|PA|＝|x－(－4)|＝x＋4，|PB|＝|x－1|＝1－x，
∵|PA|－|PB|＝2，∴(x＋4)－(1－x)＝2，∴x＝；
，，