人教版新课标A必修2第四章 圆与方程综合与测试优秀单元测试练习题

第三章 圆与方程单元测试卷（巅峰版）

一、选择题 共12小题，每小题5分，共60分。在每小题列出的四个选项中，选出符合题目要求的一项。

1．直线与圆相切，则实数等于（ ）

A．或 B．或 C．或 D．或

【答案】C

【解析】圆的方程即为（ ，圆心 到直线的距离等于半径 或者 ，故选C．

2．若直线与圆有两个不同的公共点，那么点与圆的位置关系是（    ）．

A．点在圆外 B．点在圆内 C．点在圆上 D．不能确定

【答案】A

【解析】因为直线与圆有两个公共点，所以有，

即，因为点与的圆心的距离为，圆的半径为2，

所以点在圆外.故选:A．

3．在空间直角坐标系中，设点是点关于坐标原点的对称点，则(　 )

A．     B．     C．     D．

【答案】C

【解析】[来源:学.科.网]∵点关于坐标原点的对称点B（-1，3，﹣），

∴=（-2，6，﹣），∴|AB|==8．故选：C．

4．已知点P（1，1）及圆C：，点M，N在圆C上，若PM⊥PN，则|MN|的取值范围为（　）

A．     B．

C．     D．

【答案】A

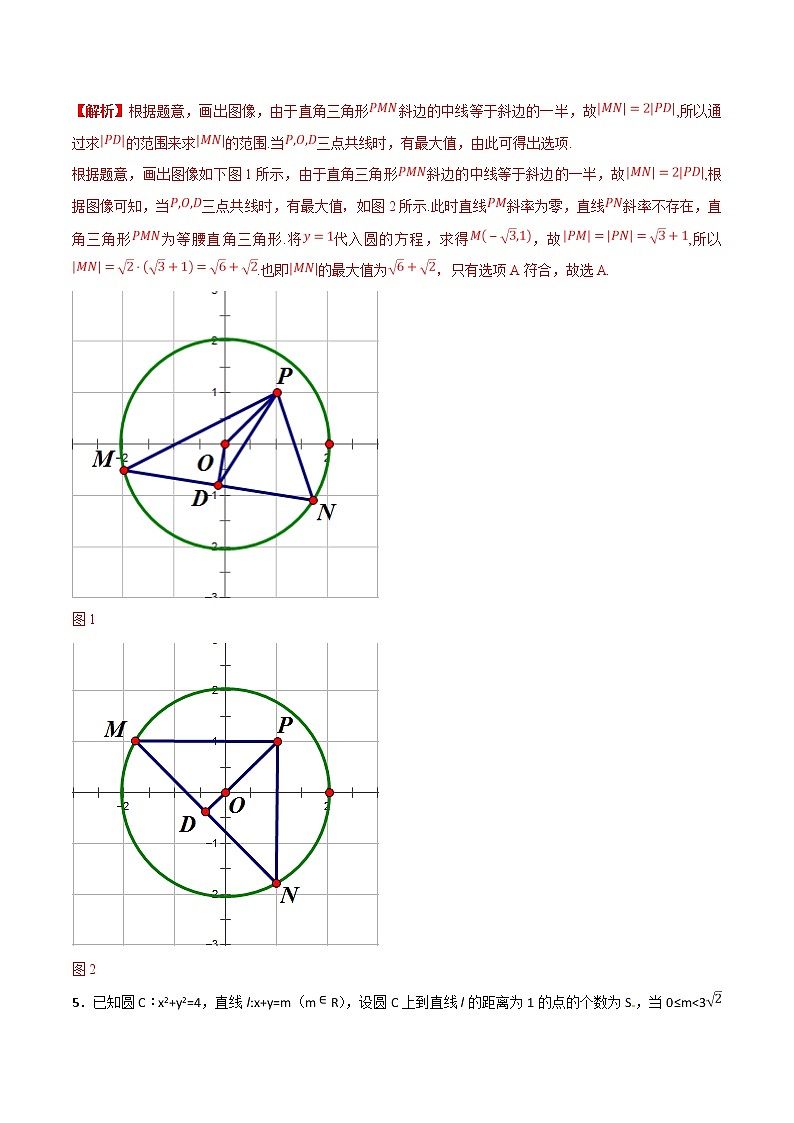
【解析】根据题意，画出图像，由于直角三角形斜边的中线等于斜边的一半，故,所以通过求的范围来求的范围.当三点共线时，有最大值，由此可得出选项.

根据题意，画出图像如下图1所示，由于直角三角形斜边的中线等于斜边的一半，故,根据图像可知，当三点共线时，有最大值，如图2所示.此时直线斜率为零，直线斜率不存在，直角三角形为等腰直角三角形.将代入圆的方程，求得，故,所以.也即的最大值为，只有选项A符合，故选A.

图1

图2

5．已知圆C：x2+y2=4，直线l:x+y=m（mR），设圆C上到直线l的距离为1的点的个数为S，当0≤m<3时，则S的可能取值共有（   ）

A． 2种    B． 3种    C． 4种    D． 5种

【答案】B

【解析】因为圆C上到直线l的距离为，

所以当时，圆C上到直线l的距离为1的点的个数为3；

当时，圆C上到直线l的距离为1的点的个数为2；

当时，圆C上到直线l的距离为1的点的个数为4；

因此S的可能取值共有3种，选B.

6．已知圆与直线相交于两点，为圆上的一点，的中点在线段上，且，则圆的半径为（  ）

A．     B．     C．     D．

【答案】C[来源:学科网ZXXK]

7．过点的直线将圆分成两段弧,当其中的劣弧最短时,直线的方程是(　  　)

A．     B．     C．     D．

【答案】C

【解析】由条件知M点在圆内，故当劣弧最短时, 应与圆心与M点的连线垂直,

设圆心为,则，

故直线的斜率，

的方程为，即.[来源:学科网ZXXK]

故选C.

8．“”是“为圆方程”的（    ）

A．充分不必要条件 B．必要不充分条件

C．充要条件 D．既不充分又不必要条件

【答案】A

【解析】方程表示圆需满足或，所以“”是“为圆方程”的充分不必要条件，故选：A.

9、若无论实数a取何值时，直线ax＋y＋a＋1＝0与圆x2＋y2－2x－2y＋b＝0都相交，则实数b的取值范围为(　　)

A．(－∞，2)  B．(2，＋∞)

C．(－∞，－6)  D．(－6，＋∞)

【答案】　C  

【解析】(1)∵x2＋y2－2x－2y＋b＝0表示圆，∴8－4b＞0，即b＜2.∵直线ax＋y＋a＋1＝0过定点(－1，－1)，∴点(－1，－1)在圆x2＋y2－2x－2y＋b＝0的内部，∴6＋b＜0，解得b＜－6，∴b的取值范围是(－∞，－6)．故选C.

10、若圆x2＋y2＝r2(r＞0)上恒有4个点到直线x－y－2＝0的距离为1，则实数r的取值范围是(　　)

A．(＋1，＋∞)  B．(－1，＋1)

C．(0，－1)  D．(0，＋1)

【答案】 A

【解析】计算得圆心到直线l的距离为＝＞1，如图，直线l：x－y－2＝0与圆相交，l1，l2与l平行，且与直线l的距离为1，故可以看出，圆的半径应该大于圆心到直线l2的距离＋1.

11、若圆O1：x2＋y2＝5与圆O2：(x＋m)2＋y2＝20相交于A，B两点，且两圆在点A处的切线互相垂直，则线段AB的长度是(　　)

A．3  B．4

C．2  D．8

【答案】B　

【解析】连接O1A，O2A，由于⊙O1与⊙O2在点A处的切线互相垂直，因此O1A⊥O2A，所以|O1O2|2＝|O1A|2＋|O2A|2，即m2＝5＋20＝25，设AB交x轴于点C.在Rt△O1AO2中，

sin∠AO2O1＝，∴在Rt△ACO2中，|AC|＝|AO2|·sin∠AO2O1＝2×＝2，∴|AB|＝2|AC|＝4.故选B.

12、已知圆C1：x2＋y2＋4ax＋4a2－4＝0和圆C2：x2＋y2－2by＋b2－1＝0只有一条公切线，若a，b∈R且ab≠0，则＋的最小值为(     )

A. 3       B. 8      C. 4       D. 9

【答案】D

【解析】　由题设中可知两圆相内切，其中C1(－2a，0)，r1＝2；C2(0，b)，r2＝1，故|C1C2|＝，由题设可知＝2－1，即a2＋4b2＝1，则＋＝(a2＋4b2)＝5＋＋≥5＋4＝9.当且仅当a2＝2b2时等号成立．故选D.

二、填空题  共4小题，每小题5分，共20分。

13．若不论取何值，直线恒过定点，则这个定点的坐标为__________．

【答案】

【解析】

直线的方程可化为：，

由的任意性可得：，

解得：，

故定点的坐标为．

故答案为：。

14．已知点为圆外一点，若圆上存在一点，使得，则正数的取值范围是____________．

【答案】

【解析】

由圆C：（x﹣a）2+（y﹣a）2=2a2，

得圆心为C（a，a），半径r=a，（a＞0），

∴PC=，

设过P的一条切线与圆的切点是T，则TC=a，

∴当Q为切点时，∠CPQ最大，

∵圆C上存在点Q使得∠CPQ=30°，

∴满足≥sin30°，

即≥，整理可得3a2+2a﹣2≥0，解得a≥或a≤，

又≤1，即≤1，解得a≤1，

又点 P（0，2）为圆C：（x﹣a）2+（y﹣a）2=2a2外一点，

∴a2+（2﹣a）2＞2a2，解得a＜1，

∵a＞0，∴综上可得≤a＜1．

故答案为：．

15．已知圆，直线，下面五个命题：

①对任意实数与，直线和圆有公共点；

②存在实数与，直线和圆相切；

③存在实数与，直线和圆相离；

④对任意实数，必存在实数，使得直线与和圆相切；

⑤对任意实数，必存在实数，使得直线与和圆相切.

其中真命题的代号是______________________（写出所有真命题的代号）.

【答案】①②④

【解析】

直线恒过定点，

将代入，等式成立，即圆过定点，

据此可知：对任意实数与，直线和圆有公共点；存在实数与，直线和圆相切；不存在实数与，直线和圆相离；说法①②正确，说法③错误；

对任意实数，必存在实数，使得直线与和圆相切；说法④正确；

当时，圆的方程为：，此时不存在实数，使得直线与和圆相切，即说法⑤错误.

综上可得：真命题的代号是①②④.

16．在平面直角坐标系中，已知圆，，动点在直线上，过点分别作圆的切线，切点分别为，若满足的点有且只有两个，则实数的取值范围是________．

【答案】.

【解析】

由题意O(0,0),O1(4,0).设P(x,y)，则[来源:学科网ZXXK]

∵PB=2PA，，

∴(x−4)2+y2=4(x2+y2)，

∴x2+y2+=0，

圆心坐标为,半径为，

∵动点P在直线x+y−b=0上，满足PB=2PA的点P有且只有两个，

∴直线与圆x2+y2+=0相交，

∴圆心到直线的距离，

∴，

即实数的取值范围是.

三、解答题  共6小题，共70分。解答应写出文字说明，演算步骤或证明过程。

17.已知两点O(0,0),A(6,0),圆C以线段OA为直径,

(1)求圆C的方程;

(2)若直线l1的方程为x-2y+4=0,直线l2平行于l1,且被圆C截得的弦MN的长是4,求直线l2的方程.

【解析】 (1)依题意知:圆C的半径r==3,

圆心坐标为(3,0),故圆C的方程为(x-3)2+y2=9.

(2)∵直线l2平行于l1,直线l1的方程为x-2y+4=0,

∴设直线l2的方程为x-2y+C=0,

又∵ 弦长MN=4,圆的半径为3,故圆心C到直线l2的距离d=,

∴|3+C|=5,得C=2或C=-8,

∴直线l2的方程为x-2y+2=0或x-2y-8=0.

18．已知△ABC的三个顶点分别为A(－3,0)，B(2,1)，C(－2,3)，求：

(1)BC边所在直线的方程；

(2)BC边的垂直平分线所在直线方程．

【答案】（1）.(2).

19．已知的三个顶点坐标分别是，， ．

（1）求边的高所在直线的点斜式方程；

（2）求边上的中线所在直线的一般式方程．

【答案】（1）；（2）.

【解析】

（1）边上的高所在的直线为直线为垂足，由已知得： ，

而，

而，所以直线的方程为 

（2）边上的中线所在的直线为直线为中点，

由已知， 得： ，

而，得： ，[来源:学科网ZXXK]

所以直线的方程为，即.

20．已知三个点，，，圆为的外接圆．

（）求圆的方程．

（）设直线，与圆交于，两点，且，求的值．

【答案】(1) (2)

（）圆心到直线的距离，

∵弦长，

∴有勾股定理得，

即，

解得．

21．如图，某海面上有、、三个小岛（面积大小忽略不计），岛在岛的北偏东方向距岛千米处，岛在岛的正东方向距岛20千米处.以为坐标原点，的正东方向为轴的正方向，1千米为单位长度，建立平面直角坐标系.圆经过、、三点.

（1）求圆的方程；

（2）若圆区域内有未知暗礁，现有一船D在岛的南偏西30°方向距岛40千米处，正沿着北偏东行驶，若不改变方向，试问该船有没有触礁的危险？

【解析】（1）如图所示，、，

设过、、三点的圆的方程为，

得：，

解得，，，

故所以圆的方程为，

圆心为，半径，

（2）该船初始位置为点，则，

且该船航线所在直线的斜率为1，

故该船航行方向为直线：，

由于圆心到直线的距离，

故该船有触礁的危险.

22．已知圆C:，直线 ，过的一条动直线与直线相交于N，与圆C相交于P,Q两点，M是PQ中点．

(1)当时，求直线的方程；

(2)设，试问是否为定值,若为定值,请求出的值；若不为定值，请说明理由．

【答案】（1）或  （2）

【解析】

(1) 当直线与轴垂直时,

易知符合题意; 

当直线与轴不垂直时,

设直线的方程为,

由于,

所以由,

解得. 

故直线的方程为或 

(2)当与轴垂直时,易得,,又则

,故. 即 

当的斜率存在时,设直线的方程为,代入圆的方程得

.

则 ,

即,  .

又由得,

则.

故. [来源:Zxxk.Com]

综上,的值为定值,且   

 解法二（几何法）:

连结,延长交于点，计算CA斜率知.又于,

故△∽△.于是有.

由得

故