宁夏银川一中2021届高三第四次月考 数学试卷（文）（含答案）

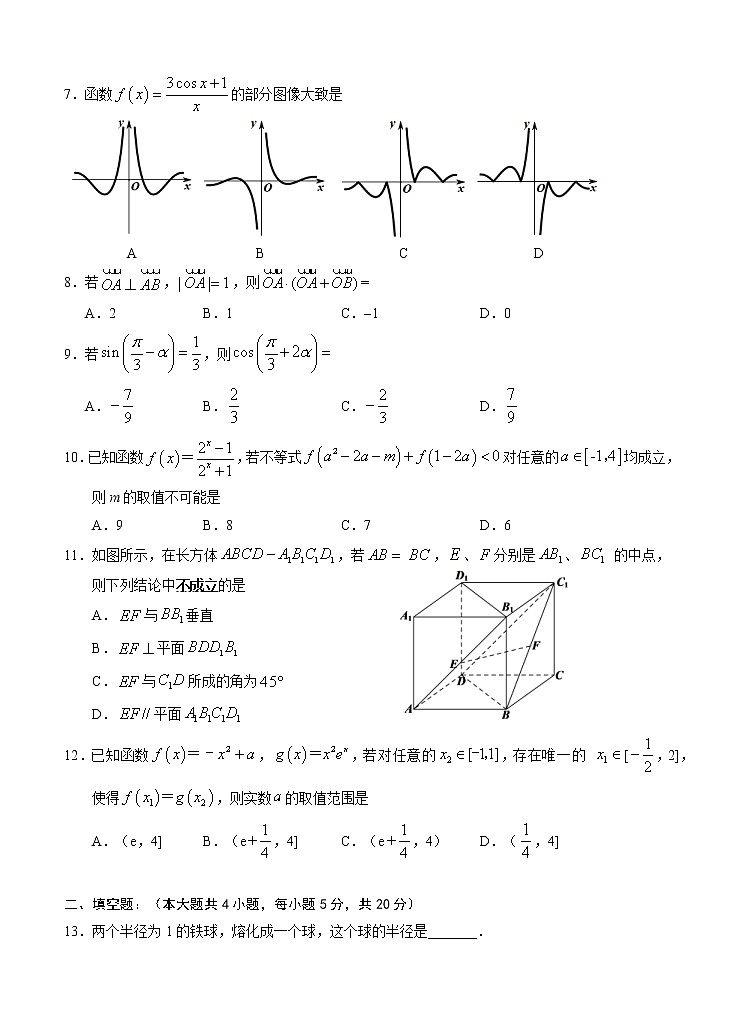
银川一中2021届高三年级第四次月考文 科 数 学 注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。2．作答时，务必将答案写在答题卡上。写在本试卷及草稿纸上无效。3．考试结束后，将本试卷和答题卡一并交回。 一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设全集，，则的值为A．2 B．8 C．2或8 D．－2或82．已知命题“”为真，“”为真，则下列说法正确的是A．真真 B．假真 C．真假 D．假假3．已知为虚数单位，复数，则A． B．2 C． D．4．已知函数 (且的图像恒过定点，点在幂函数 的图像上，则A．  B． C．1 D．25．已知将函数的图象向右平移个单位长度后所得的图象关于 轴对称，则的值可能为A． B． C． D．6．在等差数列中，若，且它的前项和有最小值，则当时，的最小值为A．14 B．15 C．16 D．177．函数的部分图像大致是     A                 B                   C                  D8．若，，则=A．2 B．1 C．1 D．09．若，则A． B． C． D．10．已知函数，若不等式对任意的均成立，则m的取值不可能是A．9 B．8 C．7 D．611．如图所示，在长方体，若，、分别是、 的中点，则下列结论中不成立的是A．与垂直 B．平面C．与所成的角为 D．平面12．已知函数，，若对任意的，存在唯一的 [，2]，使得，则实数的取值范围是A．（e，4] B．（e，4] C．（e，4） D．（，4] 二、填空题：（本大题共4小题，每小题5分，共20分）13．两个半径为1的铁球，熔化成一个球，这个球的半径是_______．14．已知向量，，若A，B，C三点共线，则实数_____．15．在三棱柱中，底面ABC，是正三角形，若，则该三棱柱外接球的表面积为_______.16．如图，在平面上作边长为的正方形，以所作正方形的一边为斜边向外作等腰直角三角形，然后以该等腰直角三角形的一条直角边为边向外作正方形，再以新的正方形的一边为斜边向外作等腰直角三角形，如此这般的作正方形和等腰直角三角形，不断地持续下去，求前n个正方形与前n个等腰直角三角形的面积之和__________.三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。(一)必考题：(共60分)17．(12分)已知数列为递增的等差数列，其中，且成等比数列．（1）求的通项公式；（2）设记数列的前n项和为．18．(12分)已如图所示，在四棱锥中，底面是矩形，平面，M，N分别是AB，PC的中点，．(1)求证：平面(2)求证：平面PCD．19．(12分)已知，，分别为内角，，的对边，若同时满足下列四个条件中的三个：①；②；③；④.（1）满足三角形可解的序号组合有哪些?（2）在（1）所有组合中任选一组，并求对应的面积.（若所选条件出现多种可能，则按计算的第一种可能计分）20．(12分)如图，正方体的棱长为1，线段上有两个动点E，F，且.
    (1)若P为上的一点，则P到平面的距离．
    (2)求三棱锥的体积．
 21．(12分)已知函数，.（1）讨论的单调性；（2）若有两个极值点、，求的取值范围. (二)选考题：共10分。请考生在第22、23两题中任选一题做答，如果多做．则按所做的第一题记分。22．[选修4－4：坐标系与参数方程]在平面直角坐标系xOy中，射线l：(x≥0)，曲线C1的参数方程为（为参数），曲线C2的方程为；以原点为极点，x轴的非负半轴为极轴建立极坐标系，曲线C3的极坐标方程为．（1）写出射线l的极坐标方程以及曲线C1的普通方程；（2）已知射线l与C2交于O，M，与C3交于O，N，求的值．23．[选修4—5：不等式选讲]（10分）已知．
（1）求不等式的解集；（2）若的最小值为m，正实数a，b，c满足，求证：．
银川一中2021届高三第四次月考数学(文科)参考答案一、选择题：只有一项符合题目要求（共12小题，每小题5分，共60分）题号123456789101112答案CBADDCBAADCB11．【解析】连接、、，则为的中点，对于A选项，平面，平面，，、分别为、的中点，则，，A选项正确；对于B选项，四边形为正方形，则，又，，平面，，平面，B选项正确；对于C选项，易知为等边三角形，则，，则与所成的角为，C选项错误；对于D选项，，平面，平面，平面，D选项正确.12．【解析】解：在[，2]的值域为，但在（,2]递减,此时∈[﹣4，）．的导数为，可得在递减，递增，则在的最小值为，最大值为，即值域为[0，e]．对任意的，存在唯一的[，2]，使得可得，可得，解得．故选：B．二、填空题：（本大题共4小题，每小题5分，共20分）13．    14．或．    15．   16．16．【解析】设依次所作的第个正方形的边长为，第个正方形与第个等腰直角三角形的面积和为，则第个等腰直角三角形的腰长为，且.第个正方形的边长为，，，，且，所以，数列是以为首项，为公比的等比数列. 三、解答题：17．（1）；（2）2.【解析】（1）在等差数列中，设公差为d≠0，由题意，得，解得．∴an＝a1+（n﹣1）d＝1+2（n﹣1）＝2n﹣1；（2）由（1）知，an＝2n﹣1．则＝，∴Tn＝＝．18．证明：如图，取CD的中点E，连接NE，ME．，M，N分别是CD，AB，PC的中点，，，平面平面PDA，平面PAD．平面ABCD，．底面ABCD是矩形，，又，平面PAD，．，，又，，平面ENM，．，N是PC的中点，又，平面PCD．19.（1）①，③，④或②，③，④；（2）.【解析】（1）由①得，，所以，由②得，，解得或（舍），所以，因为，且，所以，所以，矛盾.所以不能同时满足①，②.故满足①，③，④或②，③，④；（2）若满足①，③，④，因为，所以，即.解得.所以的面积.若满足②，③，④由正弦定理，即，解得，所以，所以的面积.20．【解析】解：（1），平面，平面，
平面，即平面BEF，
又正方体的棱长为1，
到平面BEF的距离为到的距离，
若P为上的一点，则P到平面BEF的距离为，故正确；
（2），
设AC，BD交于点O，平面，，
，
21．（1）见解析；（2）.【解析】（1）函数的定义域为，，令.当，即时，，则对任意的恒成立，此时函数在上单调递增；当时，对任意的恒成立，此时函数在上单调递增；当时，有两个正根，分别为，，当或时，；当时，.此时函数在，上单调递增，在上单调递减.综上可得：当时，函数的单调递增区间是，无递减区间；当时，函数的单调递增区间是，，单调递减区间是；（2）由（1）可知、是关于的二次方程的两根，由韦达定理可得，，，，，，，，，令，则，设，，当时，，当时，.所以，函数在单调递增，在单调递减，，因此，的取值范围是.22．（1），（2）【解析】（1）依题意，因为射线，故射线消去方程中的参数可得，所以曲线的普通方程为：．（2）曲线的方程为，即，把代入上式可得曲线的极坐标方程为，设点对应的极径分别为，则． 23.【答案】解：
当时，由，得，此时无解；
当时，由，得，此时的解为；
当时，由，解得，此时的解为．
综上，不等式的解集为；
证明：，
故的最小值为，．

，
等号当且仅当，即时成立．
，，
，
即．