

高三数学 数列专题复习 二十六 等比数列考点汇编
展开专题二十六 等比数列
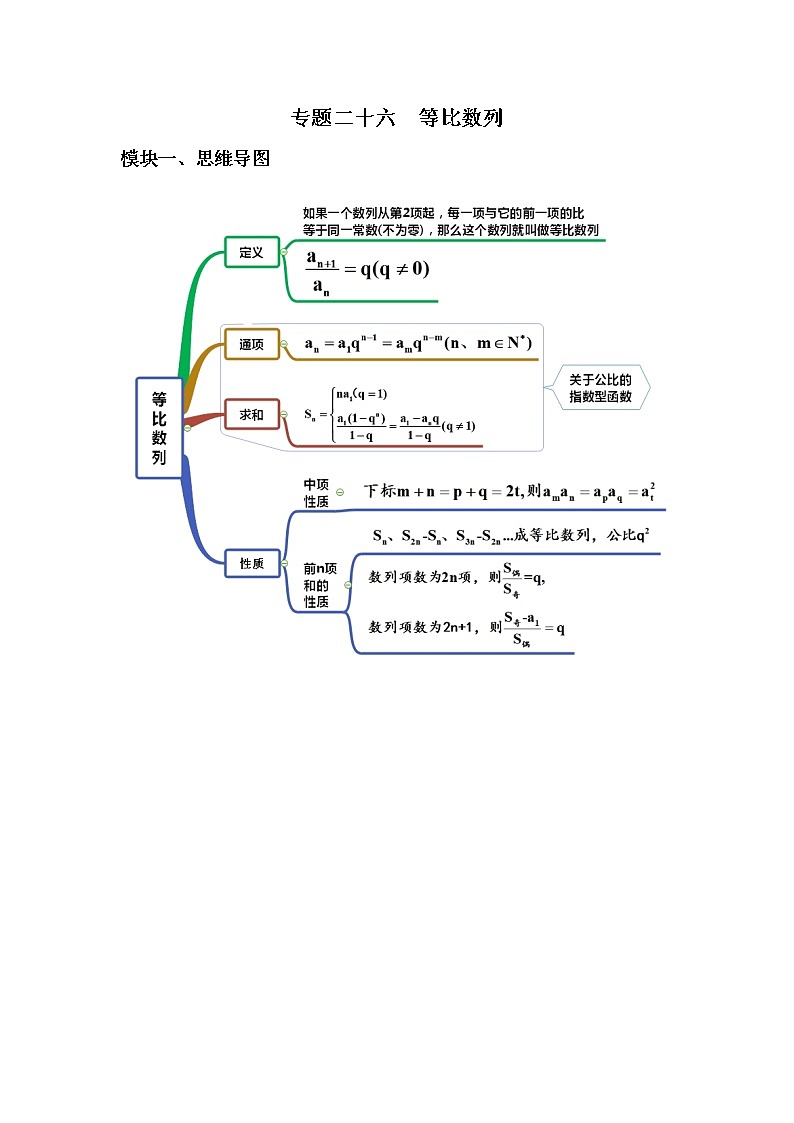
模块一、思维导图
模块二、考法梳理
考法一:定义的运用
1.已知数列,,,.求证:是等比数列;
【解析】依题意,,
所以,是首项为2、公比为2的等比数列.
2.已知数列的前项和为,且,.求证:为等比数列,并求的通项公式;
【解析】由得:,两式相减得:
,即,∴,
由,令得,而,故,
所以为首项是2,公比是2的等比数列,故,.
3.已知数列中,其前项和满足.求证:数列为等比数列,并求的通项公式;
【解析】当时,,可得;
当时,,即有,
则数列为首项为2,公比为2的等比数列,可得,
考法二:中项性质
1.已知实数依次成等比数列,则实数的值为 。
【解析】因为实数依次成等比数列,所以有
当时,,显然不存在这样的实数,故
2.已知数列是等比数列,函数的两个零点是,则 。
【答案】
【解析】由韦达定理可知,,则,,从而,且,
3.在等比数列中,,是方程的两根,则
【答案】
【解析】在等比数列中,由题意知:,,
所以,,所以,即.
4.在正项等比数列中,,则_______
【答案】
【解析】由正项等比数列的的性质以及等比中项公式可得:
,
则:
.故答案为:-2019.
5.己知数列为正项等比数列,且,则
【答案】2
【解析】∵数列为等比数列,且∴,
即,又,∴.
6.实数数列为等比数列,则 。
【解析】由题意,,又与同号,∴.
7.在等比数列中,,是方程的两个根,则的值为 。
【答案】或
【解析】等比数列中,,是方程的两个根
8.已知,若2是与等比中项,则的最小值为 。
【解析】∵2是与的等比中项,
∴,∴,即,
结合可得,,
∴
,
当且仅当,即,时取等号,
即的最小值为,
9.已知四个实数成等差数列,五个实数成等比数列,则 。
【解析】先由等差数列和等比数列的性质,得,;再利用等比数列中的第三项和第一项同号,得;所以
10.在中,角A,B,C对应的边分别为a,b,c,若a,b,c成等比数列且,则 。
【答案】
【解析】由a,b,c成等比数列,可得,则,
又,利用正弦定理可得,,则,
故,所以,
所以.
11.若△ABC的内角A、B、C所对的边a、b、c成等比数列,则的取值范围是 。
【答案】
【解析】
可得:
即
由,所以
因为a、b、c成等比数列,所以即,令
又,则化简可得:即,所以
考法三:前n项和的性质
1.已知等比数列的前n项和为,且,,则 。
【答案】19
【解析】因为等比数列的前n项和为,所以,,成等比数列,因为,,所以,,故.
2.已知等比数列的前项和为,,,则 。
【答案】4
【解析】因为成等比数列,所以
代入数值所以,则.
3.设等比数列的前项和记为,若,则 。
【答案】
【解析】∵数列为等比数列,且其前项和记为,∴成等比数列.
∵,即,∴等比数列的公比为,
∴,∴,∴.
4.若等比数列的前项和为,已知,,则 。
【答案】7
【解析】依题意,显然数列的公比,所以,,也成等比数列,
且公比为,所以,所以,所以,
5.各项均为正数的等比数列的前项和,若,,则的最小值为。
【答案】8
【解析】因为,且等比数列各项均为正数,所以
公比首项 所以 ,通项
所以 当且仅当
所以当时,的最小值为8
6.设正项等比数列的首项,前项和为,且,则公比的值为 。
【答案】
【解析】化简得
因为为等比数列,为其前项和,所以所以
7.已知一个等比数列首项为1,项数是偶数,其奇数项之和为341,偶数项之和为682,则这个数列的项数为 。
【答案】10
【解析】设等比数列项数为2n项,所有奇数项之和为S奇,所有偶数项之和为S偶,
则S奇=341,S偶=682,所以 ,∴ ,解得n=5,
这个等比数列的项数为10,
8.已知正项等比数列的前项和为,且,则的最小值为 。
【解析】因为是等比数列,所以,且也是等比数列,所以
整理有 (当且仅当时取等号)
所以的最小值为
考法四:实际运用
1.我国古代学者庄子在《庄子·天下篇》中提到:“一尺之棰,日取其半,万世不竭”,指一尺长的木棒,今天取其一半,明天取剩下的一半,后天再取剩下的一半,永远也取不尽.现有尺长的线段,每天取走它的,天后剩下的线段长度不超过尺,则的最小值为 。
【解析】由题意可知:第一天取走,剩下尺,第二天剩下尺,第三天剩下尺, 第九天剩下尺,第十天剩下尺,答案:10
2.中国古代数学著作《算法统宗》中记载了这样的一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还”,其大意为:有一个人走了378里路,第一天健步行走,从第二天起其因脚痛每天走的路程为前一天的一半,走了6天后到达了目的地,问此人第三天走的路程里数为 。
【解析】由题意可知此人行走的里程数为等比数列
设第一天行走的路程为,且等比数列的公比为
则由等比数列的前n项和公式代入可得
解得 根据等比数列的通项公式代入可得
3.“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分为十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于.若第一个单音的频率,则第八个单音频率为 。
【解析】设从第一单音起,每个单音的频率记为,从第二个单音起,
每一个单音的频率与它的前一个单音的频率的比都等于,
第一个单音的频率,所以是以为首项,
公比为的等比数列,.【答案】
4.中国古代数学名著《九章算术》中有这样一个问題:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马、“马主曰:“我马食半牛,”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟、羊主人说:“我羊所吃的禾苗只有马的一半,”马主人说:“我马所吃的禾苗只有牛的一半,“打算按此比例偿还,他们各应偿还多少?该问题中,1斗为10升,则马主人应偿还 升粟。
【解析】因为斗=升,设羊、马、牛的主人应偿还的量分别为,
由题意可知其构成了公比为2的等比数列,且
则,解得,所以马主人要偿还的量为:,【答案】
5.中国古代数学著作《算法统宗》中有这样一个问题:“一百八十九里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行数里,请公仔细算相还”,其意思为:“有一个人要走189里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,请问第二天走了 。
【解析】记第天行走的路程为,则数列为等比数列,公比,
依题意知,前项的和,即,所以,解得,
所以,所以第二天行走了48里.
6.某个蜂巢里有一只蜜蜂,第一天它飞出去带回了五个伙伴,第二天六只蜜蜂飞出去各自带回五个伙伴,如果这个过程继续下去,那么第六天所有的蜜蜂归巢后蜂巢中共有蜜蜂的数量是 。
【答案】只
【解析】设第天所有的蜜蜂归巢后蜂巢中共有蜜蜂只,
由题意可得:,即,所以数列为等比数列即
所以第六天所有的蜜蜂归巢后蜂巢中共有蜜蜂的数量是
模块三、巩固提升
【考法一 定义的运用】
1.已知数列满足(,),且,.证明:数列是等比数列;
【答案】见解析
【解析】证明:∵当时,,∴. ∴,.
∴数列是以2为首项,公比为2的等比数列.
2.在数列中,,,且对任意的N*,都有.证明数列是等比数列,并求数列的通项公式;
【答案】见证明;
【解析】由可得.
又,,所以,故.
所以是首项为2,公比为2的等比数列.所以.
所以.
3.已知数列满足若数列满足,求证:是等比数列;
【答案】见解析.
【解析】由题可知,从而有,,所以是以1为首项,3为公比的等比数列.
4.已知数列中,,,.设.证明:数列是等比数列;
【答案】证明见解析;
【解析】证明:因为,,
所以 ,
又因为, 所以数列是以1为首项,以2为公比的等比数列.
5.设数列的前项和为,且.证明:是等比数列,并求其通项公式;
【答案】(1);(2).
【解析】当时,,所以,
当时,,,两式相减得,所以.
因此是首项为,公比为的等比数列.于是.
6.已知数列满足,设.证明数列为等比数列;
【答案】证明见详解;
【解析】(1)证明:由可得.
而,所以.又,所以数列为等比数列.
【考法二 中项性质】
1.正项等比数列中,,且与的等差中项为4,则的公比是 。
【解析】由题意,正项等比数列中,,
可得,即,与的等差中项为4,即,
设公比为q,则,则负的舍去,
2.设是首项为,公差为-1的等差数列,为其前n项和,若成等比数列,则= 。
【解析】因为成等比数列,所以,即
3.如果-1,a,b,c,-9成等比数列,那么b= ,ac= 。
【解析】因为
4.设,,若是与的等比中项,则的最小值为 。
【解析】由题意可得,即,得,所以,,
,,由基本不等式得,
当且仅当时,即当时,等号成立,因此,的最小值为.
5.正项等比数列(),若存在, 使得,则最小值为 。
【解析】∵正项等比数列{an}满足:,又q>0,解得,∵存在两项am,an使得,∴,即,
∴,
当且仅当=取等号,但此时m,n∉N*.又,所以只有当,取得最小值是.
6.已知各项均为正数的等比数列{},=5,=10,则= 。
【解析】由等比数列的性质知,a1a2a3,a4a5a6,a7a8a9成等比数列,所以a4a5a6=
故答案为
7.已知数列是首项,公比的等比数列,且,,成等差数列则公比等于 。
【解析】数列是首项,公比的等比数列,且,,成等差数列,,,解得(舍或.
8.的内角的对边分别为,若既是等差数列又是等比数列,则角的值为 。
【【解析】由题意得:,
由余弦定理得:
9.若等比数列中,且,则与的等比中项等于______.
【解析】且
,设与的等比中项为,则故与的等比中项为
10.已知实数列成等比数列,则等于 。
【解析】根据等比数列的通项公式,可知由等比中项定义可知
所以 所以
11.在中,角的对边分别为,若为等比数列,且,则______.
【答案】
【解析】由是等比数列,则,,
由余弦定理可得,,即,
解得或,
因为,
因为,所以,
当时,由正弦定理可得,所以,,则;
当时,同理可得,,所以,
故答案为:
【考法三---前n项和的性质】
1.若等比数列的前项和为,已知,,则 。
【答案】7
【解析】依题意,显然数列的公比,所以,,也成等比数列,
且公比为,所以,所以,所以
2.设等比数列中,前n项和为,已知,则等于 。
【解析】因为,且也成等比数列,.
即8,-1,成等比数列,所以,即所以
3.等比数列的前项和为,若,,则 。
【解析】由题有等比数列的前项和满足成等比数列.设的公比为则,故.
故,即.
因为故.又
故,故.
4.等比数列的前项和为,公比为,若,,则 。
【解析】由题意得∵,,∴,根据等比数列的性质可知,,,构成等比数列,故,∴,
故.
5.各项均为正数的等比数列的前项和为,已知,,则_________.
【解析】在等比数列中, ,,也成等比数列,
即成等比数列, 解得
故答案为:
6.在等比数列中,,,则的值是 .
【答案】8
【解析】设等比数列的公比为,因为,即,,
则,又由.
7.等比数列的首项为,公比为,前项和为,则当时,的最大值与最小值的比值为 .
【解析】∵等比数列的首项为,公比为∴∴.
①当为奇数时,随着的增大而减小,则,故;
②当为偶数时,随着的增大而增大,则,故.
∴的最大值与最小值的比值为
8.已知等比数列的前n项和为,,,且,则满足不等式成立的最小正整数n为________.
【答案】
【解析】设数列的公比为q,由,,得,所以或,
又因为,所以,从而,所以.
令,又因为,所以.故答案为:6
9.已知为正项等比数列的前n项和,若,则的最小值为________.
【答案】
【解析】由等比数列的性质,,,成等比数列,且
故,当且仅当时,等号成立,所以最小值为32.故答案为:32
【考法四 实际运用】
1.《九章算术》中有一题:今有牛、马羊食人苗,苗主贵之粟五斗,羊主日:“我羊食半马,”马主曰:“我马食半牛”,今欲衰偿之,问各出几何?其意:今有牛、马、羊吃了别人的禾苗,苗主人要求赔偿五斗粟,羊主人说: “我羊所吃的禾苗只有马的一半”,马主人说:“我马所吃的禾苗只有牛的一半”,打算按此比例偿还,则牛主人比羊主人多赔偿 斗粟
【答案】
【解析】由题意,羊马牛的主人需赔偿的粟,依次成等比数列,且公比,
因为一共赔偿五斗粟,所以,即,即,
所以,因此,所以.即牛主人比羊主人多赔偿斗粟.
2.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人要走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”则该人第四天走的路程为 .
【答案】24里
【解析】该人从第一天起每天走得路程记为,则是公比为的等比数列,
,解得,.
3.十二平均律是我国明代音乐理论家和数学家朱载填发明的.明万历十二年(公元1584年),他写成《律学新说》,提出了十二平均律的理论,这一成果被意大利传教士利玛窦通过丝绸之路带到了西方,对西方音乐产生了深远的影响.十二平均律的数学意义是:在1和2之间插入11个正数,使包含1和2的这13个数依次成递增的等比数列.依此规则,插入的第四个数应为 .
【答案】
【解析】由题意设这13个数依次成递增的等比数列为,满足
4.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走了378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”问此人第5天和第6天共走了 .
【答案】18里
【解析】设第1天走了里,每天所走的路程为, 依题意成公比为,前6项和为378
,解得,.
5.我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯 .
【答案】3盏
【解析】设塔的顶层共有灯a盏,则各层的灯数从上到下构成一个以2为公比的等比数列,
由 得








