




初中人教版12.2 三角形全等的判定优质课ppt课件
展开
这是一份初中人教版12.2 三角形全等的判定优质课ppt课件,共20页。PPT课件主要包含了边边边SSS,角边角ASA,角角边AAS,边角边SAS,ASA,AAS,SAS,SSS,⑷连接A'B',跟踪训练等内容,欢迎下载使用。
1.经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;2.掌握直角三角形全等的条件,并能运用其解决一些实际问题;3.在探索直角三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理.
我们已经学过判定全等三角形的方法有哪些?
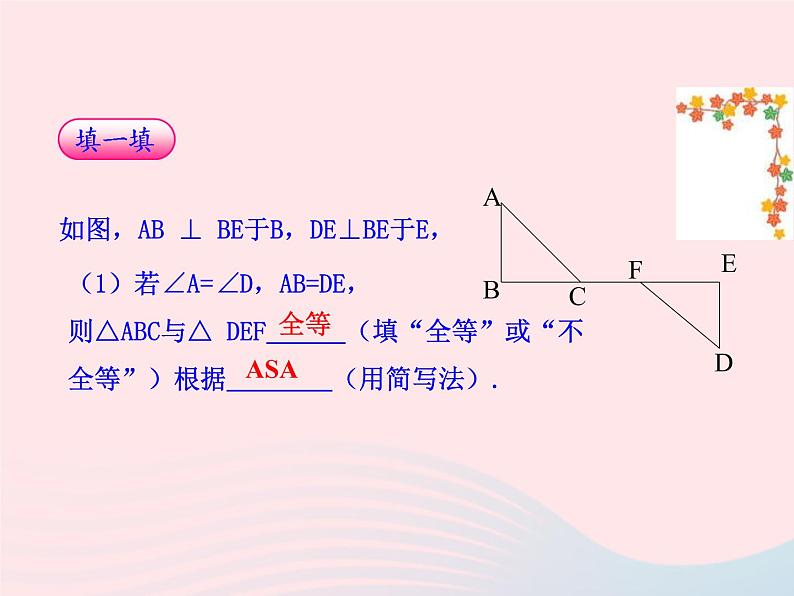
如图,AB ⊥ BE于B,DE⊥BE于E,
(1)若 A= D,AB=DE,则△ABC与△ DEF (填“全等”或“不全等”)根据 (用简写法).
(2)若 A= D,BC=EF,则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法).
(3)若AB=DE,BC=EF,则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法).
(4)若AB=DE,BC=EF,AC=DF,则 △ABC与△DEF (填“全等”或“不全等”)根据_____(用简写法).
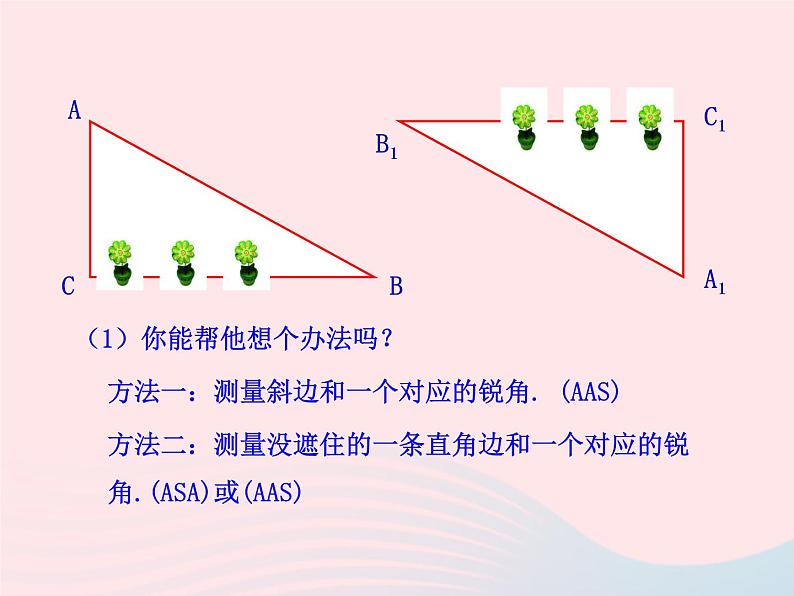
如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
(1)你能帮他想个办法吗?
方法一:测量斜边和一个对应的锐角. (AAS)
方法二:测量没遮住的一条直角边和一个对应的锐 角.(ASA)或(AAS)
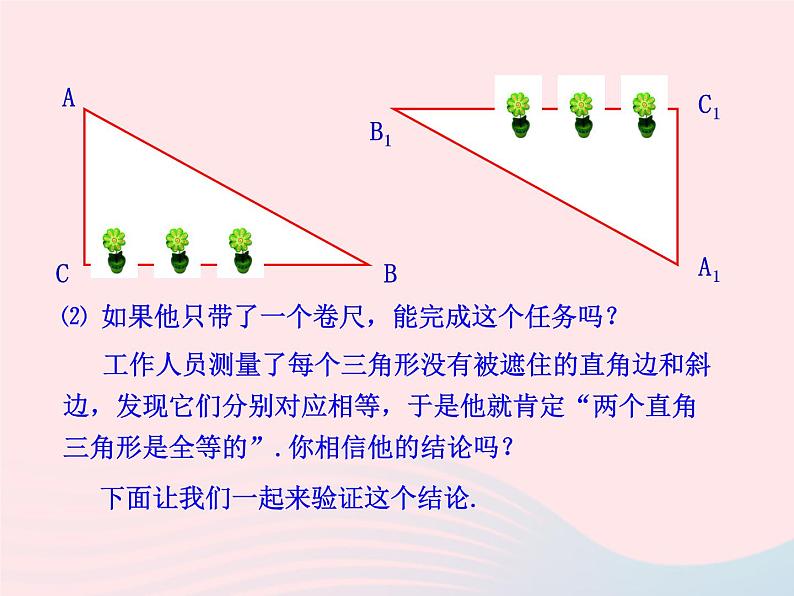
⑵ 如果他只带了一个卷尺,能完成这个任务吗?
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗?
下面让我们一起来验证这个结论.
任意画一个Rt△ACB ,使∠C﹦90°,再画一个Rt△A′C′B′使∠C′=∠C ,B′C′﹦BC,A′B′﹦AB,(1)你能试着画出来吗?与小组交流一下.(2)把画好的Rt△A′C′B′放到Rt△ACB上,它们全等吗?你能发现什么规律?
⑴ 作∠MC'N=90°;
⑵ 在射线C'M上截取线段 C'B'=CB;
⑶ 以B'为圆心,BA为半径画弧,交射线C'N于点A';
斜边和一条直角边分别相等的两个直角三角形全等.简写成“斜边、直角边”或“HL”.
【例】如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
【解析】在Rt△ABC和Rt△DEF中,
∴ Rt△ABC≌Rt△DEF (HL).
∴∠ABC=∠DEF(全等三角形对应角相等).
∵ ∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
1.如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证:BC=AD.
【证明】∵AC⊥BC, BD⊥AD,∴∠C 与∠D都是直角.在Rt△ABC和Rt△BAD中,又∵AB=BA AC=BD,∴Rt△ABC≌Rt△BAD(HL),∴BC=AD.
1.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE.
【证明】在Rt△ABF和Rt△CDE中,∵AE=CF,∴AF=CE.又∵AB=CD,∴Rt△ABF≌Rt△CDE(HL),∴BF=DE.
2. 如图,两根长度为12 m的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.
BD=CD.∵∠ADB=∠ADC=90°, AB=AC AD=AD
∴Rt△ABD≌Rt△ACD(HL),∴ BD=CD.
1.(温州·中考)如图,AC,BD是矩形ABCD的对角线,过点D作DE∥AC交BC的延长线于E,则图中与△ABC全等的三角形共有( )A.1个 B.2个 C.3个 D.4个
【解析】选D.在矩形ABCD中,△CDA、△BAD、△DCB都和△ABC全等,又∠ABC=∠DCE=90°,DE∥AC,所以∠DEC=∠ACB;又AB=DC,所以△DCE也和△ABC全等.
2. 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
在Rt△ACB和Rt△ADB中,
∴ Rt△ACB≌Rt△ADB (HL).
∴BC=BD(全等三角形对应边相等).
相关课件
这是一份人教版八年级上册12.2 三角形全等的判定习题课件ppt,共34页。
这是一份数学八年级上册第十二章 全等三角形12.2 三角形全等的判定说课ppt课件,共29页。PPT课件主要包含了SSS,SAS,ASA,AAS,动脑想一想等内容,欢迎下载使用。
这是一份初中数学人教版八年级上册第十二章 全等三角形12.2 三角形全等的判定优质ppt课件,共8页。









