人教版18.2.1 矩形教学演示课件ppt

这是一份人教版18.2.1 矩形教学演示课件ppt，共9页。PPT课件主要包含了矩形的判定，∴∠BAD∠CDA，∵AB∥CD，猜想加证明，动手探究，随堂练等内容，欢迎下载使用。

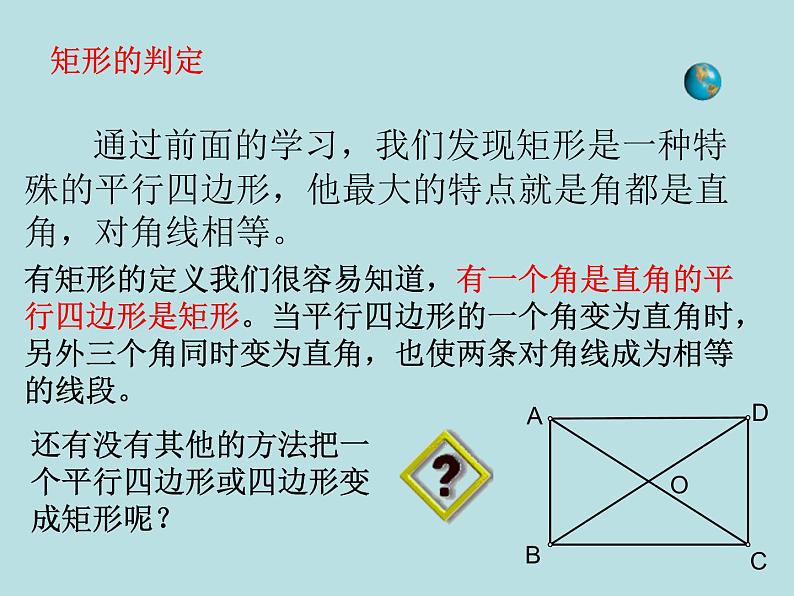
通过前面的学习，我们发现矩形是一种特殊的平行四边形，他最大的特点就是角都是直角，对角线相等。
有矩形的定义我们很容易知道，有一个角是直角的平行四边形是矩形。当平行四边形的一个角变为直角时，另外三个角同时变为直角，也使两条对角线成为相等的线段。
还有没有其他的方法把一个平行四边形或四边形变成矩形呢？
结论：对角线相等的平行四边形是矩形
AB=DC,BD=CA,AD=DA
∴△BAD≌△CDA(SSS)
∴∠BAD +∠CDA=180°
∴∠BAD＝90°
∴四边形ABCD是矩形（有一个内角是 直角的平行四边形是矩形）
对角线相等的平行四边形是矩形吗？
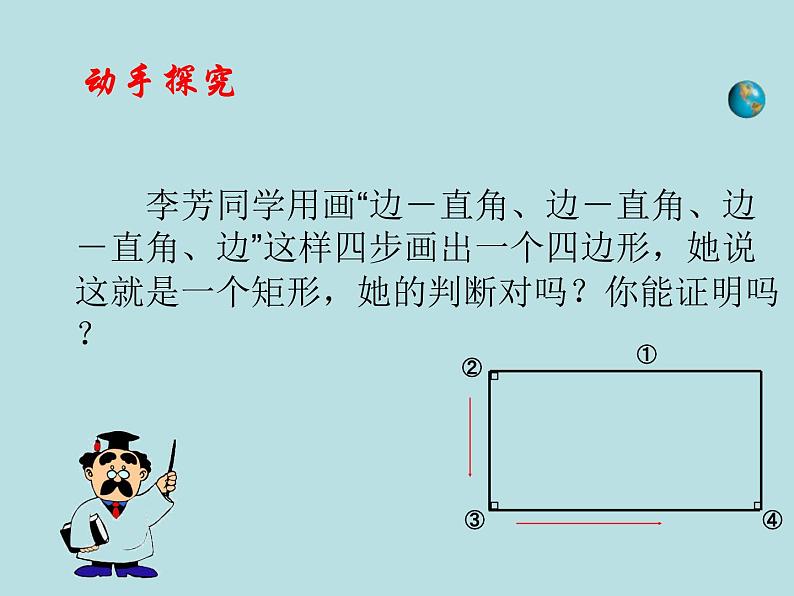
　　李芳同学用画“边－直角、边－直角、边－直角、边”这样四步画出一个四边形，她说这就是一个矩形，她的判断对吗？你能证明吗？
定理:有三个角是直角的四边形是矩形.
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
分析:利用同旁内角互补,两直线平行来证明四边形是平行四边形,可使问题得证.
∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形.
　　　1、能够判断一个四边形是矩形的条件是（ ）　　　　A 对角线相等 B 对角线垂直　　　　C对角线互相平分且相等 D对角线垂直且相等 2、矩形的一组邻边长分别是3cm和4cm，则它的对角线长是 cm3、如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线，则四边形ABCD是（ ） A 菱形 B 平行四边形 C 矩形 D 不能确定
　　1、如图，矩形ABCD的对角线AC、BD相交于O，∠BOC=2 ∠ AOB，若AC=6cm,试求AB的长.2、如图，O是菱形ABCD对角线的交点，作DE∥AC，CE∥BD，DE、CE交于点E，四边形CEDO是矩形吗？说出你的理由.
已知:如图,四边形ABCD是平行四边形,P是CD上的一点,且AP和BP分别分别平分∠DAB和∠CBA,QP∥AD,交AB于点Q.(1).求证:AP⊥PB;(2).如果AD=5cm,AP=8cm,那么AB的长是多少? △APB的面积是多少?