


人教版八年级下册18.1.1 平行四边形的性质获奖课件ppt
展开
这是一份人教版八年级下册18.1.1 平行四边形的性质获奖课件ppt,共10页。
2.两条平行线之间的距离两条平行线中,一条直线上的任意一点到另一条直线的 ,叫做这两条平行线之间的距离. 3.平行四边形的面积平行四边形的面积等于 乘以 .
探究点一:两条平行线之间的距离
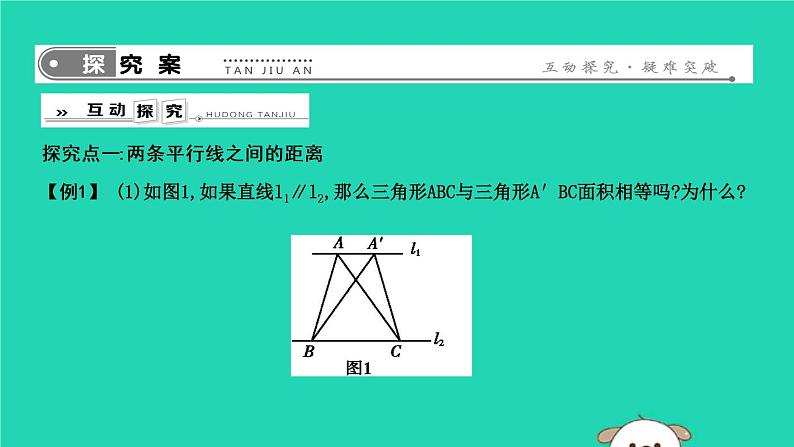
【例1】 (1)如图1,如果直线l1∥l2,那么三角形ABC与三角形A′BC面积相等吗?为什么?
【导学探究】 1.△ABC和△A′BC的底边都为 ,由平行线间的距离处处相等,可知△ABC和△A′BC的BC边上的 相等.
解:(1)相等.因为l1∥l2,所以l1,l2之间的距离是固定的,所以△ABC和△A′BC的BC边上的高相等,所以△ABC和△A′BC的面积相等.
(2)如图2,平行四边形ABCD与平行四边形AB′C′D有一条公共边AD,BC和B′C′在同一直线上,这两个平行四边形的面积相等吗?为什么?【导学探究】 2.由平行线间的距离处处相等,所以平行四边形ABCD与平行四边形AB′C′D的 相等.
解:(2)相等.因为四边形ABCD为平行四边形,所以AD∥BC,所以AD和BC之间的距离是固定的,因为BC和B′C′在同一直线上,所以平行四边形ABCD与平行四边形AB′C′D公共边AD边上的高相等,所以平行四边形ABCD与平行四边形AB′C′D面积相等.
等底(或同底)等高(或同高)的两个平行四边形的面积相等.
【例2】已知:如图,在▱ABCD中,对角线AC,BD交于点O,AB⊥AC,AB=1,BC= .(1)求对角线BD的长;【导学探究】1.由▱ABCD的性质可得,AO= ,BO= .
探究点二:平行四边形对角线性质
(2)求平行四边形ABCD的面积S▱ABCD.【导学探究】2.平行四边形的面积= ×高.
解:(2)S▱ABCD=AB·AC=1×2=2.
(1)平行四边形中,对角线互相平分是计算或证明常用的结论.(2)当平行四边形中有一条对角线时,常作出另一条对角线,利用对角线的性质.
1.平行四边形具有的特征是( )(A)四个角都是直角(B)对角线相等(C)对角线互相平分(D)四边相等2.(2018宜兴期中)已知点O是▱ABCD对角线的交点,△ABC的面积是3,则▱ABCD的面积是( )(A)3(B)6(C)9(D)123.(2018新罗月考)已知一个平行四边形,两邻边长分别为6和8,两长边的距离为3,则两短边之间的距离为 .
相关课件
这是一份初中数学湘教版八年级下册2.2.1平行四边形的性质多媒体教学课件ppt,共13页。PPT课件主要包含了新课导入,如何证明,随堂练习等内容,欢迎下载使用。
这是一份人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.1 平行四边形的性质优秀课件ppt,共8页。PPT课件主要包含了平行且相等,ADE等内容,欢迎下载使用。
这是一份初中数学人教版八年级下册18.1.1 平行四边形的性质优质习题课件ppt,










