苏科版3.1 勾股定理评优课ppt课件

这是一份苏科版3.1 勾股定理评优课ppt课件，共17页。PPT课件主要包含了探究1，SA+SBSC，a2+b2c2，用拼图法证明，方法小结，试一试，拓展练习等内容，欢迎下载使用。
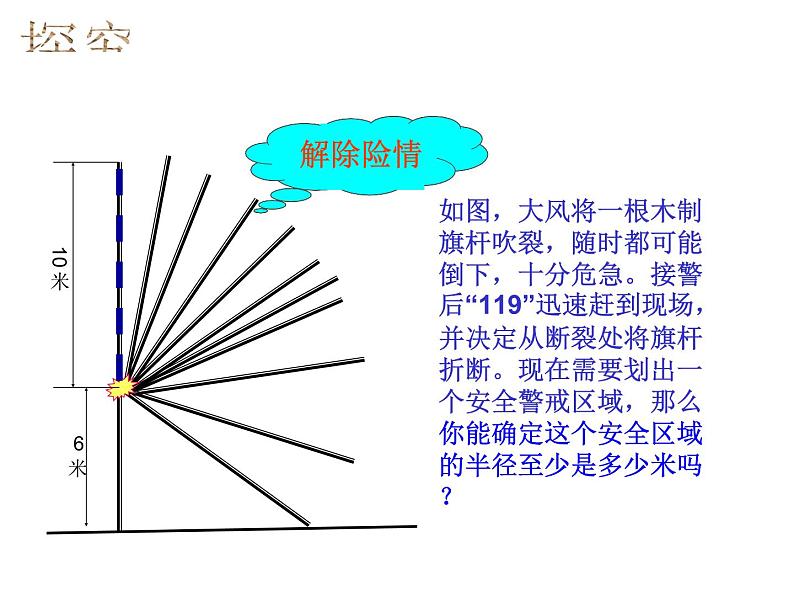
如图，大风将一根木制旗杆吹裂，随时都可能倒下，十分危急。接警后“119”迅速赶到现场，并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域，那么你能确定这个安全区域的半径至少是多少米吗？
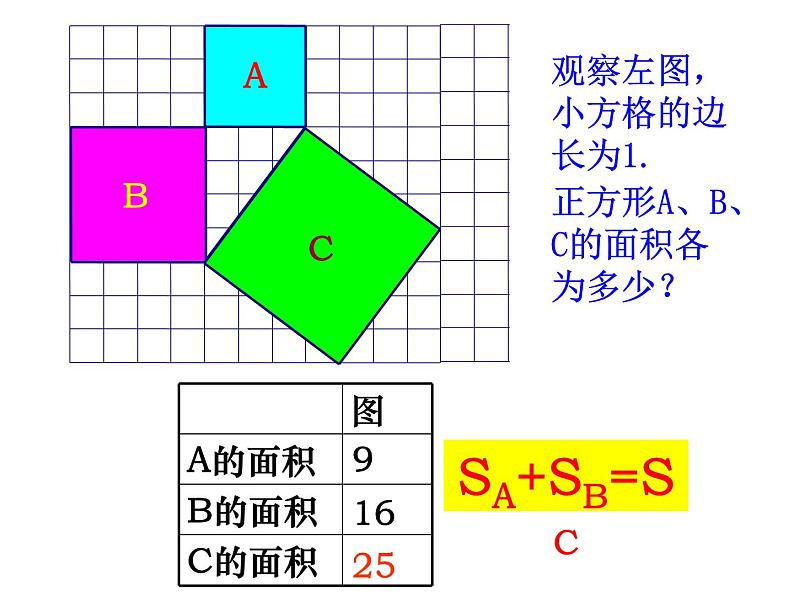
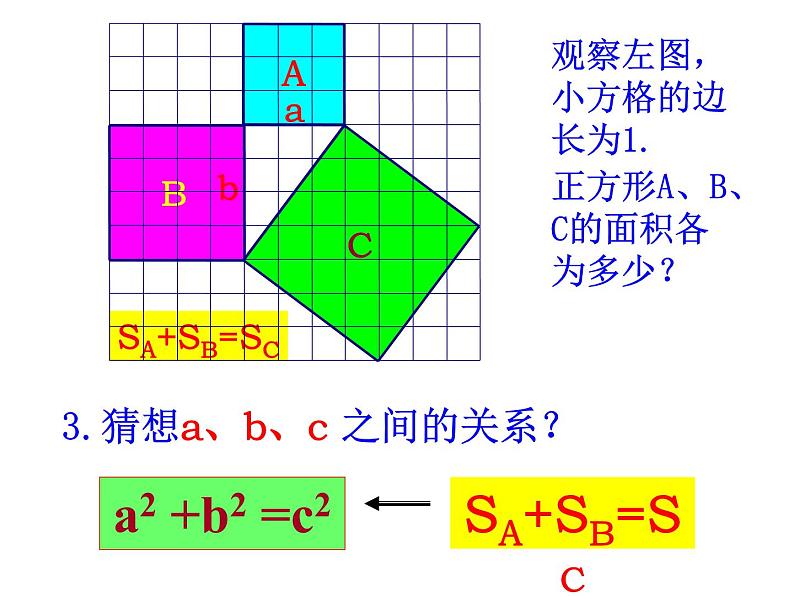
观察左图，小方格的边长为1.正方形A、B、C的面积各为多少？
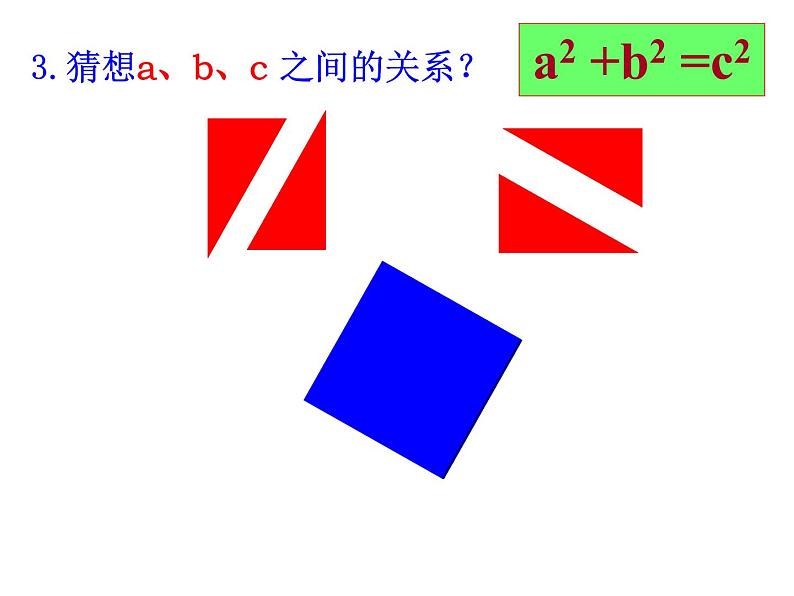
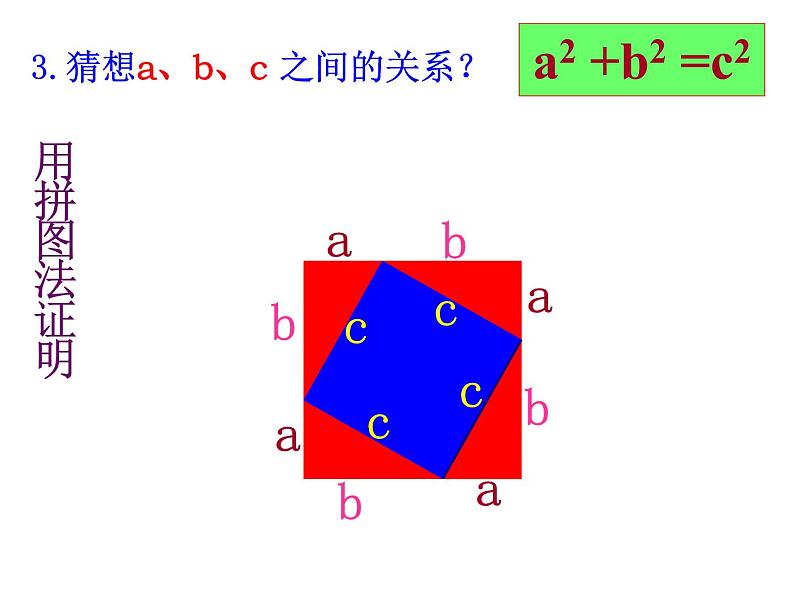
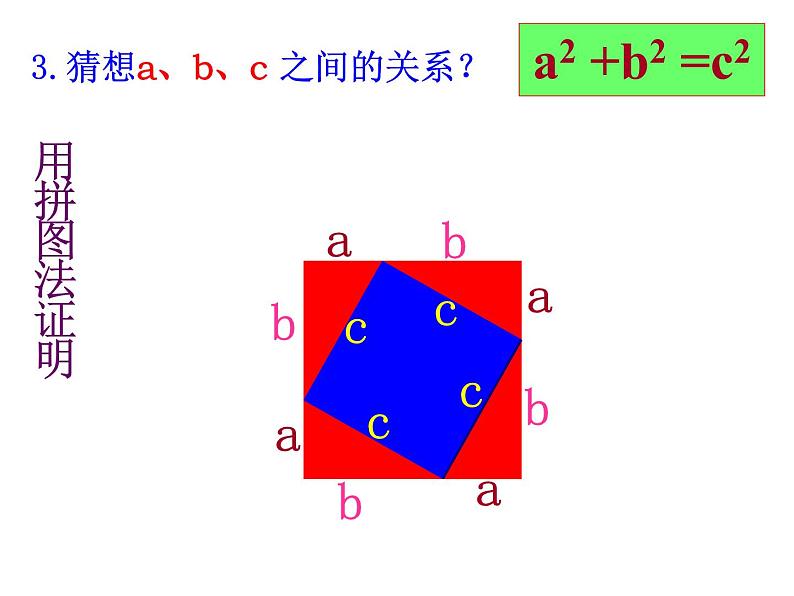
3.猜想a、b、c 之间的关系？
∵S大正方形=(a+b)2=a2+b2+2ab S大正方形=4S直角三角形+ S小正方形 =4x ab+c2 =c2+2ab
∴a2+b2+2ab=c2+2ab
∴a2 +b2 =c2
勾股定理(毕达哥拉斯定理) （gu－gu therem）
如果直角三角形两直角边分别为a， b，斜边为c，那么
勾股定理的条件是什么？ 结论是什么？
勾股定理是否对所有的三角形都适用？勾股定理有怎样的用途？
用途：勾股定理揭示了在直角三角形中已 知任意二边可以求第三边。
如图，在△ABC中，∠C＝90°： 若a=15,b=8，则c= ;若a=4,c=5，则b= ;若b=5,c=13,则a=
(1)在直角三角形中,已知两边,可求第三边;(2)可用勾股定理建立方程.
４、已知：Rt△ＡBC中，AB＝４，AC＝３,则BC的长为 .
如图,在Rt△AOB中，∠AO=90°, AO=6米 ,AB=10米, 由勾股定理，得 所以，这个安全区域的半径至少是8米
分析：木杆断裂后，AC那段到达AB位置，因此，AB=AC
1、在等腰△ABC中，AB＝AC＝13cm ，BC=10cm,求△ABC的面积和AC边上的高。
提示：利用面积相等的关系
2、 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm,则正方形A，B，C，D的面积之和为___________cm2。