苏科版八年级上册第三章 勾股定理3.3 勾股定理的简单应用完美版ppt课件

这是一份苏科版八年级上册第三章 勾股定理3.3 勾股定理的简单应用完美版ppt课件，共14页。PPT课件主要包含了解如图，议一议，练一练，试一试等内容，欢迎下载使用。

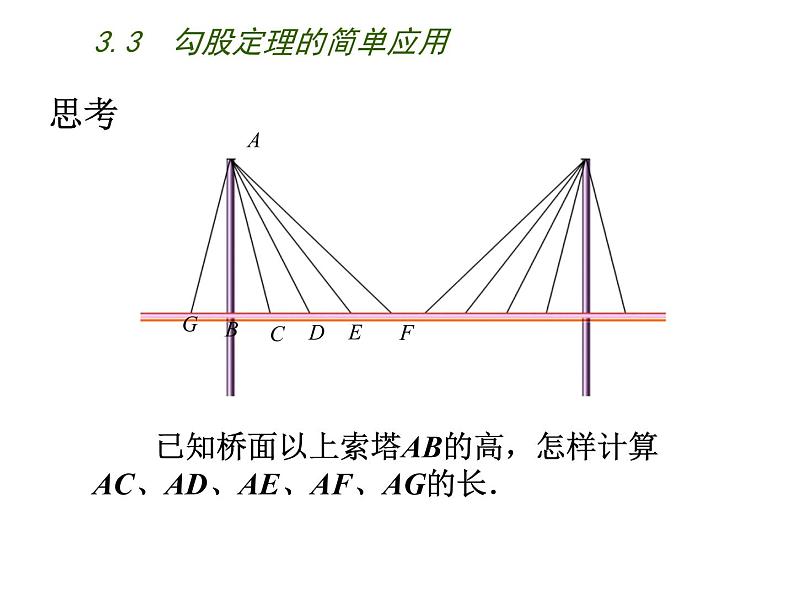
　　从远处看，斜拉桥的索塔、桥面与拉索组成许多直角三角形．
3.3　勾股定理的简单应用
　　已知桥面以上索塔AB的高，怎样计算AC、AD、AE、AF、AG的长．
例1　九章算术中的“折竹”问题：今有竹高一丈，末折抵地，去根三尺，问折者高几何？
　　意思是：有一根竹子原高1丈（1丈＝10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？
解：如图，我们用线段OA和线段AB来表示竹子，其中线段AB表示竹子折断部分，用线段OB来表示竹梢触地处离竹根的距离．设OA＝x，则AB＝10－x．
∵∠AOB＝90°，∴OA2＋OB2＝AB2，∴x2＋32＝（10－x）2．
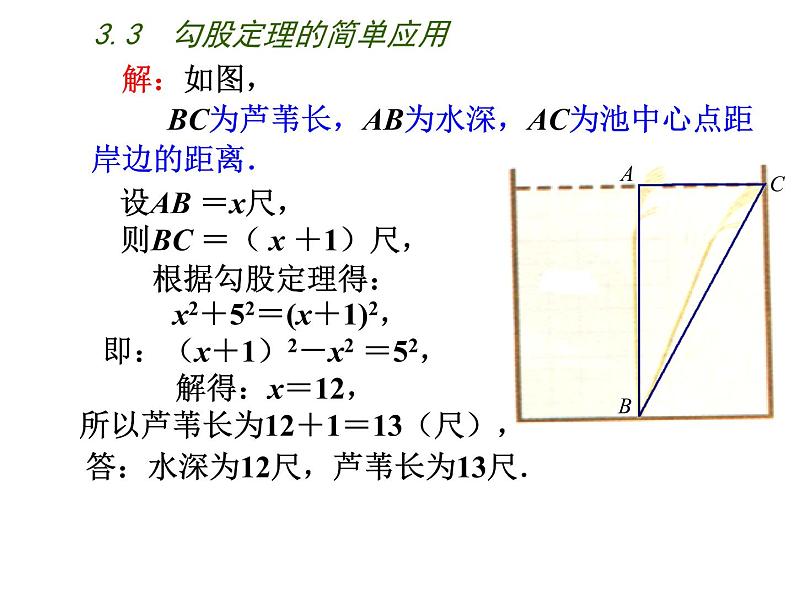
　“引葭赴岸”是《九章算术》中另一道题“今有池方一丈，葭生其中央，出水一尺,引葭赴岸，适与岸齐．问水深、葭长各几何？”
　　题意是：有一个边长为10尺的正方形池塘，在水池正中央有一根新生的芦苇，它高出水面1尺，如果把这根芦苇沿与水池边垂直的方向拉向岸边，它的顶端恰好到达岸边．请问这个水池的深度和这根芦苇的长度各是多少？
　　BC为芦苇长，AB为水深，AC为池中心点距岸边的距离．
　　　　　设AB ＝x尺，则BC ＝（ x ＋1）尺，根据勾股定理得： x2＋52＝(x＋1)2，即：（x＋1）2－x2 ＝52，解得：x＝12， 所以芦苇长为12＋1＝13（尺）， 　答：水深为12尺，芦苇长为13尺． 
例2　如图，在△ABC中， AB＝26，BC＝20，BC边上的 中线AD＝24，求AC.
∴BD＝CD＝ BC＝ ×20＝10．∵AD2＋BD2＝576＋100＝676， AB 2＝262＝676，
勾股定理与它的逆定理在应用上有什么区别？
　勾股定理主要应用于求线段的长度、图形的周长、面积； 　勾股定理的逆定理用于判断三角形的形状．
1．如图，在△ABC中， AB＝AC＝17，BC＝16，求△ABC的面积．
2．如图，在△ABC中，AD⊥BC，AB＝15，AD＝12，AC＝13，求△ABC的周长和面积．
如图，以△ABC的三边为直径向外作半圆，且S1＋S3＝S2，试判断△ABC的形状？
　　从勾股定理的应用中我们进一步体会到直角三角形与等腰三角形有着密切的联系；把研究等腰三角形转化为研究直角三角形，这是研究问题的一种策略．