苏科版八年级上册第三章 勾股定理3.3 勾股定理的简单应用优秀课件ppt

这是一份苏科版八年级上册第三章 勾股定理3.3 勾股定理的简单应用优秀课件ppt，共13页。PPT课件主要包含了议一议，练一练等内容，欢迎下载使用。

把勾股定理送到外星球，与外星人进行数学交流 ！ ——华罗庚
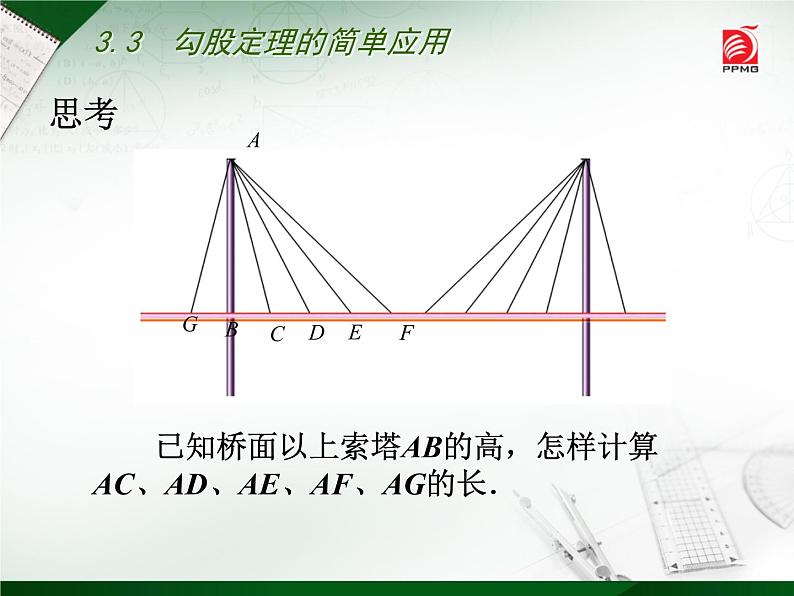
　　从远处看，斜拉桥的索塔、桥面与拉索组成许多直角三角形．
3.3　勾股定理的简单应用
　　已知桥面以上索塔AB的高，怎样计算AC、AD、AE、AF、AG的长．
例1　九章算术中的“折竹”问题：今有竹高一丈，末折抵地，去根三尺，问折者高几何？
　　意思是：有一根竹子原高1丈（1丈＝10尺），中部有一处折断，竹梢触地面处离竹根3尺，试问折断处离地面多高？
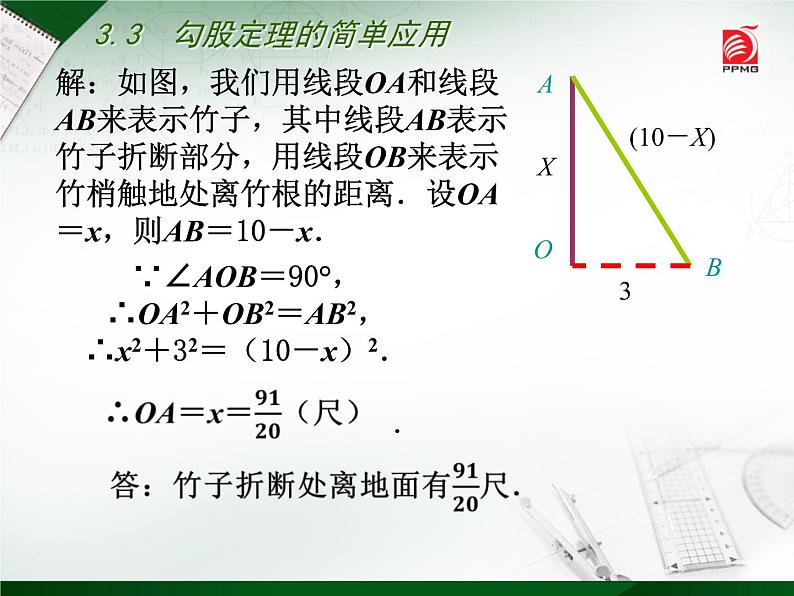
解：如图，我们用线段OA和线段AB来表示竹子，其中线段AB表示竹子折断部分，用线段OB来表示竹梢触地处离竹根的距离．设OA＝x，则AB＝10－x．
∵∠AOB＝90°，∴OA2＋OB2＝AB2，∴x2＋32＝（10－x）2．
　“引葭赴岸”是《九章算术》中另一道题“今有池方一丈，葭生其中央，出水一尺,引葭赴岸，适与岸齐．问水深、葭长各几何？”
　　题意是：有一个边长为10尺的正方形池塘，在水池正中央有一根新生的芦苇，它高出水面1尺，如果把这根芦苇沿与水池边垂直的方向拉向岸边，它的顶端恰好到达岸边．请问这个水池的深度和这根芦苇的长度各是多少？
　　BC为芦苇长，AB为水深，AC为池中心点距岸边的距离．
　　　　　设AB ＝x尺，则BC ＝（ x ＋1）尺，根据勾股定理得： x2＋52＝(x＋1)2，即：（x＋1）2－x2 ＝52，解得：x＝12， 所以芦苇长为12＋1＝13（尺）， 　答：水深为12尺，芦苇长为13尺． 
例2　如图，在△ABC中， AB＝26，BC＝20，BC边上的 中线AD＝24，求AC.
∴BD＝CD＝ BC＝ ×20＝10．∵AD2＋BD2＝576＋100＝676， AB 2＝262＝676，
勾股定理与它的逆定理在应用上有什么区别？
　勾股定理主要应用于求线段的长度、图形的周长、面积； 　勾股定理的逆定理用于判断三角形的形状．
1．如图，在△ABC中， AB＝AC＝17，BC＝16，求△ABC的面积．
2．如图，在△ABC中，AD⊥BC，AB＝15，AD＝12，AC＝13，求△ABC的周长和面积．