高中物理人教版 (新课标)必修2第五章 曲线运动综合与测试优质教学设计

章末分层突破

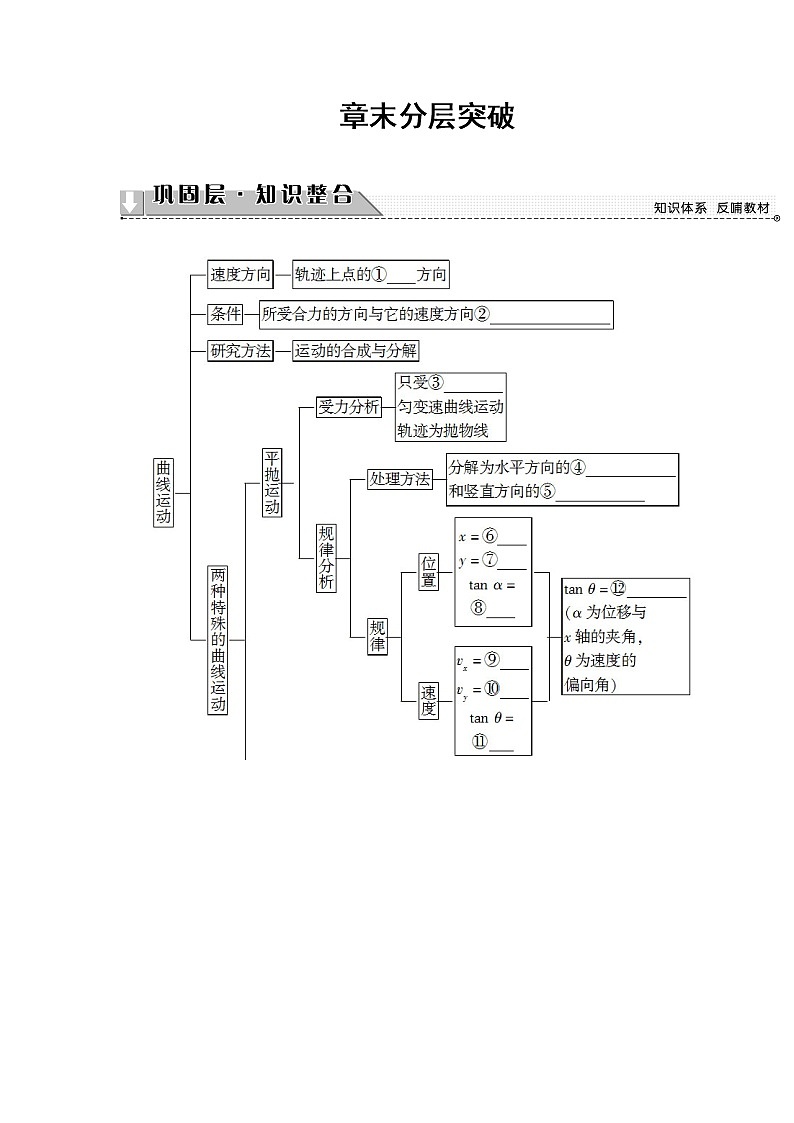
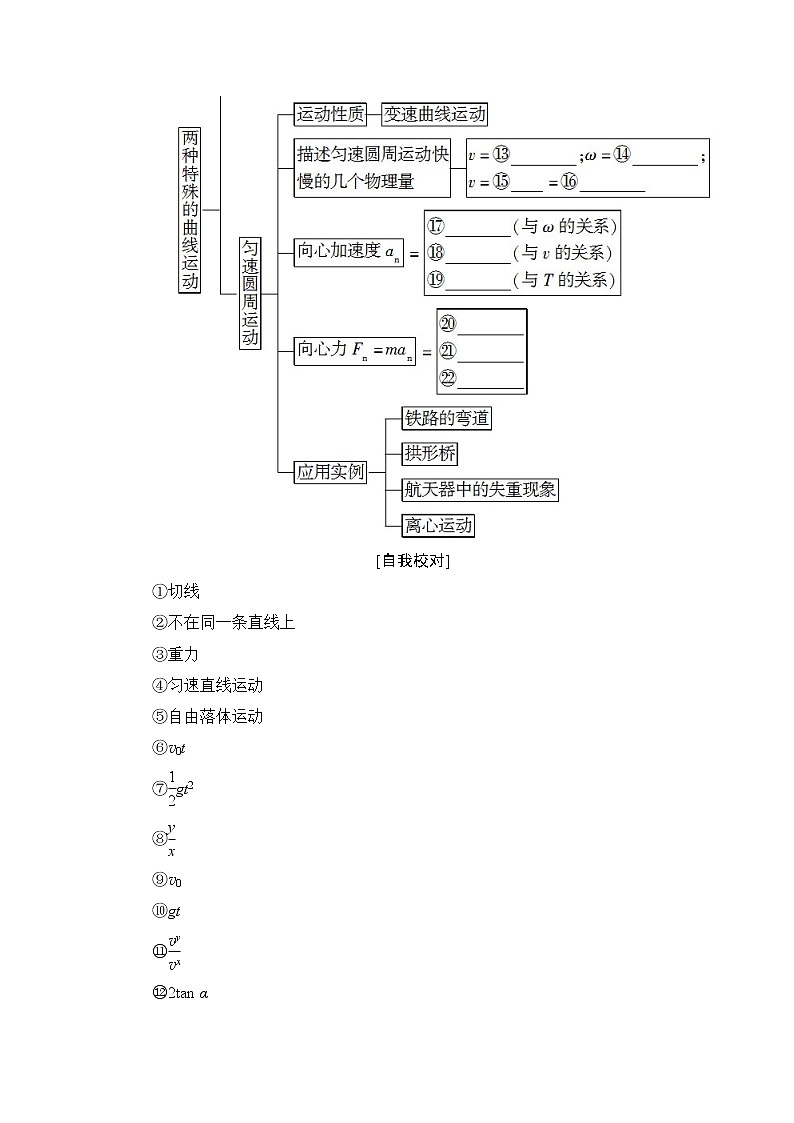
[自我校对]

①切线

②不在同一条直线上

③重力

④匀速直线运动

⑤自由落体运动

⑥v0t

⑦gt2

⑧

⑨v0

⑩gt

⑪

⑫2tan α

⑬

⑭

⑮ωr

⑯

⑰ω2r

⑱

⑲2r

⑳mω2r

m

m2r

　______________________________________________________________

　______________________________________________________________

　______________________________________________________________

　______________________________________________________________

1.小船渡河过程中，随水漂流和划行这两个分运动互不干扰，各自独立而且具有等时性

(1)渡河时间最短问题：只要分运动时间最短，则合运动时间最短，即船头垂直指向对岸渡河时时间最短．

(2)航程最短问题：要求合位移最小．当v水<v船时，合运动的速度可垂直于河岸，最短航程为河宽．当v水>v船时，船不能垂直到达河岸，但仍存在最短航程，当v船与v合垂直时，航程最短．

2．跨过定滑轮拉绳(或绳拉物体)运动的速度分解

物体运动的速度为合速度v，物体速度v在沿绳方向的分速度v1就是使绳子拉长或缩短的速度，物体速度v的另一个分速度v2就是使绳子摆动的速度，它一定和v1垂直．

　(多选)在一次抗洪抢险战斗中，一位武警战士驾船把群众送到河对岸的安全地方．设河水流速为3 m/s，河宽为600 m，船相对静水的速度为4 m/s.则下列说法正确的是(　　)

A．渡河的最短时间为120 s

B．渡河的最短时间为150 s

C．渡河的最短航程为600 m

D．渡河的最短航程为750 m

【解析】　当船速垂直于河岸时，渡河时间最短，t＝＝150 s．当船沿垂直河岸方向行驶时即合速度垂直河岸时，航程最短为600 m，故B、C正确．

【答案】　BC

平抛运动是典型的匀变速曲线运动，它的动力学特征是：水平方向有初速度而不受外力，竖直方向只受重力而无初速度，抓住了平抛运动的这个初始条件，也就抓住了它的解题关键，现将常见的几种解题方法介绍如下：

1．利用平抛运动的时间特点解题

平抛运动可分解成水平方向的匀速直线运动和竖直方向的自由落体运动，只要抛出的时间相同，下落的高度和竖直分速度就相同．

2．利用平抛运动的偏转角解题

设做平抛运动的物体下落高度为h，水平位移为x时，速度vA与初速度v0的夹角为θ，由图5­1可得：tan θ＝＝＝＝              ①

图5­1

将vA反向延长与水平位移相交于O点，设A′O＝d，则有：tan θ＝

解得d＝x，tan θ＝2＝2tan α  ②

①②两式揭示了偏转角和其他各物理量的关系．

3．利用平抛运动的轨迹解题

平抛运动的轨迹是一条抛物线，已知抛物线上的任意一段，就可求出水平初速度和抛出点，其他物理量也就迎刃而解了．设图5­2是某小球做平抛运动的一段轨迹，在轨迹上任取两点A和B，过A点作竖直线，并与过B点作的水平线相交于C点，然后过BC的中点D作垂线交轨迹于E点，再过E点作水平线交AC于F点，小球经过AE和EB的时间相等，设为单位时间T.由Δy＝gT2知

T＝＝，v0＝＝·xEF.

图5­2

　一带有乒乓球发射机的乒乓球台如图5­3所示．水平台面的长和宽分别为L1和L2，中间球网高度为h.发射机安装于台面左侧边缘的中点，能以不同速率向右侧不同方向水平发射乒乓球，发射点距台面高度为3 h．不计空气的作用，重力加速度大小为g.若乒乓球的发射速率v在某范围内，通过选择合适的方向，就能使兵乓球落到球网右侧台面上，则v的最大取值范围是(　　)

【导学号：50152050】

图5­3

A.<v<L1

B.<v<

C.<v<

D.<v<

【解析】　设以速率v1发射乒乓球，经过时间t1刚好落到球网正中间．则竖直方向上有3h－h＝gt　              ①

水平方向上有＝v1t1　 ②

由①②两式可得v1＝

设以速率v2发射乒乓球，经过时间t2刚好落到球网右侧台面的两角处，在竖直方向有3h＝gt　              ③

在水平方向有＝v2t2　 ④

由③④两式可得v2＝

则v的最大取值范围为v1＜v＜v2.故选项D正确．

【答案】　D

1.当物体从某种特性变化为另一种特性时，发生质的飞跃的转折状态，通常叫做临界状态．出现临界状态时，既可理解为“恰好出现”，也可理解为“恰好不出现”．

2．确定临界状态的常用方法

(1)极限法：把物理问题(或过程)推向极端，从而使临界现象显露，达到尽快求解的目的．

(2)假设法：有些物理过程中没有明显出现临界问题的线索，但在变化过程中可能出现临界问题．

3．临界问题经常出现在变速圆周运动中，而竖直平面内的圆周运动是最典型的变速圆周运动．在竖直平面内的圆周运动一般不是匀速圆周运动，但物体经最高点或最低点时，所受的重力与其他力的合力指向圆心，提供向心力．

 (1)用绳子系物体或物体沿轨道内侧运动(如图5­4所示)．

图5­4

此种情况下，如果物体恰能通过最高点，即绳子的拉力或轨道对物体的支持力等于零，只有重力提供向心力，即mg＝，得临界速度v0＝.当物体的速度大于v0时，才能经过最高点．

(2)用杆固定物体在竖直平面内做圆周运动．

此种情况下，由于物体所受的重力可以由杆给它的向上的支持力来平衡，所以在最高点时的速度可以为零．当物体在最高点的速度v≥0时，物体就可以完成一个完整的圆周运动．

　(多选)如图5­5所示，长0.5 m的轻质细杆，一端固定有一个质量为3 kg的小球，另一端由电动机带动，使杆绕O点在竖直平面内做匀速圆周运动，小球的速率为2 m/s.取g＝10 m/s2，下列说法正确的是(　　)

图5­5

A．小球通过最高点时，对杆的拉力大小是24 N

B．小球通过最高点时，对杆的压力大小是6 N

C．小球通过最低点时，对杆的拉力大小是24 N

D．小球通过最低点时，对杆的拉力大小是54 N

【解析】　设小球在最高点时受杆的弹力向上，则mg－FN＝m，得FN＝mg－m＝6 N，故小球对杆的压力大小是6 N，A错误，B正确；小球通过最低点时FN－mg＝m，得FN＝mg＋m＝54 N，小球对杆的拉力大小是54 N，C错误，D正确．

【答案】　BD

　(多选)如图5­6所示为赛车场的一个水平“U”形弯道，转弯处为圆心在O点的半圆，内外半径分别为r和2r.一辆质量为m的赛车通过AB线经弯道到达A′B′线，有如图所示的①、②、③三条路线，其中路线③是以O′为圆心的半圆，OO′＝r.赛车沿圆弧路线行驶时，路面对轮胎的最大径向静摩擦力为Fmax.选择路线，赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变，发动机功率足够大)，则(　　)

【导学号：50152051】

图5­6

A．选择路线①，赛车经过的路程最短

B．选择路线②，赛车的速率最小

C．选择路线③，赛车所用时间最短

D．①、②、③三条路线的圆弧上，赛车的向心加速度大小相等

【解析】　由几何关系可得，路线①、②、③赛车通过的路程分别为：(πr＋2r)、(2πr＋2r)和2πr，可知路线①的路程最短，选项A正确；圆周运动时的最大速率对应着最大静摩擦力提供向心力的情形，即μmg＝m，可得最大速率v＝，则知②和③的速率相等，且大于①的速率，选项B错误；根据t＝，可得①、②、③所用的时间分别为t1＝，t2＝，t3＝，其中t3最小，可知线路③所用时间最短，选项C正确；在圆弧轨道上，由牛顿第二定律可得：μmg＝ma向，a向＝μg，可知三条路线上的向心加速度大小均为μg，选项D正确．

【答案】　ACD

竖直平面内圆周运动的分析方法

(1)竖直平面内的圆周运动一般是变速圆周运动，运动速度的大小和方向在不断发生变化，通常只研究物体在最高点和最低点的情况．

(2)质点在轻杆作用下绕中心点做圆周运动时，在最高点轻杆能提供支持力或拉力．当v＝时，杆的弹力为零，这时杆的作用力是支持力或拉力的分界点；当0<v<时，杆的支持力随速度的增大而减小；当v>时，杆的拉力随速度的增大而增大．在最低点轻杆能提供拉力且拉力随速度的增大而增大．

(3)竖直平面内的圆周运动往往和机械能守恒定律、动能定理及平抛运动结合，此类问题利用机械能守恒定律、动能定理将最高点和最低点的物理量联系起来．

(教师用书独具)

1．(多选)如图5­7所示为赛车场的一个水平“梨形”赛道，两个弯道分别为半径R＝90 m的大圆弧和r＝40 m的小圆弧，直道与弯道相切．大、小圆弧圆心O、O′距离L＝100 m．赛车沿弯道路线行驶时，路面对轮胎的最大径向静摩擦力是赛车重力的2.25倍．假设赛车在直道上做匀变速直线运动，在弯道上做匀速圆周运动．要使赛车不打滑，绕赛道一圈时间最短(发动机功率足够大，重力加速度g＝10 m/s2，π＝3.14)，则赛车(　　)

图5­7

A．在绕过小圆弧弯道后加速

B．在大圆弧弯道上的速率为45 m/s

C．在直道上的加速度大小为5.63 m/s2

D．通过小圆弧弯道的时间为5.58 s

【解析】　赛车做圆周运动时，由F＝知，在小圆弧上的速度小，故赛车绕过小圆弧后加速，选项A正确；

在大圆弧弯道上时，根据F＝m知，其速率v＝＝＝45 m/s，选项B正确；

同理可得在小圆弧弯道上的速率v′＝30 m/s.

如图所示，由边角关系可得α＝60°，直道的长度x＝Lsin 60°＝50 m

据v2－v′2＝2ax知

在直道上的加速度a≈6.50 m/s2，选项C错误；

小弯道对应的圆心角为120°，弧长为s＝，

对应的运动时间t＝≈2.79 s，选项D错误．

【答案】　AB

2．如图5­8所示，帆板在海面上以速度v朝正西方向运动，帆船以速度v朝正北方向航行，以帆板为参照物(　　)

图5­8

A．帆船朝正东方向航行，速度大小为v

B．帆船朝正西方向航行，速度大小为v

C．帆船朝南偏东45°方向航行，速度大小为v

D．帆船朝北偏东45°方向航行，速度大小为v

【解析】　以帆板为参照物，帆船具有朝正东方向的速度v和朝正北方向的速度v，两速度的合速度大小为v，方向朝北偏东45°，故选项D正确．

【答案】　D

3．如图5­9所示为足球球门，球门宽为L.一个球员在球门中心正前方距离球门s处高高跃起，将足球顶入球门的左下方死角(图中P点)．球员顶球点的高度为h.足球做平抛运动(足球可看成质点，忽略空气阻力)，则(　　)

图5­9

A．足球位移的大小x＝

B．足球初速度的大小v0＝

C．足球末速度的大小v＝

D．足球初速度的方向与球门线夹角的正切值tan θ＝

【解析】　根据几何关系可知，足球做平抛运动的竖直高度为h，水平位移为x水平＝，则足球位移的大小为：x＝＝，选项A错误；由h＝gt2，x水平＝v0t，可得足球的初速度为v0＝，选项B正确；对小球应用动能定理：mgh＝－，可得足球末速度v＝＝，选项C错误；初速度方向与球门线夹角的正切值为tan θ＝，选项D错误．

【答案】　B

4．未来的星际航行中，宇航员长期处于零重力状态，为缓解这种状态带来的不适，有人设想在未来的航天器上加装一段圆柱形“旋转舱”，如图5­10所示．当旋转舱绕其轴线匀速旋转时，宇航员站在旋转舱内圆柱形侧壁上，可以受到与他站在地球表面时相同大小的支持力．为达到上述目的，下列说法正确的是(　　)

图5­10

A．旋转舱的半径越大，转动的角速度就应越大

B．旋转舱的半径越大，转动的角速度就应越小

C．宇航员质量越大，旋转舱的角速度就应越大

D．宇航员质量越大，旋转舱的角速度就应越小

【解析】　旋转舱对宇航员的支持力提供宇航员做圆周运动的向心力，即mg＝mω2r，解得ω＝，即旋转舱的半径越大，角速度越小，而且与宇航员的质量无关，选项B正确．

【答案】　B

5．某物理小组的同学设计了一个粗测玩具小车通过凹形桥最低点时的速度的实验．所用器材有：玩具小车、压力式托盘秤、凹形桥模拟器(圆弧部分的半径为R＝0.20 m)．

(a)　　　　　　　　　　(b)

图5­11

完成下列填空：

(1)将凹形桥模拟器静置于托盘秤上，如图5­11(a)所示，托盘秤的示数为1.00 kg；

(2)将玩具小车静置于凹形桥模拟器最低点时，托盘秤的示数如图(b)所示，该示数为________kg；

(3)将小车从凹形桥模拟器某一位置释放，小车经过最低点后滑向另一侧．此过程中托盘秤的最大示数为m；多次从同一位置释放小车，记录各次的m值如下表所示.

(4)根据以上数据，可求出小车经过凹形桥最低点时对桥的压力为________N；小车通过最低点时的速度大小为________m/s.(重力加速度大小取9.80 m/s2，计算结果保留2位有效数字)

【解析】　(2)题图(b)中托盘秤的示数为1.40 kg.

(4)小车5次经过最低点时托盘秤的示数平均值为m＝ kg＝1.81 kg.

小车经过凹形桥最低点时对桥的压力为

F＝(m－1.00)g＝(1.81－1.00)×9.80 N≈7.9 N

由题意可知小车的质量为

m′＝(1.40－1.00) kg＝0.40 kg

对小车，在最低点时由牛顿第二定律得

F－ m′g＝

解得v≈1.4 m/s.

【答案】　(1)1.40　(2)7.9　1.4